In this section we provide an overview of data preprocessing, introduce the TE-CDE25 and finally describe OptAB in detail.
Optimal antibiotic selection by OptAB
OptAB iteratively selects optimal antibiotic treatments by minimizing the SOFA score associated with treatment success while considering drug-related side effects. A reliable assessment of initial treatment efficacy occurs 48 h after administration, during which the treatment should remain unchanged, except for results from microbiological cultures, resistance tests, and laboratory values indicating severe contraindications. After the initial evaluation and any necessary adjustments, efficacy should be reassessed every 24 h9,26,27.
Given the life-threatening nature of sepsis, the primary treatment goal is to combat the infection, thereby reducing the SOFA score. Antibiotic administration should be avoided if contraindicated, and among equally effective treatments, the one with the least side effects should be preferred. Consequently, OptAB iteratively selects the antibiotic (or combination of antibiotics) that minimizes the SOFA score after 48 or 24 h while adhering to specific thresholds for contraindications and side effects.
At each iteration all available measurements are fed into OptAB to obtain updated predictions. OptAB excludes antibiotics with known resistance against pathogens from its treatment optimization. Once a side-effect associated threshold is violated, OptAB raises warnings to identify high-risk patients for antibiotic-associated side-effects and propose alternative treatment options. If the SOFA-Score is decreasing over a period of 48 h, OptAB recommends de-escalating antibiotic treatment according to common guidelines for Sepsis and antibiotic de-escalation9,26.
OptAB provides both an optimal treatment recommendation and predictions of the SOFA-Score and laboratory values indicating contraindications and side-effects for all potential treatments. This provide physicians a more comprehensive assessment of possible treatment options for individual patients.
OptAB is based on the Treatment-Effect Controlled Differential equation (TE-CDE) approach25 and accounts for time-dependent confounding. We extended the TE-CDE to optimize dynamic treatment regimes under a realistic medical setting using real-world patient data.
The original TE-CDE comprises an encoder and a decoder, both modeled as Neural CDEs60. The encoder is trained for short-term forecasts using all observed covariates up to time point t and computes an informative latent disease state, which serves as the initial value for the decoder trained for long-term forecasts. To ensure a balanced representation of the latent disease state61, we incorporate a penalty term for the prediction accuracy of future treatments based on this latent state25. This approach mitigates the time-dependent confounding effects between the latent disease state and future treatments.
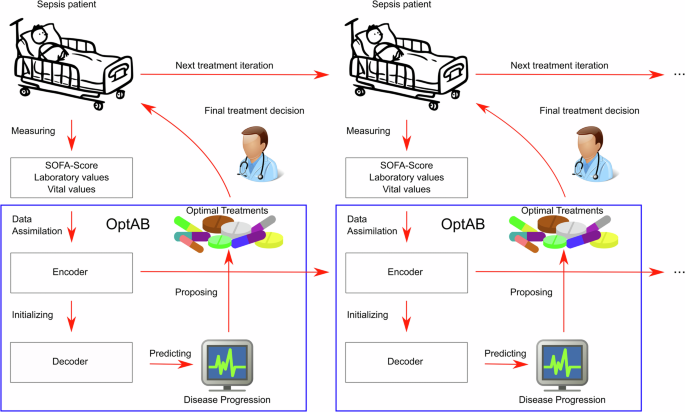
During inference, the encoder assimilates the available data for an individual patient from the past to the present and generates the patient’s latent disease state to initialize the trained decoder. The decoder then forecasts the future disease course, including the SOFA score and laboratory values indicating side effects, under the specified treatment. When new data arrives or the treatment changes, the encoder updates the latent disease state, which subsequently refreshes the decoder’s long-term forecasts (see Fig. 7).
OptAB is based on a TE-CDE25 model consisting of an encoder and a decoder. The encoder assimilates all observed data of a patient until the present time point to create a latent disease state which is used by the decoder as an initial value for long-term forecasts. By comparing the predicted disease courses under different antibiotic treatments, the most efficient treatment with tolerable side effects can be selected.
Datasets
We trained and tested OptAB on the large real-world EHR dataset MIMIC-IV29,30 containing over 450.000 admissions to the Beth Israel Deaconess Medical Center of the Harvard medical School including demographics, laboratory values, vital values, medications and diagnosis data. We tested OptAB on AmsterdamUMCdb containing 23.106 admissions from 2003 to 2016 to the intensive care unit of the Amsterdam University Medical center36.
Legal and ethical considerations
For Mimic-IV, the collection of patient information and creation of the research was reviewed by the Institutional Review Board at the Beth Israel Deaconess Medical Center, who granted a waiver of informed consent and approved the data sharing initiative29,30.
For AmsterdamUMCdb, an internal team carried out a data privacy impact assessment and an external team performed an audit. The external team was led by a member of the privacy expert group at the Netherlands Federation of UMCs. The Regional Medical Ethics Committee confirmed that the creation of AmsterdamUMCdb was not eligible for their assessment as no specific research question was involved. The Ethics in Intensive Care Medicine group provided external ethics review and appraisal36.
Both datasets were shared by the data owners for research purposes upon request and under the supervision of a practicing intensive care physician (Dr. Ingobert Wenningmann) in AmsterdamUMCdb. No further ethical approval was required as no further data was used.
Definition of Sepsis
For SOFA-Score calculation and Sepsis-3 classification adhering to the latest Sepsis-3 criteria56,62 we employed the OpenSep pipeline63 for the MIMIC-IV dataset and the ricu R package for AmsterdamUMCdb64. Patients with a SOFA-Score greater than or equal to 2 occurred within 48 h before or 24 h after a suspicion of infection (SOI) were classified as Sepsis patients. A suspicion of infection is defined as either the administration of antibiotics followed by sampling of bodily fluids for microbiological cultures within 24 h or sampling of bodily fluids for microbiological cultures followed by the administration of antibiotics within 72 h. The onset of Sepsis is the earlier event of sampling for microbiological cultures or the administration of antibiotics.
Data preprocessing
We focussed on patients admitted to the Intensive Care Unit since the SOFA-Score can only be determined using data collected at the ICU and extract all patients treated with Vancomycin, Piperacillin/Tazobactam and Ceftriaxone. To avoid bias from treatment effects of other antibiotics we excluded all patients who additionally received other antibiotics. We modeled the three antibiotics as binary features, because they were typically administered according to standard treatment regimes in our datasets. This enables OptAB to predict the (long-term) effects of antibiotic treatments rather than the (short-term) effects of individual administrations.
Before training of OptAB we performed a variable selection considering all observed laboratory variables and vital parameters as potential time-dependent predictors. We excluded all variables measured in less than 50% of the patients. Then, we calculated the absolute Spearman-correlation between the SOFA-Score and the potential covariables. Due to sparse and highly irregular measurements of the laboratory values and vital signs, we divided the data into 12 h intervals for the calculation of the Spearman-correlation. We selected all variables with an absolute Spearman-correlation of more than 0.3 in at least one time interval. Plots of the Spearman-correlation can be found in our Github repository (https://github.com/philippwendland/OptAB).
The selected time-dependent features are the SOFA-Score, alanine transaminase (in IU/L), anion gap (in mEq/L), bicarbonate (in mEq/L), bilirubin total (in mg/dl), blood urea nitrogen (in mg/dl), creatinine (in mg/dl), diastolic blood pressure (in mmHg), number of platelets (in k/uL), red cell distribution width (in %) and systolic blood pressure (in mmHg). The selected static features are biological sex, age, height and weight at submission.
We included cumulative missing masks as extra variables as the missingness pattern in Electronic Health Records often contains important information about the patient’s state65. These masks describe whether a variable is observed or not60.
Mathematical notation
In this subsection we introduce some basic notations. For each patient i, let \(Z=({z}_{{t}_{0}},{z}_{{t}_{1}},…,{z}_{{t}_{K}})\in {{\mathbb{R}}}^{L\times K}\) be a matrix of the temporal covariates with t0 corresponding to the latest of Sepsis onset or first measured SOFA-Score. Z contains missing values, because the variables are usually measured at different frequencies and times. Let \(A=({a}_{{t}_{0}},{a}_{{t}_{1}},…,{a}_{{t}_{K}})\in {{\mathbb{R}}}^{M\times K}\) be a matrix of the antibiotic treatments with \({a}_{{t}_{j}}^{m}=1\) if the patient is treated at tj with antibiotic m and \({a}_{{t}_{j}}^{m}=0\) otherwise. In our context, treated at tj implies that the treatment is ongoing. Let \(d\in {{\mathbb{R}}}^{D}\) be the static variables. Y ⊂ Z with \(Y=({y}_{{t}_{0}},{y}_{{t}_{1}},…,{y}_{{t}_{n}})\in {{\mathbb{R}}}^{R\times K}\) is the outcome corresponding to the patient’s disease state and side-effects indicating laboratory values.
Neural differential equations
Neural Ordinary Differential Equations (Neural ODEs)66 are a hybrid neural network approach modeling the right-hand side of an ODE as a neural network. Let \({f}_{\phi }:{{\mathbb{R}}}^{P}\to {{\mathbb{R}}}^{P}\) and \({g}_{\varphi }:{{\mathbb{R}}}^{L}\to {{\mathbb{R}}}^{P}\) be neural networks and let \({z}_{{t}_{0}}\in {{\mathbb{R}}}^{L}\) be a vector of covariables measured at t0. A Neural ODE can be defined as
$${x}_{{t}_{0}}={g}_{\varphi }\left({z}_{{t}_{0}}\right),{x}_{t}={x}_{{t}_{0}}+{\int_{{t}_{0}}^{t}}{f}_{\phi }\left({x}_{s}\right)ds$$
(1)
The predictions of standard Neural ODEs are based solely on data measured at t0 and do not incorporate subsequent measurements.
Neural Controlled Differential Equations60 extend Neural ODEs by solving a Riemann-Stieltjes-Integral instead of a classic Riemann-Integral to process subsequent measurements, irregularities and missing values of time series data. Let \({F}_{\theta }:{{\mathbb{R}}}^{P}\to {{\mathbb{R}}}^{P\times \left(L+1\right)}\) and \({g}_{\eta }:{{\mathbb{R}}}^{L}\to {{\mathbb{R}}}^{P}\) be neural networks depending on parameters θ and η. Let \({{\mathcal{X}}}_{Z}:\left[{t}_{0},t\right]\to {{\mathbb{R}}}^{\left(L+1\right)}\) be an interpolation of a time series \(Z=({z}_{{t}_{0}},…,{z}_{{t}_{K}})\in {{\mathbb{R}}}^{L\times K}\) such that \({{\mathcal{X}}}_{Z}({t}_{j})=({t}_{j},{z}_{{t}_{j}})\). A Neural CDE is defined as the solution \(x\left(t\right)\) to
$${x}_{{t}_{0}}={g}_{\eta }\left({z}_{{t}_{0}}\right),{x}_{t}={x}_{{t}_{0}}+{\int_{{t}_{0}}^{t}}{F}_{\theta }\left({x}_{s}\right)\frac{d{{\mathcal{X}}}_{Z}\,\left(s\right)}{ds}ds$$
(2)
Often \({{\mathcal{X}}}_{Z}\) is called driver or control of the Neural CDE. To ensure causality and online-updateability we use the rectilinear interpolation scheme67.
Treatment-effect controlled differential equation (for predicting the disease state of Sepsis patients and antibiotic-associated side-effects)
The TE-CDE25,60 consists of an Encoder and decoder both modeled as Neural Controlled Differential equations. Here we describe the extensions to antibiotic treatment optimization taking side-effects into account (see Fig. 7).
The Encoder is trained for short-term predictions until t + ϵ ≥ t0, where ϵ corresponds to the forecast horizon. The Encoder assimilates all variables Z and treatments A measured up to the current timepoint t.
$${x}_{{t}_{0}}={g}_{\eta }\left({z}_{{t}_{0}},{a}_{{t}_{0}},d\right),{x}_{t+\epsilon }={x}_{{t}_{0}}+{\int_{{t}_{0}}^{t+\epsilon }}{F}_{\theta }\left({x}_{s}\right)\frac{d{{\mathcal{X}}}_{Z,A}\left(s\right)}{ds}ds$$
(3)
The decoder is trained for long-term predictions up to \({t}^{{\prime} }\, >\, t+\epsilon\) and is initialized by a transformation of the latent disease state of the Encoder xt+ϵ at t + ϵ and the static variables d. We set ϵ = 1h for the disease prediction of Sepsis patients
$${x}_{{t}^{{\prime} }}={g}_{\varphi }\left({x}_{t+\epsilon },d\right)+{\int_{t+\epsilon }^{{t}^{{\prime} }}}{f}_{\phi }\left({x}_{s}\right)ds$$
(4)
Although it is possible to drive the decoder by a future treatment scheme A it is not reasonable in our use case, because the efficacy of initial antibiotics can only be evaluated 48 h after treatment and should be re-evaluated every 24 h9,26,27. Therefore, we set the long-term prediction horizon to \({t}^{{\prime} }=t+48h\) or \({t}^{{\prime} }=t+24h\). The decoder requires no control A and is therefore simplified to a standard Neural ODE. If an antibiotic needs to be changed due to contraindications or its efficacy is evaluated at tchange, further observations of the covariables are available. These observations are fed into the encoder to derive an updated latent disease state at tchange + ϵ, which is then used to initialize the decoder.
We use two neural networks \({h}_{\alpha }:{{\mathbb{R}}}^{P}\to {{\mathbb{R}}}^{R}\) and \({h}_{\beta }:{{\mathbb{R}}}^{P}\to {{\mathbb{R}}}^{M}\) to calculate the forecasts of the outputs \({\hat{y}}_{s}={h}_{\alpha }\left({x}_{s}\right)\) and treatment probabilities \({\hat{p}}_{s}=\sigma ({h}_{\beta }\left({x}_{s}\right))\) where σ corresponds to the Softmax activation function.
Time-dependent confounding
One major challenge for estimating counterfactual outcomes with longitudinal observational data is the influence of time-dependent confounders on treatment administration24,68. The presence of confounders can lead to biased causal effect estimations. The Treatment-Effect Controlled Differential Equation penalizes the prediction accuracy of the treatment to obtain a balanced representation of the latent disease state. This counteracts time-dependent confounding25,61,69. Concretely, the Binary Cross Entropy of the treatment prediction is maximized to ensure, that the latent representation x is not predictive of the future treatment administration. Of course, the latent representation is influenced by past treatments.
Training and objective function of the TE-CDE25
First, we trained the encoder to obtain a reliable initialization for the decoder \(x\left(t+\epsilon \right)\). The decoder was trained afterwards. The loss function for the encoder and the decoder consists of the MSE of the outcome prediction \({{\mathcal{L}}}_{y}=\frac{1}{K-{t}_{{\rm{start}}}}\mathop{\sum }\nolimits_{j = {t}_{{\rm{start}}}}^{K}\mathop{\sum }\nolimits_{r = 0}^{R}{({y}_{{t}_{j}}^{r}-{\hat{y}}_{{t}_{j}}^{r})}^{2}\) and the Binary Cross Entropy loss of the treatment prediction \({{\mathcal{L}}}_{a}=\frac{1}{K-{t}_{{\rm{start}}}}\mathop{\sum }\nolimits_{j = {t}_{{\rm{start}}}}^{K}\mathop{\sum }\nolimits_{m = 0}^{M}{a}_{{t}_{j}}^{m}\log ({\hat{p}}_{{t}_{j}}^{m})+(1-{a}_{{t}_{j}}^{m})\log (1-{\hat{p}}_{{t}_{j}}^{m})\). The loss function for the encoder and the decoder is defined as
$${\mathcal{L}}=\frac{1}{n}\mathop{\sum }\limits_{i}^{n}{{\mathcal{L}}}_{y}^{i}+\mu {{\mathcal{L}}}_{a}^{i}$$
(5)
We set tstart = 1 for the training of the Encoder. For the decoder tstart varies between 2 and 119 corresponding to the last time when more than 10 % of the patients are located at the Intensive Care Unit. The parameter μ controls the trade-off between outcome prediction and adjustment for treatment confounding.
Study design and selection of antibiotics
For the optimal antibiotic selection we focus on the three antibiotics Vancomycin, Piperacillin/Tazobactam and Ceftriaxone. The selection of these three antibiotics is based on both medical knowledge and data availability. First, we selected the most frequently administered antibiotics, specifically those administered to at least 5000 among the 26.111 hospitalizations with Sepsis in the MIMIC-IV dataset (see Table 1).
More than 50% (14,795) of all Sepsis patients were treated with Vancomycin. Vancomycin is one of the first-line antibiotics for the treatment of Sepsis and is effective against a broad spectrum of gram-positive pathogens including MRSA31. Unfortunately, Vancomycin is renal toxic and causes many acute kidney injuries32,35. Consequently, the administration of Vancomycin to patients with an impaired kidney function or acute kidney injury should be avoided whenever possible.
Piperacillin/Tazobactam was administered to 5937 (22.7%) and Ceftriaxone to 5389 (20.6%) of the Sepsis patients. Both are commonly recommended for Sepsis treatment9. Unfortunately, Ceftriaxone is hepatotoxic and can cause liver injuries, especially in patients with comprised livers or liver impairments33,34.
Cefepime was administered to 6944 patients and Cefazolin was administered to 5687 patients. Patients treated with Cefazolin had a much lower 90-day mortality rate, indicating that some of the patients might not have suffered from severe Sepsis or that Cefazoline was administered for other purposes, like e.g. cellulitis or other skin infections. Only 133 patients were exclusively treated with Cefepime, which is not sufficient for reliably estimating treatment effects. Therefore, we excluded these two antibiotics from our model.
Identification of contraindications and patients at high-risk for side-effects
We defined thresholds for laboratory values indicating patients at high risk for side-effects and contraindications. Due to Vancomycin’s nephrotoxicity we recommend avoiding treatment with Vancomycin in patients with (at least) stage-1 acute kidney injury or a creatinine value exceeding 2 mg/dl. According to current guidelines35 Stage-1 Acute Kidney Injury was defined as either an increase in creatinine of 0.3 mg/dl within 48 h, or an increase of 1.5 times the baseline creatinine within the previous 7 days or an urine output of less than 0.5 ml/kg/h for 6–12 h. We include the creatinine value itself as a contraindication, because Vancomycin administration should be avoided not only in cases of acute kidney injury, but also in patients with chronic kidney injuries70.
Due to the absence of thresholds indicating hepatotoxic contraindications of Ceftriaxone, OptAB relies on thresholds for discontinuing hepatotoxic drugs in tuberculosis treatment. Treatment with hepatotoxic drugs should be discontinued if the bilirubin total level exceeds twice the upper range (2.4 mg/dl for men and 2.2 mg/dl for women) indicating jaundice and bile duct inflammation, or if the alanine transaminase level exceeds five times the upper range (280 U/L) indicating toxic liver injuries and liver cell damages71,72. These thresholds can be adjusted to meet current guidelines or individual assessments by the physician.
Additionally, we compiled a list of sepsis-associated bacterial pathogens in MIMIC-IV that influence the antibiotic selection of OptAB, ensuring that non-pathogens have no influence on the antibiotic selection process. We focus on samples from abscesses, blood cultures, bronchial washings, bronchoalveolar lavage, sputum, tissue and urine as these are highly associated with Sepsis. The availability of samples from other bodily fluids is limited in MIMIC-IV or their association with Sepsis is negligible. Moreover, we compiled a list of potential fungal and viral pathogens in MIMIC-IV that are frequently associated with Sepsis (see https://github.com/philippwendland/OptAB). Unfortunately, AmsterdamUMCdb does not include microbiological data.
Side effect comparison in Fig. 3
In Fig. 3 we accounted for the different number of patients factually treated with different antibiotics by downsampling. Individual patient characteristics can influence the treatment decision of physicians in observational data. This influence can lead to different characteristics among the patient groups factually treated with different antibiotics. In combination with different numbers of patients receiving each antibiotic (Vancomycin: 241, Ceftriaxone: 199 and Piperacillin/Tazobactam: 58) this could introduce bias. Therefore, we excluded patients treated with multiple antibiotics and then sampled from each of the factual treatment groups with equal probability without replacement. For these sampled patients we used OpAB to simulate treatment with Vancomycin and Ceftriaxone.
Implementation details
We performed a train-, test- and validation split (80%, 10%, 10%) for hyperparameter optimization of OptAB including early stopping. Due to the large training time and memory usage of OptAB, we used a train-test split for the hyperparameter optimization instead of a five-fold cross validation. Training was performed using the PyTorch implementation of Adam and hyperparameter optimization was performed using the Optuna implementation of the Tree-structured Parzen Estimator (Tree-Parzen).
We normalized all variables \({\tilde{z}}_{i,l,{t}_{j}}=\frac{{z}_{i,l,{t}_{j}}-{\rm{mean}}\left({z}_{i,l,{t}_{j}}\right)}{{\rm{std}}\left({z}_{i,l,{t}_{j}}\right)}\), where \({\rm{mean}}\left({z}_{i,l,{t}_{j}}\right)\) and \({\rm{std}}\left({z}_{i,l,{t}_{j}}\right)\) represent the mean and standard deviation for variable l over all patients i and times tj.
Although OptAB can handle missing values over time, OptAB is not able to impute missing values at initialization. Consequently, we performed a K-Nearest-Neighbors (KNN) missing value imputation for the initial values of the covariates73.
Due to the usage of the computationally expensive rectilinear interpolation scheme of the Neural CDEs60 we rounded the timepoints of the covariates to hours, because otherwise we were not able to train and test OptAB as the control matrix becomes very large leading to a massive increase in training time and memory usage.