Coral reef restoration can reduce coastal contamination and pollution hazards

General methodology

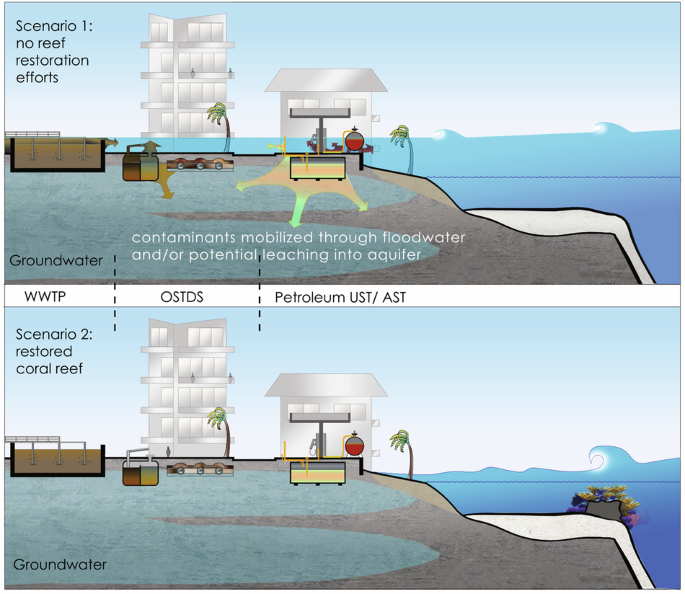
The proposed empirical methodology is derived from an expected damage function approach (EDF)49,85 and uses an interdisciplinary probabilistic risk valuation framework with high-resolution flood modeling36,37,49 (Supplementary Fig. 3). Our study area consists of the coastal areas of the counties Martin, Palm Beach, Broward, Miami-Dade, and the Florida Keys (Upper, Middle and Lower Keys) in Monroe County in Florida.

Datasets and infrastructure elements considered

We downloaded data from five geospatial datasets and considered three types of critical infrastructure elements: we downloaded projected high-resolution (10 m x 10 m) flood extents for different storm return intervals and coral reef restoration scenarios from the U.S. Geological Survey94. We considered registered petroleum storage tanks (pSTs) built in form of underground storage tanks (USTs) with capacity greater than 110 US gal as covered in Chapter 62-761, Florida Administrative Code (F.A.C.), and aboveground storage tanks (ASTs) with capacity greater than 550 US gal as covered in Chapter 62-762, F.A.C. The dataset contains ASTs with tank volumes below the required reporting threshold and we included these as well in our computations, because the exposed location of ASTs to flood waters create a risk for damage and spilling and also tanks with a small volume can cause economic and environmental damage. Stored petroleum-based products considered were different types of gasoline (leaded, unleaded, ethanol E10), diesel (vehicular, emergency generator, and generator pump diesel), aviation fuels (aviation gas and jet fuel), petroleum-based oils (fuel oil/ onsite heat, new/ lube oil, waste oil), drycleaning (drycleaning petroleum, tetrachloroethylene, drycleaning miscellaneous), and other chemical substances (chlorine compound, mineral acid, miscellaneous petroleum-based products and other non-regulated products). Two datasets with information on pSTs were used, one from the Florida Department of Environmental Protection (FDEP) Geospatial Open Data website95, and a second dataset with information on tank contents was provided directly by FDEP.

Furthermore, we considered onsite sewage treatment and disposal systems (OSTDSs) as defined in Section 381.0065(2)(k), Florida Statutes (F.S.), also referred to as septic systems. The dataset was directly provided by FDEP. An individual OSTDS was assumed to have a capacity of 400 US gallon per day. This number is based on the computed average median number of rooms of 4.68 in a housing unit in the five counties of our study96 and the capacity of OSTDSs required for a 4-bedroom residential unit according to 64E-6.008 Florida Administrative Code. We chose to round down to 4 bedrooms to conduct a conservative estimate.

Last, we investigated wastewater treatment facilities, also referred to as wastewater treatment plants (WWTPs) as covered in Chapter 403 F.S. and regulated by the Domestic Wastewater Program and Industrial Wastewater Program by FDEP. The dataset “Wastewater Facility Regulation (WAFR) – Wastewater Facilities” was downloaded from the FDEP Geospatial Open Data website97. The capacity of WTTPs in the study area ranges from 0.0024 MGD to 0.55 MGD. Digital cadastral maps for the five counties of the study area were downloaded from the Florida Department of Revenue98.

Our study represents a conservative approach by assessing the flood contamination risk for pSTs, OSTDSs and WWTPs that are officially registered with the Florida Department of Environmental Protection, respectively, Florida Department of Health. We also assumed a conservative zone of impact of environmental contamination of CIE damage. However, CPCP benefits provided by coral reef restoration for petrochemical exposure could even be higher if further contamination sources of anchored nature (i.e., storage tanks for emergency generators below the threshold) or mobile nature (i.e., petroleum tanks of cars, trucks, boats; portable toilets) were included, and if the radius of the assumed polluted environment is assumed to be larger.

Coral reef restoration specifications and flood scenario development

Storlazzi et al. 49developed models of coastal flooding with current reefs and theoretically restored reefs. The restored coral reef scenario describes a restoration scenario that consists of a solid structure with outplanted live coral top with total vertical height increase of 1.25 m and a cross-shore width of 5.0 m that were situated in water depths between 2 and 7 m on continuous coral/hardbottom habitat and located at the closest point to shore. There are two ways how this could be achieved: (a) either outplanting of tall (mature) live coral, i.e., Acropora palmata, (b) a structural or “gray” restoration with a concrete or metal base structure and juvenile corals rescued from elsewhere or grown in nurseries outplanted on top. Such a base structure in combination with the outplanting of live coral is often referred to as a “hybrid” restoration. Storlazzi et al. (2012b) modeled each of the reef scenarios (current reefs, restored reefs) for 10-year, 50-year, 100-year, and 500-year storm return intervals. Along the study area, per kilometer of coastline, a theoretical reef restoration location was determined based on the bathymetry of the seafloor for depths between 2 and 7 m.

Number of critical infrastructure elements affected and protected from flooding

We determined the number of pSTs, OSTDSs, and WWTPs affected and protected from flooding with a quantitative geospatial analysis in ArcGIS Pro. All locations of CIEs within a distance of 500 m of the largest floodplain (500-year storm return interval, current reefs) were individually verified with Google Maps (satellite imagery), Google Street View, and ArcGIS Pro Imagery Hybrid map to account for spatial inaccuracies. A detailed description of the procedure can be found in the following three subsections.

Number of pSTs

The location of each individual petroleum storage tank within a property corresponding to an address was verified with Google Maps, Google Street View, permit documents and annual inspection reports found at respective links in the FDEP datasets. pSTs located higher than the second story of a building were excluded, since we assumed that flood waters will not reach these storage tank systems. The point layer containing the location of pSTs was intersected with each of the eight floodplain layers. Hereby, the tool spatial join with a radius of 15 m was selected to account for the spatial extent of a storage tank and floodplain uncertainties. For each of the eight flood scenarios, the number of flooded pSTs was calculated.

Number of OSTDSs

The location of OSTDSs as provided in the datasets was at the street level. For each of the flood scenarios, we intersected the polygon layer containing polygons of properties with OSTDSs with each of the floodplains to determine the projected flooded area of the properties. Then, the areas of the flooded space of each property containing an OSTDS was measured for each of the flood scenarios. Subsequently, for each property containing an OSTDS, the spatial ratio \(\alpha\) of flooded property area to total property area was calculated and a spatial cut-off ratio of 20% was used. If α was greater or equal to 20%, it was defined that the OSTDS on that property was flooded. If less than 20% of the property area was flooded, it was defined that the OSTDS was not flooded. We justify a spatial ratio \(\alpha\) of 20%, because on average only a limited area within a property is suitable for an OSTDS to be constructed as there are spatial requirements (open space free of trees, roots, no other built structures on top that could damage the absorption field). Since OSTDSs considered consist of the basic modules of septic tank, absorption field and related piping, by the physical principle of communicating vessels we assume that if one part of an OSTDS is flooded and flood water enters the system somewhere, parts, or even the entire system can become damaged and sewage spills can occur somewhere in the system. Therefore, we considered the use of a ratio \(\alpha\) = 0.2 as the cut-off value, which means one fifth of the property being flooded, a reasonable cut-off value. Based on this computation, for each of the flood scenarios, the state of a particular OSTDS (flooded/not flooded) was determined. The number of OSTDSs flooded for a given scenario was determined by counting the number of properties containing an OSTDS with a spatial ratio \(\alpha \ge\) 20% for a given flood scenario.

Number of WWTPs

The addresses of WWTPs were provided as a point feature class. We verified the location of the property corresponding to an address with Google Satellite Images, and ArcGIS Pro Imagery Hybrid map. We then further refined the WWTP’s spatial extent within a property with information found in official permits, permit construction drawings, and annual inspection reports. A respective link to a FDEP database to access these documents was found for every entry of the FDEP dataset. The WWTP polygon layer was intersected with each of the floodplains and the area of the flooded area within the WWTP was computed. Similar to the OSTDS, the spatial ratio \(\alpha\) of flooded area to total area of the WWTP was calculated. Again, a spatial cut-off ratio of 20% was used to determine the state (flooded/ not flooded) of a WWTP for a given flood scenario.

For each storm return interval, the number of pSTs, OSTDSs, and WWTPs protected from coastal flooding with restored coral reefs was computed as the difference between the number of flooded pSTs for the scenario with current reefs for a given storm return interval, and the number of pSTs with restored reefs for the same storm return interval:

with N being the number of critical infrastructure elements and m being the type of critical infrastructure element (pST, OSTDS or WWTP).

Modeling of damage scenarios and cost functions for petroleum storage tanks and OSTDSs

Based on an online market review (Supplementary Tables 3–5) and a thorough literature search (Supplementary Table 6), we investigated different types of petroleum storage tank and OSTDS damages and failures during wave-driven coastal flooding events, possible contamination scenarios, and necessary environmental remediation actions after a petrochemical or sewage spill. We verified this information by interviews with experts (three certified professional geologists, one industrial hygienist, and one pST manufacturer) that currently work, or have previously worked on projects in the study area (Supplementary Table 7). Based on the information gained, we developed different potential damage scenarios, including damage trees with probabilities and cost functions for flooded pSTs and OSTDSs during wave-driven coastal flooding events. Overall, we considered costs associated with the repair and/or replacement of a pST and costs for environmental remediation after a petroleum product spill. Hereby, based on the information provided in the datasets, we further differentiated between pSTs carrying petroleum product and currently empty pST, to account for the environmental contamination hazard for pST carrying petroleum product (Supplementary Figs. 4–7).

For OSTDSs, we considered the repair and/or replacement of an entire OSTDS or different parts of an OSTDS (septic tank, absorption field), as well as costs for environmental remediation after an OSTDS has leaked and caused a sewage spill. We then created different damage scenarios with decision trees, one for pSTs containing petrochemicals, one for empty pSTs, and one for OSTDS (Supplementary Figs. 8 and 9). To model the costs per damage scenario, we chose PERT distributions with parameters minimum, most likely, and maximum values, as it is suggested in Vose99. The parameters of each PERT distribution were determined based on the extensive literature and market search and verified with interviews with above-mentioned experts. We determined the probabilities of damage and leaking of a flooded petroleum storage tank during a storm event with the help of already mentioned expert interviews in combination with Historical Sea, Lake, and Overland Surges from Hurricanes (SLOSH) simulations of 10 previous hurricanes100,101. A SLOSH simulation is a computational model to simulate storm surges. For OSTDSs, we identified related damage probabilities based on our results found in the literature search and then allocated the estimated damage probabilities to our different possible events in our decision trees. Decision trees for pST and OSTDS damage can be found in Supplemental section are not described here in detail due to a lack of space to include in manuscript.

Modeling of damage scenarios and cost functions for WWTPs

Since WWTPs consist of different components and the spatial extent is larger than for pSTs and OSTDSs, we estimated flood damages based on a damage degree, instead of individual damage scenarios. We used the damage function approach for WWTPs as suggested in Sun et al. 102

which is also used in FEMA HAZUS Flood Modeling for the estimation of direct economic loss to utility system components due to flooding103, and modified it to fit the context of our study. We required modifications, because the WWTPs we considered in this study are smaller than the WWTPs considered in HAZUS104. Hereby, economic damages (US$ loss) for a WWTP are computed as the product of percent of damage (% Damage) and the value of a WWTP. Based on the spatial ratio \(\alpha\) of flooded area to total area of the WWTP that we previously found with the quantitative geospatial analysis, we assumed a corresponding flood depth and percent of damage. For \(\alpha we assumed a flood depth of 0 ft and 0% damage. For \(0.2\,\le \alpha we assumed a flood depth of 1 ft and an assumed damage degree \(\% {Damage}\) = 5%. For \(\alpha =1.0\) we assumed a flood depth of 3 ft and an assumed damage degree \(\% {Damage}\) = 10%. These assumptions can be considered conservative flood depths and damage degrees. We based the value of a WWTP on the average construction costs of a WWTP in dependence of its capacity (Supplementary Fig. 10). For WWTPs with capacity lower than 0.1 MGD, we found construction costs for different biological nutrient removal processes in dependence of different capacities as used by the EPA105. Thereof, we computed average construction costs in dependence of capacity, and with interpolation we determined the value of our WWTPs in dependence of their capacities. For WWTPs of capacity between 0.1 MGD and 0.55 MGD we found the actual average construction costs published106. All found monetary values were converted to 2022 US$.

Assessing economic damages and economic CIE protection and contamination prevention (CPCP) benefits provided by coral reef restoration

For the estimation of economic flood damages and the projection of economic flood protection benefits restored coral reefs can provide, we used Monte Carlo simulations with 1000 iterations (Supplementary Fig. 11). We used two different types of Monte Carlo algorithms, one for the estimation of the present values of damages and CPCP benefits at different scales (per kilometer of coastline, per county, total study area) and one other type for the assessment of damages and benefits projected per storm return interval (10-year, 50-year, 100-year, 500-year). The latter one becomes also relevant for the computation of expected annual damages and benefits (refer to paragraph “Expected annual damages and benefits“ below). The 460 km long coastline was divided into 1 km wide coastal segments.

The algorithm to determine the present values per county and study area is described here. For each iteration, per year (ranging for year 0 to year T (maturity)), we randomly chose a storm of a given storm return interval (10-year, 50-year, 100-year, 500-year; no storm) and corresponding probability of occurrence (1/10; 1/50; 1/100; 1/500; 0.868). We assumed that if a storm hits, every coastal segment of length 1 km along the coast can be affected. For each pST and OSTDS within the flooded region, we chose a random respective damage scenario based on previously determined damage probabilities, and we randomly chose a value for occurring costs based on previously modeled PERT distributions. For WWTPs we used previously determined economic losses based on damage degrees. We then took the occurred damages for each individual CIE and summed up the economic damages per regional scale (per kilometer of coastline; per county; per study area). We repeated this procedure for each year from t = 0 to maturity t = T and discounted each year with a discount rate (see formula below). We then computed the present value of damages \({PV}{\left(D\right)}_{s,c,i}\) and the present value of CIE protection and contamination prevention (CPCP) benefits \(PV{\left(B\right)}_{s,i}\) by summing up over the damages, respective benefits of all T years with

Hereby s is the regional scale (per coastal segment, county, total study area), c is the coral reef restoration scenario (current reefs, restored reefs), i is the number of iteration, t is the time in years from year 0 to T (time of maturity), and r is the discount rate. We used a maturity T of 30 years and a discount rate r of 7% as it is commonly used by FEMA and the U.S. Army Corps of Engineers. The U.S. federal discount rate was reduced from 7 to 3.1% in 2024, thus our results can be considered conservative.

The mean present value of economic damages \({PV}{\left(D\right)}_{s,c}\) describes the flood damages to critical infrastructure that are estimated to occur over a specified period of time, for a specified region, a particular state of coral reef and assumed discount rate. The mean present value of economic CIE protection and contamination prevention (CPCP) benefits (\({PV}{\left(B\right)}_{s}\)) describes the amount of economic damages \({PV}{\left(D\right)}_{s,c}\) over a given time period for a specified region that can be prevented from occurring with a restored coral reef, compared to the present-day state of a coral reef (“current reefs”).

The \({PV}{\left(D\right)}_{s,c,i}\) and \({PV}{\left(B\right)}_{s,i}\) were computed for three different scales: per coastal segment of length 1 km, per county, and for the total study area. We repeated this computation 1000 times (1000 iterations; for clarification: damage scenarios and storm return intervals were randomly chosen based on damage probabilities for each iteration), and then computed the mean and standard deviation over these 1000 iterations to determine the mean \({PV}{\left(D\right)}_{s,c}\), mean \({PV}{\left(B\right)}_{s}\), and corresponding standard deviations for different spatial ranges and coral reef restoration scenarios. All mentioned monetary values were converted, or computed with, 2022 US$.

Expected annual damages and expected annual CIE protection and contamination prevention (CPCP) benefits

Expected annual damages \({{EAD}}_{s}\) are defined as the projected annualized damages for a specified area arising from damaged critical infrastructure and potential spills. We used Monte Carlo simulations to compute expected annual damages and expected annual CPCP benefits. Hereby we modified the above-described Monte Carlo simulation by selecting a specific storm return interval and by shortening the lifetime to only one year. We then used the average value per storm return interval to compute expected annual economic damages and economic protection benefits with trapezoidal integration based on Olsen et al.107:

with s being the scale (coastal segment, county, total study area), i representing the respective storm return interval (10-year, 50-year, 100-year, 500-year). 1/ Ti is the respective annual exceedance probability (1/10, 1/50, 1/100, 1/500). Di represent projected mean damages per respective storm return interval.

For expected annual CPCP benefits coral reef restoration can provide, we computed the difference in predicted mean flood losses between a state with present-day coral reefs and a state with restored coral reefs:

Both expected annual damages and expected annual CPCP benefits were further computed for four additional types of parameters: (1.1) the number of CIE projected to be flooded; (1.2) the number of CIE projected to be protected from flooding; (2.1) the estimated volumes of petroleum products and the capacity of wastewater treatment at flood risk; (2.2) the estimated volumes of petroleum products and the capacity of wastewater treatment projected to be protected from flooding.

Discussion of uncertainties of quantitative geospatial analysis

In our model we assumed that floodplains remain constant over a lifetime T = 30 years. This means we assumed the state of current and restored coral reefs also remains constant, and thus there is no degradation of coral reefs over time. However, future continuous coral reef degradation can occur if coral reefs are not restored and if the threats that killed the reefs in the first place are not mitigated, and this would change the floodplain corresponding to the state of current reefs for a given year. Furthermore, climate change impacts the severity of storm events, and a storm event of certain magnitude and annual exceedance probability can be classified as an event with lower annual exceedance probability (10-year storm can become 5-year storm in the future).

Discussion of uncertainties of Monte Carlo simulation model

There are 6 CIE factors that affect the CPCP benefits per length of coastline: (1) the number of CIEs per coastal segment, which is related to the population density and type of CIE technology of a municipality (i.e., centralized wastewater treatment vs. OSTDS); (2) location of a CIE relative to the wave-driven floodplains; (3) number of storm return intervals for which a CIE is protected, as this affects the present value of CPCP benefits and expected CPCP benefits; (4) type of CIE protected, as there are different repair and/or replacement costs for different types of CIEs; (5) size of CIE affected, as the costs for reparation/replacement of pSTs and WWTPs depend on size; and (6) damage probabilities for a flooded CIE. In summary, the higher the number of CIEs protected from flooding by reef restoration, the higher the number of storm-return intervals for which a CIE is protected, the larger the volume of pSTs or capacity of WWTPs, and the higher the damage probability for a CIE, the higher the CPCP benefits per coastal segment on the benefits side of the benefit-cost-analysis.

We further assumed for our Monte Carlo simulation that either no storm or one storm of a random storm return interval can occur per year. However, as statistics (from NOAA) have shown, there have been years with 2 storm events per year in same location. This would imply that annual damages could be higher because the sum of storm damages of two events per year are likely to be higher than only for one. Since our intention was to conduct a conservative approach, we decided to use only one storm per year.

Another aspect to consider is the spatial extent for which a storm causes coastal flooding. In our model we assumed that if a storm occurs, the entire coastline is affected. We decided to include the total study area, because our intention was to model the distribution of damages and CIE protection and contamination prevention benefits from the perspective of each coastal kilometer along the coastline individually. Based on the analysis of previous Historic SLOSH models100, we are aware that the extent of storms can cause storm surges of different spatial extent. We have experimented with different spatial extents of storms, but instead of presenting the results from multiple models with different assumptions, we focus on the results from the most transparent assumption, i.e., that if a storm occurs, the entire coastline is affected.

Our results of the present value of damages and the present value of CPCP benefits show a high standard deviation. This can be explained, because the storm of certain storm return intervals are randomly selected based on given probabilities. If one compares one run of a Monte Carlo simulation in which one 500-year and one 100-year storm occurs, and another run in which only two 10-year storms occur, it can be seen that the sum of damages differs. Also relevant is the year the storm of a given storm return interval occurs, as there are discounting effects. However, this result visualizes very well the reality: if no storm event occurs, the coastal protection function of a coral reef is not required. However, if a storm event with coastal flooding occurs, damages occur within the short time frame of a couple hours to days, and economic damages can be several million to tens of millions of dollars. In these situations, the coastal protection function of a coral reef is strongly beneficial.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.