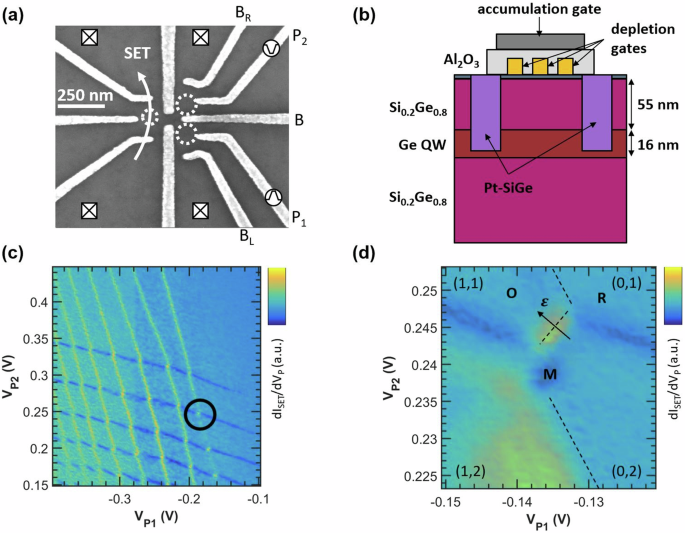
A scanning electron microscope image of the device studied is shown in Fig. 1a along with the Ge/SiGe heterostructure and metal gates in Fig. 1b. The strained Ge quantum well is 16 nm in width and located 55 nm below the surface. For more details regarding the heterostructure, see ref. 5. A two-dimensional hole gas is first created in the Ge well by applying a negative voltage to a global top gate situated above the heterostructure. The double quantum dot (DQD) is then formed underneath plungers P1 and P2 by applying appropriate voltages to the neighboring barrier gates, where the middle barrier voltage VB controls the coupling between the two dots. Varying the plunger voltages controls the chemical potential of each dot, allowing us to reach the few-hole regime (Fig. 1c), where all experiments were performed at the (1,1)-(0,2) anticrossing (Fig. 1d). The hole occupation of both dots was detected by the nearby SET (left half of the device) labeled in Fig. 1a. For convenience in describing this DQD system, we define the relative energy of the two quantum dots as the detuning ε = eα2VP2 − eα1VP1 where αi converts the voltage applied to Pi to the change in the energy levels between the two dots. Figure 1d illustrates the detuning axis on the stability diagram, where we define ε = 0 at the (1,1)-(0,2) boundary.
a SEM image of lithographically defined gates identical to the device used in this study. b Heterostructure of the device showing the Ge quantum well packed between two Ge rich SiGe layers. Ti/Au depletion gates are deposited on top along with an Al global accumulation gate. c A typical stability diagram with the circle highlighting the (1,1)-(0,2) anticrossing. d All experiments were completed at the (1,1)-(0,2) anticrossing, where (n,m) denotes the hole occupation for each dot. Point R was used to reset the DQD, M for measurement and initialization, and O for coherent operation between the singlet and triplet states.
When the system passes the ε = 0 detuning line into the (1,1) charge configuration, the (0,2) singlet state hybridizes with the (1,1) singlet due to the tunnel coupling between the quantum dots: \(\left\vert S\right\rangle =\sin \left(\Omega /2\right)\left\vert {S}_{02}\right\rangle -\cos \left(\Omega /2\right)\left\vert {S}_{11}\right\rangle\). Here, \({\scriptstyle\Omega} =\arctan \left(\frac{2\sqrt{2}{t}_{c}}{\varepsilon }\right)\) is the mixing angle between the two singlet states. In addition to \(\left\vert S\right\rangle\), Fig. 2c depicts the three triplet states that compose the four lowest energy levels in the (1,1) charge configuration. A simple block magnet situated near the device’s PCB provided the field necessary to lift the degeneracy of the three triplet states, generating an estimated fixed global out-of-plane field of 1.2 mT and in-plane field of 4.4 mT measured at the device’s position (∣B∣ = B = 4.6 mT points θ = 15° out of the x-y plane). This tilted field differs from previous qubit experiments on this heterostructure where B was completely in-plane, allowing for a unique perspective into the hole spin states3,11. Importantly, this magnetic field splits the polarized triplet \(\left\vert T\_\right\rangle\) from \(\left\vert {T}_{0}\right\rangle\) by the average Zeeman energy of the quantum dots \({\overline{E}}_{z}\).
a The SET signal as a function of the detuning and evolution time, illustrating coherent oscillations between \(\left\vert S\right\rangle\) and \(\left\vert T\_\right\rangle\). The chevron pattern located near 1 meV arises from the S − T_ anticrossing defined by the energy splitting ΔST_, while oscillations at large detunings are controlled by the average Zeeman energy of the two dots: \({\overline{E}}_{z}\). b Fourier transform of the coherent oscillations in (a), illustrating the S − T_ energy splitting as a function of detuning. c Energy levels (not to scale) of the singlet and triplets as a function of detuning. The Ramsey pulse used is shown below as a function of time and detuning. d Bloch sphere depicting the two rotation axes for the S − T_ subspace. When εP is at the S − T_ anticrossing, the system undergoes X rotations (red axis). For large detunings, a combination of X and Z rotations are performed (blue).
Beginning at M in Fig. 1d, the system is first initialized into the (0,2) singlet state. A voltage pulse was then applied to P1 and P2 to quickly separate the holes and create a small admixture between the (1,1) singlet \({\scriptstyle\left\vert S\right\rangle} =\frac{1}{\sqrt{2}}(\left\vert \uparrow \downarrow \right\rangle -\left\vert \downarrow \uparrow \right\rangle )\) and polarized triplet \(\left\vert T\_\right\rangle =\left\vert \downarrow \downarrow \right\rangle\) states. Once the holes were separated, the system was pulsed to various operation detunings εP and allowed to evolve for a time tE between \(\left\vert S\right\rangle\) and \(\left\vert T\_\right\rangle\) (Fig. 2a, c). We use εP to refer to the change in detuning applied by the pulse, which is offset from ε by the readout position (εr) at point M: ε = εP + εr. The qubit frequency (Fig. 2b) is given by the energy difference between these two states at the operation detuning: hf = ΔEST_, which plateaus to roughly \({\overline{E}}_{z}\) for large detunings.
For smaller operation detunings, the energy splitting reaches a minimum at the S − T_ anticrossing, where it approximately equals 2ΔST_. We define ΔST_ as the coupling between \(\left\vert S\right\rangle\) and \(\left\vert T\_\right\rangle\) at the S − T_ anticrossing. By varying the operation detuning εP from 0.5 to 2.5 meV, we sampled the energy splitting between the two lowest states for both regimes. The existence of this minimum leads to the observed chevron pattern at 1 meV in Fig. 2a, which has been seen in previous S − T_ works and absent from studies coherently manipulating the S − T0 states2,6,7,8,9,10,11.
To understand these dynamics, we utilize a Hamiltonian describing the \(\{\left\vert S\right\rangle ,\left\vert T\_\right\rangle \}\) subspace that was derived in ref. 12 and is a reduced form of the full model used in ref. 9. To leading order, it takes the following form:
$$H=\left(\begin{array}{cc}-J(\varepsilon )&\Delta \\ \Delta &-{\overline{E}}_{z}\end{array}\right).$$
(1)
We define the exchange energy \({\scriptstyle{J}(\varepsilon)}=-\frac{\varepsilon}{2}+\sqrt{\frac{{\varepsilon }^{2}}{4}+2{t}_{c}^{2}}\) as the energy difference between \(\left\vert S\right\rangle\) and \(\left\vert {T}_{0}\right\rangle\). The coupling of the S − T_ states (Δ) emerges from two sources: a spin-flip tunneling process induced by the spin-orbit interaction (Δso) and the anisotropy of the g-tensors (ga) that is primarily determined by the difference of in-plane g-factors: \(\Delta =| {\Delta }_{so}\sin \left(\frac{\Omega }{2}\right)+{g}_{a}{\mu }_{B}B\cos \left(\frac{\Omega }{2}\right)|\)9,12. The anisotropy between the in- and out-of-plane g-factors of a quantum dot has been previously observed, where the in-plane g-factors (g∥) were measured to be a few tens to hundreds of times smaller than their out-of-plane counterparts (g⊥) for holes in Ge/SiGe substrates9,13. The \(\left\vert T\_\right\rangle\) state splits from \(\left\vert {T}_{0}\right\rangle\) by the average Zeeman energy, \({\overline{E}}_{z}=\overline{g}{\mu }_{B}B\), where \(\overline{g}\) is the average g-factor of the two dots projected onto the axis of B.
With this Hamiltonian, we can solve for the frequency of the S − T_ evolution: \({\scriptstyle{f}}=\frac{1}{h}\sqrt{{(J-{\overline{E}}_{z})}^{2}+{(2\Delta )}^{2}}\). At the S − T_ anticrossing, \(J={\overline{E}}_{z}\), and f is controlled by Δ, where X rotations are performed around the Bloch sphere (Fig. 2d). For large detunings, J → 0, leaving f to be determined by the average Zeeman energy and S − T_ coupling, and the qubit rotates near the z axis. The larger the ratio \(\frac{{\overline{E}}_{z}}{\Delta }\) becomes, the closer this axis aligns with the z direction. We note that with control over the orientation of the magnetic field, it is possible for Δ → 0 at specific detunings, resulting in perfect Z rotations12.
After manipulation, the separated holes were reunited in the (0,2) charge configuration at M for spin readout of the final state using Pauli spin blockade. The system is then reset at R before repeating the cycle again. For a detailed explanation of each step of the pulse, see the Supplementary Material.
Dephasing and relaxation
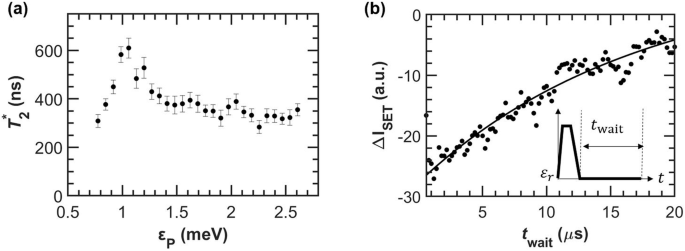
We first analyzed the dephasing and relaxation of this qubit by measuring \({T}_{2}^{* }\) and T1. For each εP in Fig. 2a, the S − T_ evolution was fit to a Gaussian damped sinusoid \(P=A{e}^{-{(t/{T}_{2}^{* })}^{2}}\cos (\omega t+B)+C{e}^{-t/D}+E\), where \({T}_{2}^{* }\) is the inhomogeneous dephasing time. For example traces and details relating to this fit, see the Supplementary Material. After extracting \({T}_{2}^{* }\) as a function of εP (Fig. 3a), a clear dependence on the pulse height is seen. This behavior can be understood with a simple model describing the influence of charge and magnetic noise on the fluctuations in the energy difference between the two states2,6:
$$\sqrt{2}\hslash {T}_{2}^{* -1}=\sqrt{\langle \delta {E}^{2}\rangle }.$$
(2)
a \({T}_{2}^{* }\) as a function of detuning. Linecuts in Fig. 2a are fit to the curve \({P}={{A}{e}^{-{(t/{T}_{2}^{*})}^{2}}}{\rm{cos}} ({{\omega}{t}+{B}})+{{C}{e}^{-t/D}+E}\), where the dephasing time \({T}_{2}^{* }\) is extracted and plotted in (a). Error bars equal one standard deviation of the uncertainty in \({T}_{2}^{* }\) from this fit. This decoherence can be understood as a contribution from two noise terms with the simple model shown in Eqn. (2). From this model, we estimate δΔrms = 0.8 and \(\delta {\overline{E}}_{z,\text{rms}}=3\) neV. b A T1 measurement where the change in SET current is recorded as a function of wait time at the measurement point M. We extract T1 from the fit \(P=A{e}^{\left(-t/{T}_{1}\right)}+B\) (solid line) and calculate T1 = 17.2 ± 3.2 μs. Inset: the pulse used to observe this decay.
At the S − T_ anticrossing where the qubit frequency reaches a minimum, the system is insensitive to first-order to fluctuations in ε due to charge noise. This protection leads to the maximum in \({T}_{2}^{* }\) seen at 1 meV in Fig. 3a. However, the qubit is still susceptible to electrical noise affecting the dot g-factors and tunnel coupling as well as magnetic noise afflicting B. We can estimate the magnitude of this noise combination from Eqn. (2) using the fact that \(J={\overline{E}}_{z}\) at this detuning. Under this condition δE = 2δΔrms, where we define δΔrms to include the noise sources pertinent to tc, ga, and B, leading to
$$\delta {\Delta }_{{\rm{rms}}}\approx \frac{\sqrt{2}\hslash }{2}{({T}_{2}^{* } = 600\text{ns})}^{-1}=0.8\text{neV}.$$
For large operation detunings, the energy separation between the S − T_ states reaches a parallel regime (Fig. 2b), which diminishes the charge noise contribution to δE. In this regime, ΔEST_ approximately equals \({\overline{E}}_{z}\), where the combined electrical and magnetic “Zeeman” noise affecting \(\overline{g}\) and B limits \({T}_{2}^{* }\). We estimate this parameter using Eqn. (2) again:
$$\begin{array}{ll}\delta {E}\,\approx\, \delta {\overline{E}}_{{z},{\text{rms}}},\\ \delta {\overline{E}}_{z,{\text{rms}}}\,\approx\, \sqrt{2}\hslash {({T}_{2}^{* } = 317{\text{ns}})}^{-1}=3{\text{neV}}.\end{array}$$
In general, the T1 spin relaxation time is known to be orders magnitude longer than \({T}_{2}^{* }\) in Ge-based semiconductor QDs at the operation point1,3,14, and we believe this system is similarly limited by \({T}_{2}^{* }\). However, to determine adequate integration times for the projective measurement at the (2,0) readout point εr, the system’s T1 at εr was measured by varying the wait time at εr (Fig. 3b). For these measurements, the system was allowed to completely dephase at the operation detuning εP before being pulsed back to the readout window for a variable amount of time (see inset of Fig. 3b). We fit the resulting exponential decaying curve shown in Fig. 3b to \(P=A{e}^{-(t/{T}_{1})}+B\) and find T1 to be 17.2 ± 3.2 μs, which is comparable to experiments done in S − T0 qubits2.
Gate modulation of the singlet-triplet frequency
We now focus on modulating the coherent evolution of the S − T_ states by adjusting the voltage applied to the barrier separating the two quantum dots. Over a 22 mV range in voltage, Fig. 4 illustrates the dramatic transformation the S − T_ oscillations undergo. As the middle barrier voltage VB is increased, the S − T_ oscillation frequencies undergo an interesting shift seen in Fig. 4. The frequencies in the entire detuning span decrease from VB = −60 mV to −48 mV before oscillations are no longer visible at VB = −46 mV. However, as VB is continuously pushed to more positive values past VB = −46 mV, the oscillations return and now increase with VB. From the Fourier transform of these oscillations, we can isolate two quantities of interest, namely \(\overline{g}\) from the frequency at large detuning following \(f \sim {\overline{E}}_{z}/h\) and ΔST_ from the minimum frequency near εP = 1 meV, where f = 2ΔST_/h.
a–n The upper panel depicts S − T_ oscillations, while the lower panel shows their corresponding FFTs. Applying a more positive barrier gate voltage decreases the frequency of the oscillations throughout the entire detuning range until VB = −46 mV. Afterwards, the frequencies reverse direction and increase. The minimum and maximum frequencies correspond to ΔST_ and \(\overline{g}\).
We would like to note that the location of the frequency minimum ε* is determined by the tunnel coupling tc and \({\overline{E}}_{z}\) from the condition \(J={\overline{E}}_{z}\)9:
$${\varepsilon }_{* }=\frac{2{t}_{c}^{2}-{\overline{E}}_{z}^{2}}{{\overline{E}}_{z}},$$
(3)
Because ε* remains approximately constant throughout this range of VB, a decrease in tc must be accompanied by a decrease in \({\overline{E}}_{z}\). While it is evident from the sharper rises seen in the FFTs of Fig. 4 that tc changes with VB, a similar change in \({\overline{E}}_{z}\), and therefore \(\overline{g}\), is necessarily present. The existence of this minimum frequency marking where \(J={\overline{E}}_{z}\) also serves the purpose of justifying \(J at larger detunings. In this regime, the average Zeeman energy plays the major role in determining the S − T_ evolution frequency. Therefore, we can use the frequency at large εP in Fig. 4 to extract the dependence of \(\overline{g}\) on VB.