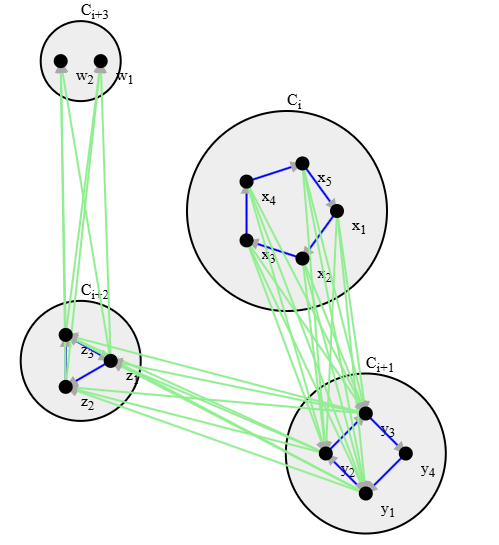
This image illustrates a key step in my Seymour Second Neighborhood Conjecture (SSNC) proof: the Weak Decreasing Exteriors Lemma. We start with a pentagon, which reduces to a square, then a triangle, and finally, a graph with no possible 2-node cycles.
To understand this, imagine an oriented graph (directed, no two-way edges) where we seek a degree-doubling node. I partition the graph into "containers" based on a minimum degree node (not shown), which you see here. These containers are well-ordered and split a node's degree into interior (blue) and exterior (green) neighbors.
This lemma proves the containers shrink in size. With verified assumptions (later proven in the paper), this becomes a crucial building block for proving the conjecture.
Data Source: https://arxiv.org/html/2501.00614
Tools Used: D3.j3
Posted by mindaftermath
3 comments
Yeah nobody knows what this means, bud. I’m sure it’s interesting, but your description is basically jargon to the layman.
Well, the main thing to that from this image is that the containers (the large circles) decrease in size. Sorry that I didn’t make that clear in the OP.
It is like I want to say something about it, but I can’t unless I want to say something even more confusing or point out that your “proven” blue text link should be double-checked.
Comments are closed.