Nonlinear stochastic and quantum motion from Coulomb forces

A pair of equally charged particles of masses mi, i ∈ {1, 2}, confined to a three-dimensional harmonic trap and interacting via the Coulomb potential, can be arranged along the z-axis by having a much greater trap frequency in that direction15,20,21. The axes can then be chosen so that the equilibrium points are \({{{{\bf{d}}}}}^{(i)}=\left(\begin{array}{ccc}0&0&{z}_{i,0}\end{array}\right)\). Even beyond the harmonic approximation, where the motional axes are not decoupled, the interactions depend upon the distances between the two particles along the respective axes. If motion along the x and y axes is sufficiently cooled so that fluctuations along these axes are small, then the interactions between x or y, and z are suppressed. The Hamiltonian of the system can then be written as

where ωi are the trap frequencies, κ = q1q2/4πϵ0 is the coupling strength of the reciprocal interaction calculated via the charge qi and the electric permittivity in vacuum ϵ0, and d = z1,0−z2,0 is the initial distance between the particles’ equilibrium positions. The setup is illustrated in Fig. 1a. In the harmonic approximation, expanding around the distance between the particles in each direction to second order, results in an extra displacement term in the z direction for both particles. The motion of the charged particles is then described by harmonically coupled oscillators with modified frequencies. The coupling induced between the particles is intramodal, such that the modes along different axes do not talk to each other. The third-order term introduces nonlinear and intermodal interactions. To isolate them, a compensating force eliminating the lower-order contributions is necessary. The constant force can be compensated via linear tilt through an electrostatic force41, whereas the linear force can be compensated by parametric control, such as feedback42,43,44. In the regime of optimal compensation, assumed throughout the manuscript, the still reciprocal interaction Hamiltonian can be approximated as

A non-optimal compensation still results in the non-reciprocal nonlinear effect, albeit reduced in visibility, see Supplementary Material (SM) Note 3. Due to the nonlinearity of the Coulomb force, a reciprocal cubic interaction emerges along the z-axis. This is a minimal model of the nonlinear Coulomb interaction between two particles. While similar nonlinear interactions can be constructed for ions directly via the trap geometry for hybrid radial and axial modes39,40, here the nonlinearity emerges directly from the Coulombic interaction between the particles. Both the trap and the compensation operate in the harmonic approximation, and therefore cannot contribute to the nonlinear effects outlined below. Differently than for optical cubic potentials45, the interaction in Eq. (2) combines competing cubic nonlinearities. That is, the cubic single particle potential \({z}_{1}^{3},\,{z}_{2}^{3}\), and the cubic interparticle potential \({z}_{1}{z}_{2}^{2},\,{z}_{1}^{2}{z}_{2}\). Their vying nature may limit the direct observation of the interparticle nonlinear noise or uncertainty-induced phenomena. Quantisation can be accomplished by promoting the canonical variables to operators satisfying the commutation relations [zi, pi] = i.

Fig. 1: Noise and uncertainty-induced momentum displacement via a nonlinear Coulomb interaction.

a(i), (ii) Illustration of the principle in classical and quantum regimes. Two harmonically confined particles (blue, yellow) experience a nonlinear Coulomb interaction (red spring) along a single axis, together with a compensating force (green). In the classical regime, the stochastic particle 1 is prepared in oscillator equilibrium states via dissipation to the thermal environment at temperature T1, while particle 2 is initially cooled to \(T^{\prime} =10\) mK in a room temperature environment T1 = T2 = 300 K. In the quantum regime, the particles are prepared in ground states, and the only fluctuations arise from the quantum uncertainties. A weak linear damping with a rate Γ, acting only on particle 2, is present in order to ensure the stability of the effect. The trap frequency modulation, and mass disproportion of particle 1, as shown in the table, are used to generate unidirectional flow of fluctuations to particle 2, thus avoiding backactions. b(i), (ii) Time evolution of mean momentum \(\langle {p}_{{z}_{2}}\rangle\), normalised to the initial standard deviation (top) and signal-to-noise ratio \({{{{\rm{SNR}}}}}_{{p}_{{z}_{2}}}\) (bottom). For large noise (full circles), the \({{{\rm{SNR}}}}=1/\sqrt{2}\) is quickly reached by all regimes, but tuning frequency (blue) allows for better noise control. At lower noise (empty circles), the parametric symmetry is the only regime reaching the SNR bound (grey). In the quantum regime (b(ii)), the ground state fluctuations (empty circles) are equally harnessed by all regimes, whereas an initial uncertainty amplification, by free-fall (full circle), allows the SNR bound to be reached by all regimes. Symmetric (grey) and tuning frequency (blue) further experience the faster uncertainty growth (SNR drop), not visible for tuning mass (orange), which is also the best regime here.

Classical noise-induced momentum

Nonlinear interactions such as \({z}_{1}^{2}{z}_{2}\) allow for the possibility to coherently displace the momentum of one particle via increases in the initial position noise of the other. Heuristically, the complete reciprocal interaction term of Eq. (2) indicates that for initially uncorrelated states the mean momentum displacement in one mode is rapidly driven by the noise in the other i.e. \(\langle {p}_{{z}_{2}}\rangle \approx \langle {p}_{{z}_{2},0}\rangle -3\kappa (\langle {z}_{1,0}^{2}\rangle -2\langle {z}_{2,0}\rangle \langle {z}_{1,0}\rangle +\langle {z}_{2,0}^{2}\rangle)t/{d}^{4}\). The reciprocal nature of the interaction Hamiltonian of Eq. (2) suggests that a separate asymmetrical manipulation performed solely on one of the two particles can enhance the interparticle non-reciprocal noise-induced nonlinear effect observed on the other. For parametrically symmetric interactions, m1 = m2 and ω1 = ω2, the minimal asymmetrical manipulation is accomplished by unbalancing the initial distribution of thermal noise. That is, prepare the initial thermal state at temperature T = 300 K of particle 2 at an effective temperature of \(T^{\prime} =10\) mK by cooling, while particle 1 is prepared in an oscillator thermal-equilibrium state at room temperature T1 = 300 K. These are zero-mean Gaussian states with variances in position \({\sigma }_{z}^{2}={k}_{B}T/m\omega\) and momentum \({\sigma }_{p}^{2}=m{k}_{B}T\), where T is the effective temperature of mode z and kB is the Boltzmann constant. During the dynamics, the modes are immersed in thermal environments with T1, T2 = 300 K. This initial thermal distribution imbalance between T1 and \(T^{\prime}\) minimises the thermal fluctuations \(\langle {p}_{{z}_{2},0}^{2}\rangle\), which otherwise obscure the noise-induced effect, while simultaneously minimising any unwanted back-action effects on the particle whose noise drives the noise-induced effect. While the technical details of this preparation depend strongly on the chosen platform, we suggest a proof-of-principle state preparation scheme in SM Note 4.

In Fig. 2a we show the noise-induced motion for this parametrically symmetric case (grey). The classical simulations are carried out with the parameters ωi = 50 kHz, m1 = m2 = 8 × 10−17 kg, κ = 2.3 × 10−24 N m2, and d = 3 μm, inspired by optical levitation15,20,21,32 and enriched with magnetic levitation16,17 platforms in mind as they operate with a wider trapping frequency range. No displacement occurs in z1, however, the noise grows rapidly. The mean momentum of the second particle, however, experiences a positive sharp increase away from zero as well as an increase in noise. This displacement is not critically outperformed by noise, as seen in the SNR in Fig. 1b(i) (empty circles). This is a sign of a direct noise-induced coherent effect. Importantly, the SNR grows with increasing \({\sigma }_{{z}_{1,0}}\) (full circles) and can saturate the maximum of \(1/\sqrt{2}\) at the cost of large noise in the initial position of z1.

Fig. 2: Analysis of the time evolution of variables undergoing nonlinear motion.

Analysis of the time evolution of position z1 and momentum \({p}_{{z}_{2}}\) at different initial fluctuations of z1. The shaded area represents the standard deviation around the mean evolution (solid). All quantities are normalised to the standard deviation of their respective initial states. Symmetry breaking by mass tuning (orange) and frequency tuning (blue) allows to control divergence in \({p}_{{z}_{2}}\) in both mean and standard deviation. In the classical regime (a), the mass tuning visibly performs better than the other strategies as it produces larger momentum drift \(\langle {p}_{{z}_{2}}\rangle\). For the quantum regime (b), the symmetric (grey) and frequency tuned (blue) outperform the mass tuned with the same metric. It confirms the result presented in Fig. 1b(i), (ii).

This effect can be explained by examining the Langevin equations of motion for the third-order Coulomb term. These are given by

where Γ is the drag coefficient whose value and phenomenological origin depends upon implementation, and ξ1, ξ2 are independent zero-mean Gaussian white noises with \(\langle {\xi }_{i}({t}^{{\prime} }){\xi }_{i}({t}^{{\prime\prime} })\rangle =\delta ({t}^{{\prime} }-{t}^{{\prime\prime} })\). In what follows, we focus on the underdamped regime, with Γ = 10−4 Hz, as in the overdamped regime, the nonlinear effect in momentum \({p}_{{z}_{2}}\) is not visible (see SM Note 1). For parametric symmetry, it is useful to discuss the dynamics using the mean value approximation, by reducing the two-body interaction into a one-body problem by virtue of the effective potentials \(\tilde{V}({z}_{2})=-3\kappa {\langle {z}_{1}\rangle }^{2}{z}_{2}/{d}^{4}+{\tilde{\omega }}_{2}{z}_{2}^{2}-\kappa {z}_{2}^{3}/{d}^{4}\) and \(\tilde{V}({z}_{1})=3\kappa {\langle {z}_{2}\rangle }^{2}{z}_{1}/{d}^{4}+{\tilde{\omega }}_{1}{z}_{1}^{2}+\kappa {z}_{1}^{3}/{d}^{4}\). In this framework, the unwanted back-action of z2 on z1 is understood as the mean displacement 〈z2〉 which (i) generates a drift in z1, as visible from the first term in \(\tilde{V}({z}_{1})\), and (ii) modifies the frequency of the harmonic confinement of z1 via \({\tilde{\omega }}_{1}={m}_{1}{\omega }_{1}^{2}/2-3\kappa \langle {z}_{2}\rangle /{d}^{4}\). The imbalance in the initial noise properties minimises both back-action contributions at short transients t \(T{\prime}\) makes the noise-induced shift generated by the cubic potential in \(\tilde{V}({z}_{2})\) negligible, keeping the position below the critical value of 〈z2〉 ≈ 1 μm (calculated for the parameters used in numerical simulation) after which the effective frequency \({\tilde{\omega }}_{1}\) becomes negative and the harmonic confinement becomes an inverted quadratic potential, leading to unstable diverging trajectories. However, the noise in z1 is still substantially increasing in time, and can, in general, complicate both predictions and applications of nonlinearities. For large initial noise, as visible in Fig. 2a (grey), the higher-order nonlinear terms of the Coulomb interaction make for a positive back-action z2 on z1. It results in a decrease of the noise of z1, even below that of its initial thermal state.

When the reciprocity in the nonlinear effect is further broken by either tuning the mass (at fixed frequency) or frequency (at fixed mass) of particle 1, the fluctuations in z1 are modified and the properties of the coherent motion are altered. The initial thermal state of z1 is determined by its dynamical variables m1, ω1, and local environmental temperature T1 via the standard deviation \({\sigma }_{{z}_{1},0}=\sqrt{{k}_{B}T/{m}_{1}{\omega }_{1}}\). Changing the mass or frequency to pursue the symmetry-breaking techniques results in a modification of the initial fluctuations. We therefore fix the noise properties to \({\sigma }_{{z}_{1},0}=30\) nm to observe the effect arising from the nonlinear interaction with constant initial noise across different parameter regimes. That is, z1 is not prepared in an equilibrium state of its local oscillator but rather in an out-of-equilibrium thermally squeezed state.

Trapping a massive particle m1 ≫ m2 minimises its kinetic term \({p}_{{z}_{1}}^{2}/2{m}_{1}\), and as a result, the position does not move away from its initial mean condition \(\left\langle {z}_{1}\right\rangle \approx \left\langle {z}_{1,0}\right\rangle\). That is, the back-action is negligible for short transients, as is visible. Differently than parametric symmetry, the additional imbalance of the mass reshapes the noise evolution of z1, keeping it close to its initial distribution \({\sigma }_{{z}_{1,0}}\) for low initial fluctuations. However, as visible in Fig. 2a (orange), large initial noise promotes a positive back-action loop over time, decreasing the fluctuations of z1 below the initial thermal state. It is similar to the parametric symmetry (grey) back-action effect, however, its effect on particle 2 showcases a larger displacement, although with larger fluctuations (orange shaded area). The resulting SNR in Fig. 1b(i), while increasing even at low fluctuations (empty circles), only saturates the bound for larger initial noise \({\sigma }_{{z}_{1,0}}\) (full circles). The short transient of p2 evolves as \({p}_{{z}_{2}}({t}^{{\prime} })\approx {p}_{{z}_{2},0}+3\kappa \int_{0}^{{t}^{{\prime} }}ds{\prime} \,{z}_{1}^{2}(s{\prime})/{d}^{4}-{m}_{2}{\omega }_{2}^{2}{z}_{2,0}{t}^{{\prime} }\) in the limit of zero damping Γ = 0. For mass tuning, it leads to the following moments

Alternatively, trapping particle 1 in a stiffer harmonic potential ω1 ≫ ω2 confines its noise dynamics to that of a harmonic oscillator for short transients. Its evolution is described by coherent oscillations, approximately described by \({z}_{1}\approx {z}_{1,0}\cos ({\omega }_{1}t)\) under the assumption of vanishing initial velocity \({\dot{z}}_{1,0}=0\). As visible in Fig. 2a (blue), this oscillatory evolution dominates over the back-action for times of a few tenths of microseconds. This added imbalance of frequency negatively impacts the dynamics, generating a lower momentum drift \(\langle {p}_{{z}_{2}}\rangle\), and a lower SNR output Fig. 1b(i) (blue) at small initial noise (empty circles), but it too saturates the \(1/\sqrt{2}\) bound at large initial noise \({\sigma }_{{z}_{1,0}}\) (full circles). For tuning frequencies, the moments of momentum p2 approach

where θ = ω1t.

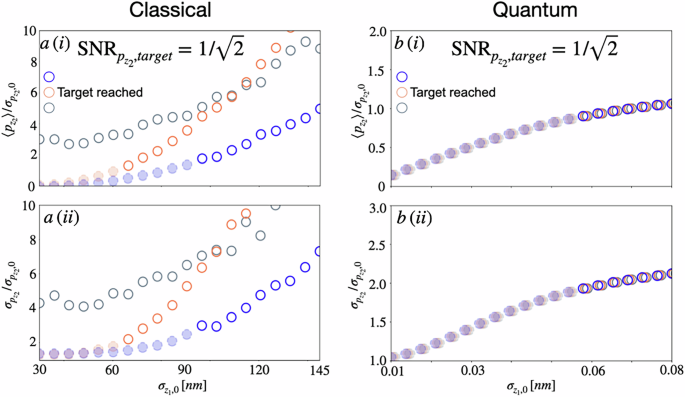
In the low noise limit, the added symmetry breaking lowers the SNR relative to the symmetric case (see Fig. 1b(i), empty circle). To reach it, an extra cost of increasing the initial noise \({\sigma }_{{z}_{1},0}\) is required. Specifically, for tuning stiffness, the same SNR is reached at a smaller displacement (see Fig. 2a, blue), while for tuning mass, the SNR saturation is obtained with a much larger displacement (orange), making it a favourable strategy. This is further highlighted in Fig. 3a, where a target \({{{\rm{SNR}}}}=1/\sqrt{2}\) is fixed, and the output momentum displacement \(\langle {p}_{{z}_{2}}\rangle\) (top) and standard deviation \({\sigma }_{{p}_{{z}_{2}}}\) (bottom) are plotted against input noise cost \({\sigma }_{{z}_{1},0}\). It shows that for initial noise below \({\sigma }_{{z}_{1},0} \, \lesssim \,100\) nm, the parametric symmetry (grey) harnesses the noise of z1 through the Coulomb interaction more efficiently. However, for initial noise input beyond \({\sigma }_{{z}_{1},0} \, \gtrsim \, 100\) nm, tuning frequency (blue) generates the same SNR with smaller output noise and momentum drift, while tuning mass (orange) reaches it with larger momentum drift. Fig. 3 shows that the best strategy, for large initial noise, is to break the symmetry by tuning the mass to reach the target signal-to-noise with the largest momentum drift.

Fig. 3: Noise/Uncertainty-induced momentum under noise confinement.

a The output displacement \(\langle {p}_{{z}_{2}}\rangle\) (i), and standard deviation \({\sigma }_{{p}_{{z}_{2}}}\) (ii) at the target signal-to-noise ratio \({{{{\rm{SNR}}}}}_{{p}_{{z}_{2}}}=1/\sqrt{2}\) are plotted for the stochastic classical dynamics against the input noise \({\sigma }_{{z}_{1},0}\). At low initial input noise, the parametric symmetry (grey) always reaches the target. At large input noise, all regimes reach the target, but breaking the symmetry via tuning frequency (blue) provides the least noise output, and thus even smaller momentum displacement. Breaking symmetry by tuning mass (orange) is useful only between noise input \(60 \, \lesssim \, {\sigma }_{{z}_{1},0} \, \lesssim \, 100\) nm. b The output displacement \(\langle {p}_{{z}_{2}}\rangle\) (i), and standard deviation \({\sigma }_{{p}_{{z}_{2}}}\) (ii) at the target SNR for different initial uncertainty \({\sigma }_{{z}_{1},0}\). All regimes reach the target, but at different times. For parametric symmetry (grey) and tuning frequency (blue), the target is reached at t ≈ 1 μs, while for tuning mass (orange), the target is reached at larger times t ≈ 2 μs. Regardless of the required time, when the target is reached, all regimes produce the same displacement and standard deviation output, making the parametric symmetry (grey) the preferred strategy to reach the target with the minimum noise cost. Note, breaking symmetry requires extra squeezing to reach the same initial noise input. The dashed filled circles record the value of momentum displacement and standard deviation when the target SNR is not reached.

Quantum uncertainty-induced momentum

As we decrease the initial noise to the ground state extension, that is \({\sigma }_{{z}_{1,0}}=0.01\) nm, the nonlinear effect in the stochastic framework described by Eq. (3) vanishes (see SM Note 2). Operating in the quantum regime of Eq. (3), using pure initial states, an analogue of the previous noise-induced phenomena comes directly from the quantum fluctuations in z1. As expected, it is sufficient to produce momentum displacement on z2, as visible in Fig. 2b.

In this section, the numerical simulations are performed directly on Eq. (3), see SM Note 2, using the same parameters outlined in the previous section. All quantities are rescaled by the standard deviation of the initial state. For parametric symmetry, the quantum fluctuations of z1 induce a small drift in the momentum, further enhanced by the quantum fluctuation of z2 through the cubic nonlinearity, reaching \(\langle {p}_{{z}_{2}}\rangle \approx 3\kappa ({\sigma }_{{z}_{1,0}}^{2}+{\sigma }_{{z}_{2,0}}^{2})t/{d}^{4}\). The unwanted back-action force is too small to induce instability, therefore, the noise of z1 does not increase larger than its reference state. It drives the momentum \(\langle {p}_{{z}_{2}}\rangle\) with an increasing SNR (Fig. 3 panel b(i), empty circles) that does not reach the maximum of \(1/\sqrt{2}\), as for times t > 2 μs, the cubic nonlinearity dominates both dynamics and the back-action strongly drives z1 to instability. It enhances the noise of p2 beyond the initial ground state, thus resulting in a drop of the SNR. The conservative symmetry-breaking strategies, introduced for the stochastic dynamics, result in a qualitatively similar time evolution (see Fig. 2b, blue and orange).

The initial standard deviation \({\sigma }_{{z}_{1},0}=\sqrt{\hslash /(2{m}_{1}{\omega }_{1})}\) is calculated using the same parameters of the stochastic system. For parametric symmetry, i.e. m1 = 8 × 10−17 kg and ω1 = 50 kHz, the initial standard deviation results in \({\sigma }_{{z}_{1},0}=0.01\) nm. For tuning frequency, i.e. ω1 = 2500 kHz, and tuning mass m1 = 8 × 10−16 kg, the initial standard deviations assume different values. Respectively \({\sigma }_{{z}_{1},0}=0.001\) nm, and \({\sigma }_{{z}_{1},0}=0.003\) nm. To observe only the effects of the nonlinear interaction given by the dynamics, under the same initial noise conditions, the initial state of z1 is squeezed by a factor \(\xi =-\log ({\sigma }_{trg}\sqrt{{m}_{1}{\omega }_{1}/\hslash })/2\) to reach the unified target standard deviation of σtrg = 0.01 nm. That is, the position variance is amplified \({\sigma }_{{z}_{1},0}=\xi \sqrt{\hslash /(2{m}_{1}{\omega }_{1})}\) by ξ, while the momentum variance is attenuated by the inverse amount \({\sigma }_{{p}_{{z}_{1},0}}=\sqrt{\hslash {m}_{1}{\omega }_{1}/2}/\xi\).

When the initial ground state of z1 is further squeezed in momentum, it realises a larger drift reaching a \({{{\rm{SNR}}}}=1/\sqrt{2}\) at short transients (Fig. 1, panel b(ii)). Notice that parametric symmetry (grey) and tuning frequency (blue) are subjected to instability for times larger than t ≈ 1 μs, resulting in a drop of the SNR, while tuning mass (orange) is not yet affected by it.

For tuning mass m1 ≫ m2, the short transient of the moments of p2 approach

For short transients, the ground state momentum noise \({\sigma }_{{p}_{{z}_{2}},0}^{2}\) prevents the SNR from reaching the \(1/\sqrt{2}\) bound. At larger times it becomes negligible, leaving the position noise \({\sigma }_{{z}_{2},0}^{2}\) as the dominant limiting term of the evolution. For fixed m2, ω2, an amplification of position noise \({\sigma }_{{z}_{1},0}^{2}=\xi {\sigma }_{{z}_{1},0}^{2}\) by ξ allows to reach a \({{{\rm{SNR}}}}=1\sqrt{2}\) as visible in Fig. 1b(ii), full orange circle. That is, the initial state is further squeezed in momentum. Squeezing the position noise \({\sigma }_{{z}_{2},0}^{2}\) can, in principle, improve upon the SNR of Eq. (6). However, the complementary amplification of momentum noise \({\sigma }_{{p}_{{z}_{2}},0}^{2}\) increases the back-action to particle 1 at larger times, thus leading to the divergence quicker.

For tuning frequency ω1 ≫ ω2, the noise of z1 is confined in a stiffer harmonic bound, and its dynamics is described as \({z}_{1}\approx {z}_{1,0}\cos (\theta)\), with θ = ω1t. In this regime, the dynamics evolves similarly to that of the parametric symmetry as visible in Fig. 1b(ii), blue and grey circles. Its momenta evolve in short transients according to

For an initial ground state \({\sigma }_{{z}_{1},0}^{2}=\hslash /(2{m}_{1}{\omega }_{1})\), the momentum and position noise of the initial state of particle 2, i.e. \({\sigma }_{{z}_{2},0}^{2},{\sigma }_{{p}_{{z}_{2}},0}^{2}\) hinders the uncertainty-induced effect from reaching the \({{{\rm{SNR}}}}=1/\sqrt{2}\) bound at short transients. For a longer time, the instability from the cubic potential, not accounted for in Eq. (7), dominates the dynamics, resulting in a drop of the SNR. Similar to tuning mass, to reach the signal-to-noise bound for short transients, the amplification of position noise \({\sigma }_{{z}_{1},0}^{2}\) is required, as visible in Fig. 1b(ii), full blue circles. Moreover, squeezing the position noise \({\sigma }_{{z}_{2},0}\) results in faster divergence, similar to the case of the tuning mass.

The hidden cost of parametric symmetry breaking lies in the preparation of the initial state, which requires squeezing of the ground state. That is, to have comparable noise in position of \({\sigma }_{{z}_{1},0}=0.01\) nm after tuning mass and frequency, the ground state must be squeezed, by ξ = 1.15 and ξ = 1.96, respectively. For the large noise case, a further amplification by free-fall is then used to reach the position noise in all regimes of \({\sigma }_{{z}_{1},0}=0.08\) nm. In Fig. 3b, the target \({{{\rm{SNR}}}}=1/\sqrt{2}\) is reached equally by all regimes for initial input noise \({\sigma }_{{z}_{1},0} \, \gtrsim \, 0.06\) nm, but at different times. Ultimately, the parametric symmetry emerges as the best regime, as it does not require any extra costs, i.e. the initial squeezing to \({\sigma }_{{z}_{1},0}=0.01\) nm, as is the case of the mass and frequency tuning regimes.