Quantum features of gravcats | Scientific Reports

In this section, we delve into the gravcat model using quantum resources to explore its properties with and without dephasing effects.

Without dephasing effect

First, we study the behavior of quantum steerability based on our thermal state (6) as a function of temperature T for some fixed values of the gravitational interaction strength (\(\gamma\)) and the energy gap between the ground state and excited state (\(\omega\)). Since \(\varrho _{2,2}=\varrho _{3,3}\), we obtain \(f_{b}=0\) according to Eq (17b). Thus, the steerability of A to B (19) becomes equal to that of B to A (20), known as two-way steering, namely

and

In Fig. 2(a), we plot the quantum steering versus the temperature T in the logarithmic scale with \(\gamma =1\); \(\omega =0.1\) (red curve), \(\gamma =2\); \(\omega =0.2\) (blue curve), \(\gamma =3\); \(\omega =0.3\) (green curve), and \(\gamma = 5\); \(\omega =0.5\) (black curve). The parts of the system are symmetrical, and their ability to influence each other is equivalent, so \(S_{A\rightarrow B}\) and \(S_{B\rightarrow A}\) are equal (\(S_{A\rightarrow B}=S_{B\rightarrow A}\)). We notice that the steerability reaches its maximum value when \(\gamma\) increases compared to \(\omega\). Moreover, steerability decreases when the temperature increases. This can be explained by the thermal fluctuations phenomenon. Note that the threshold temperature also increases with raising \(\gamma\) and \(\omega\). This remark helps elucidate the relation between the required temperature, mass, distance, and energy scales in experiments aiming to measure this effect.

Fig. 3

Quantum steering in two gravcats versus \(\omega\) and \(\gamma\) with (a) \(T=0.01\) and (b) \(T=0.1\).

In Fig. 2(b), the quantum steering is represented as a function of the temperature T in the logarithmic scale at some fixed values of \(\gamma =0.2\); \(\omega =0.8\) (red curve), \(\gamma =0.4\); \(\omega =1\) (blue curve), \(\gamma =0.6\); \(\omega =1.2\) (green curve), and \(\gamma =1\); \(\omega =1.4\) (black curve). One can observe that, when \(\gamma , the quantum steering is weak: \(S_{A\rightarrow B}=S_{B\rightarrow A}\approx 0.06\) (red curve), \(S_{A\rightarrow B}=S_{B\rightarrow A}\approx 0.14\) (blue curve), \(S_{A\rightarrow B}=S_{B\rightarrow A}\approx 0.2\) (green curve) and \(S_{A\rightarrow B}=S_{B\rightarrow A}\approx 0.34\) (black curve). We have \(S_{A\rightarrow B}=S_{B\rightarrow A}\) (i.e. \(\Delta _{12}=0\)), which implies that the parts of the system are symmetrical. In addition, we see that the quantum steering decreases with the increase in the temperature T. These results are consistent with expectations, as they demonstrate that the greater the mass of the state for fixed distances or the energy scale of the model is elevated, the higher the intensity of gravity-mediated steerability. Similar behavior is observed for smaller distances between particles. However, interactions with the environment, such as decoherence and noise, can lead to undesirable effects that limit steerability, even in the presence of increased potential energy and excitement. It is important to consider other factors and specific conditions that could modulate this relationship in particular circumstances.

We plot in Fig. 2(c) the steearbilities \(S_{A\rightarrow B}\), \(S_{B\rightarrow A}\), and the asymmetry \(\Delta _{12}\) versus the temperature T. We note that \(S_{A\rightarrow B}=S_{B\rightarrow A}>0\) (i.e., \(\Delta _{12}=0\)) when \(T\lesssim 0.2\). This witnesses the existence of two-way steering between qubit A and qubit B. Moreover, when \(T> 0.2\), we have \(S_{A\rightarrow B}=S_{B\rightarrow A}=0\). This means no-way steering between two qubits.

Fig. 4

Quantum steering in two gravcats versus \(\gamma\) and T with (a) \(\omega =2\) and (b) \(\omega = 3.\)

Fig. 5

Quantum steering in two gravcats versus \(\omega\) and T with (a) \(\gamma =3\) and (b) \(\gamma =5\).

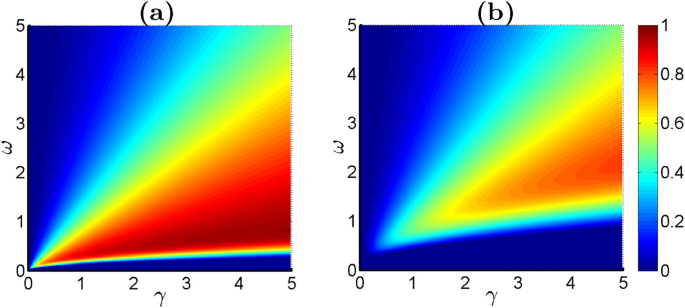
In Fig. 3, we present the steerability as functions of \(\gamma\) and \(\omega\), comparing its properties for two temperatures: \(T=0.01\) in Fig. 3(a) and \(T=0.1\) in Fig. 3(b). For the lower temperature (\(T=0.01\)), we notice that the steerability does not evolve linearly with \(\gamma\) and \(\omega\). For instance, if we fix a specific value of \(\gamma\), we may observe a specific increase/decrease in steerability by changing the value of \(\omega\). However, this trend may vary for other values of \(\gamma\) and \(\omega\), rendering the overall non-monotonic behavior. On the other hand, for a higher temperature (\(T=0.1\)), the steerability initially decreases for relatively low values of \(\gamma\) and \(\omega\). This is due to thermal effects, which introduce more noise and reduce coherence in the system. However, as \(\gamma\) increases, the steerability tends to improve due to stronger correlations among the particles in the system. Similarly, increasing \(\omega\) also enhances the steerability, although its impact is less pronounced than that of \(\gamma\).

Fig. 6

GQD versus (a) \(\gamma\) with \(\omega =1\) and (b) \(\omega\) with \(\gamma =1\) for various values of temperature T.

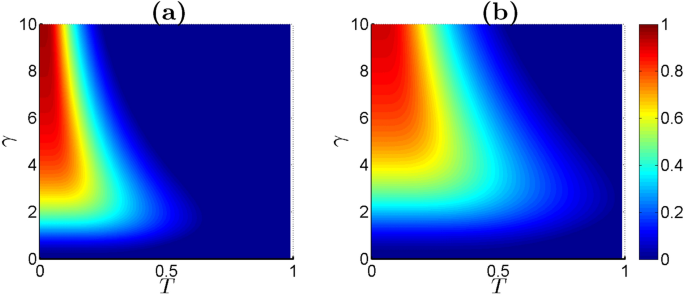
The effects of temperature on steerability are clearly visible in Fig. 4, where we observe steerability as a function of \(\gamma\) and T. As the temperature increases, thermal effects become predominant, leading to an increase in entropy in the system and a decrease in steerability. Comparing Fig. 4(a) and Fig. 4(b), we note that increasing the excitation energy \(\omega\) leads to greater energy availability for quantum processes, thus enhancing steerability under conditions where other variables are constant. Moreover, the gravitational interaction between the two gravcats \(\gamma\) introduces a unique element, that is, the strong gravitational interactions can either amplify or dampen quantum effects, resulting in steerability demonstrating nonlinear behavior.

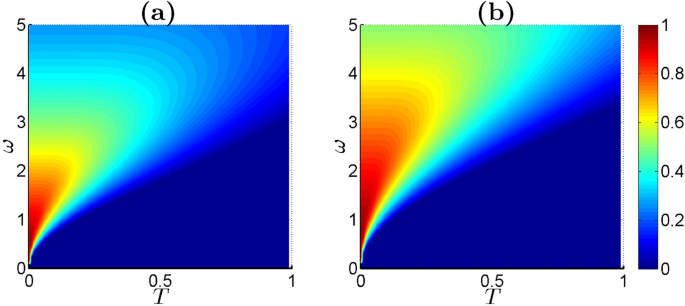
The previously described characteristics of steerability can be confirmed by analyzing Fig. 5, as the system temperature increases, thermal fluctuations become more significant. This generally leads to increased thermal noise, which reduces the quality of quantum information processing and thus decreases the system’s steerability. This phenomenon is evident in Figs. 5(a) and 5(b). Regarding the excitation energy \(\omega\), one observes a nonlinear behavior in steerability. At higher energy levels, there is more energy available for quantum processes, which can enhance the system’s steerability for manipulating and processing quantum information. However, at extremely high values of \(\omega\), other factors such as increased thermal effects may counteract this trend. By comparing Fig. 5(a) and Fig. 5(b), we find a relationship between gravitational effects and steerability. This suggests that the strength of gravitational interactions \(\gamma\) can influence how the quantum system can be used for quantum communication, which could have significant implications for the design and optimization of quantum systems in environments where gravitational effects are significant.

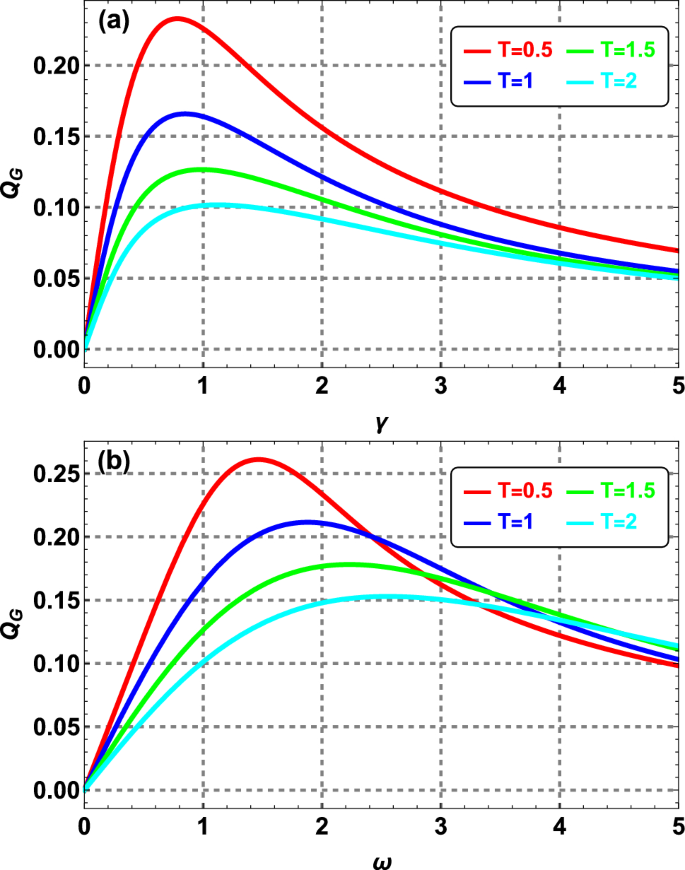
In Fig. 6, we plot GQD as a function of gravitational interaction strength \(\gamma\) [Fig. 6(a)] and excitation energy \(\omega\) [Fig. 6(b)] for various values of temperature T. One observes that as we increase the parameters \(\gamma\) or \(\omega\), GQD rapidly increases to reach its maximum and then decreases to reach a steady-state value. It is also noteworthy that the maximum value of GQD occurs at low temperature and lower values of \(\gamma\) and \(\omega\). However, as depicted in Fig. 6(b), this trend is changed at higher excitation energies. Notably, this suggests a complex relationship between temperature, strength of gravitational interactions, excitation energy, and the measurement of GQD.

Fig. 7

GQD versus temperature T for different values of (a) \(\omega\) with \(\gamma =1\) and (b) \(\gamma\) with \(\omega =1\).

Fig. 8

Quantum steering \(S_{A\rightarrow B}\), concurrence C and GQD \(Q_{G}\:(\)a\()\) as a function of temperature with \(\gamma =2\) and \(\omega =1\), (b) as a function of \(\gamma\) with \(T=0.1\) and \(\omega =1\), (c) as a function of \(\omega\) with \(T=0.1\) and \(\gamma =1\).

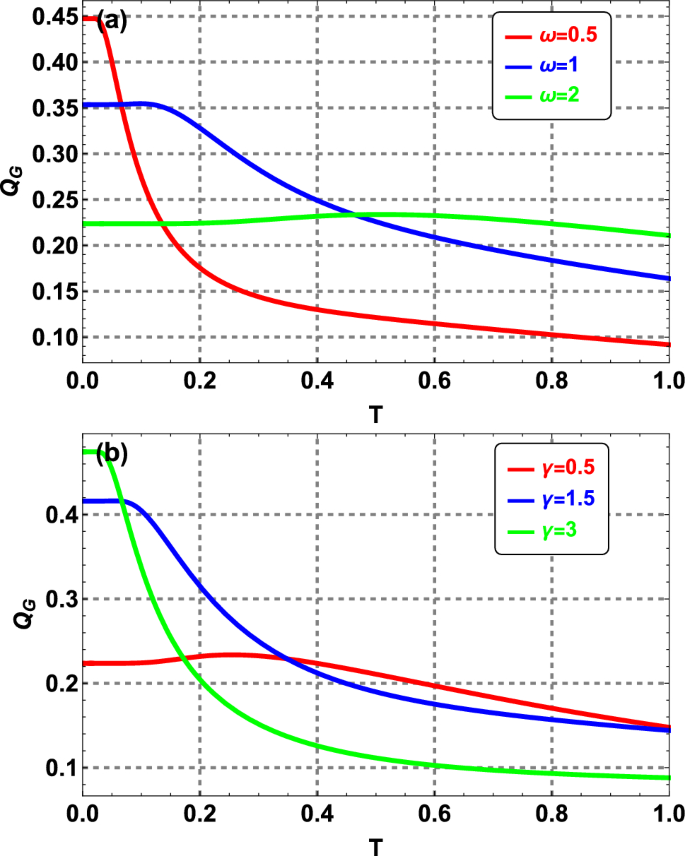
Figure 7(a) depicts the GQD as a function of temperature T for three values of the potential energy. Meanwhile, Fig. 7(b) illustrates the GQD as a function of T for three values of \(\gamma\). As the temperature increases, the GQD decreases after reaching a certain threshold, which is \(T\approx 0.02\) for specific values of \(\omega =0.5\) and \(\gamma =1\), as depicted in Fig. 7(a). However, for a different value of \(\omega\), for example, \(\omega =2\), the GQD decreases more smoothly and steadily around 0.2. At lower temperatures, decreasing \(\omega\) (or \(\gamma\)) can lead to an increase (or decrease) in GQD. However, this relationship can no longer hold at higher temperatures.

Fig. 9

Time (t) dependence of quantum steering (a), concurrence (b), and GQD (c) in the Markovian regime for different values of \(\mu\) with \(4\omega = \gamma =2\), \(T=0.01\) and \(\tau =0.1\).

Fig. 10

Time (t) dependence of quantum steering (a), concurrence (b), and GQD (c) in the non-Markovian regime for different values of \(\mu\) with \(4\omega = \gamma =2\), \(T=0.01\), and \(\tau =5\).

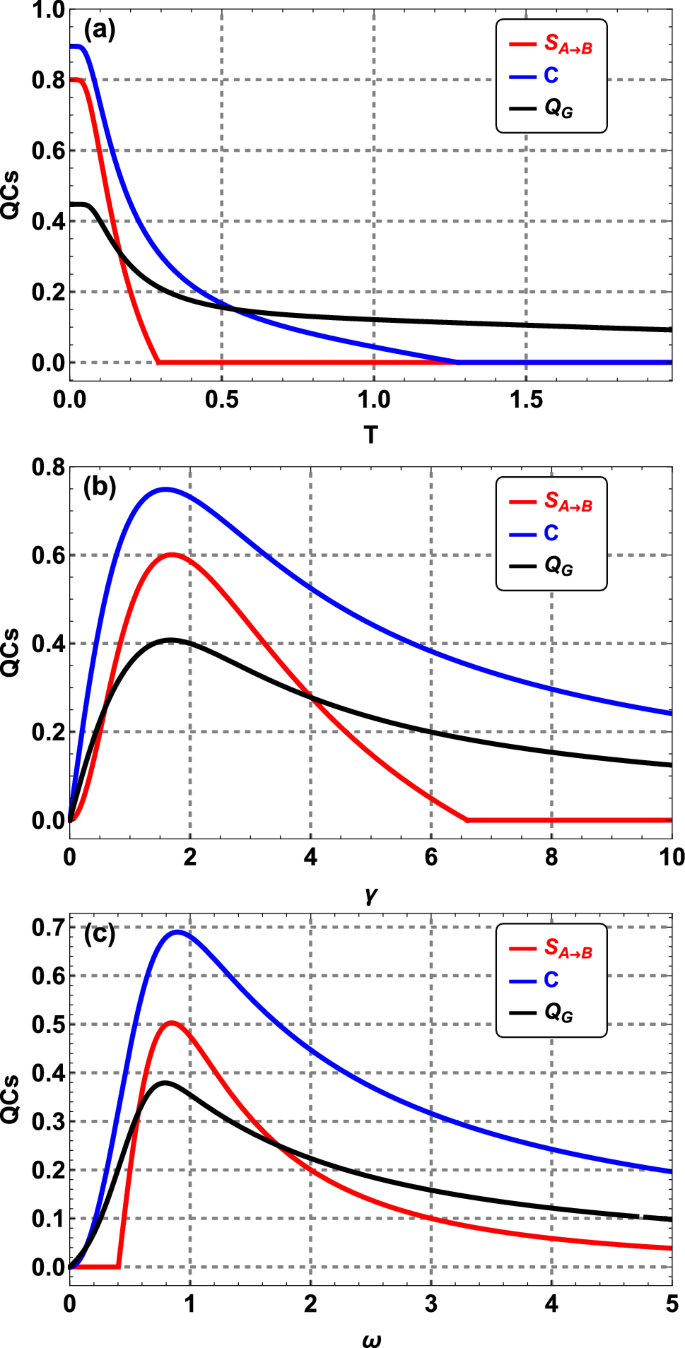
In Fig. 8(a), we investigate quantum steering, concurrence, and GQD as a function of temperature. This figure illustrates the hierarchy of quantum correlations, revealing how they evolve with temperature. When \(0.28 \lesssim T \lesssim 1.2\), GQD and concurrence remain significant, while the steering \(S_{A\rightarrow B}\) is zero. This suggests that the two gravcats are entangled (\(C>0\)) in this range of temperature. Furthermore, it can be observed that the gravcat state can be entangled even when it is not necessarily steered. It is also noted that the steering \(S_{A\rightarrow B}\) is bounded by the concurrence C. Additionally, when \(T>1.2\), quantum correlations beyond entanglement manifest between the two gravcats, as GQD persists despite the absence of concurrence. Interestingly, these results are in good agreement with the hierarchy of quantum correlations where quantum steering \(\subseteq\) entanglement \(\subseteq\) quantum discord82,83.

We plot quantum steering, concurrence, and GQD versus gravitational interaction strength \(\gamma\) [Fig. 8(b)] and excitation energy \(\omega\) [Fig. 8(c)]. We observe that quantum steering \(S_{A\rightarrow B}\), concurrence C, and GQD \(Q_{G}\) exhibit similar behaviors. When \(\gamma >6.6\) (or \(\omega ) in Fig. 8(b) (or in Fig. 8(c)), quantum steering is zero, while concurrence has a nonzero value. This implies that a steerable state must be entangled, even though not all entangled states are necessarily steerable, as illustrated in Fig. 8 and Ref.82. Notice, within the region where entanglement is absent, the GQD of the system is still considerably greater than zero [see Fig. 8(a)], ensuring the presence of correlated quantum states even when the system is in a separable state.

Fig. 11

Comparison of the time (t) dependence of quantum steering, concurrence, and GQD in (a) Markovian regime with \(\tau =0.1\) and in (b) non-Markovian regime with \(\tau =5\). Fixed values are: \(\gamma =2\), \(\omega =0.2\), \(\mu =0\), and \(T=0.01\).

Under dephasing effect

When gravcat states interact with their environment, they experience decoherence, particularly through dephasing channels that affect their phase information. In this context, gravcat states under a correlated dephasing channel would experience a collective phase noise that depends on the positions or states of the objects, leading to the potential preservation of quantum resources for longer times compared to uncorrelated noise. Here, we investigate how gravitational superpositions decay due to environmental factors, with the presence of correlated noise potentially offering insight into ways to protect quantum resources against decoherence.

According to our thermal time-dependent state (12), the analytical expressions for quantum steering, concurrence and GQD would be simply obtained by replacing \(\varrho _{2,3}\) and \(\varrho _{1,4}\) with \(\eta \varrho _{2,3}\) and \(\eta \varrho _{1,4}\), respectively, in Eqs. (19)-(20), (24), and (28), where \(\eta =\Phi ^{2}(t)+\left[ 1-\Phi ^{2}(t)\right] \mu\).

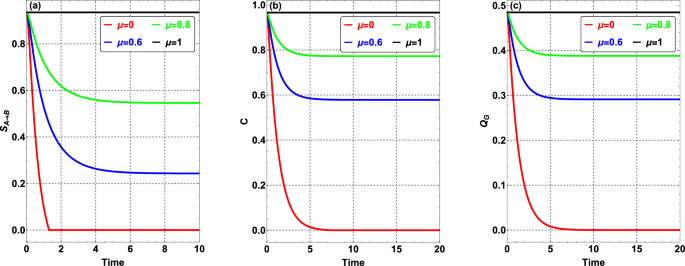
Figure 9 shows the effect of classical correlations (measured by \(\mu\)) on the time evolution of quantum resources in a Markovian environment. The results indicate that quantum steering, concurrence, and GQD can be significantly enhanced by increasing classical correlations. For \(\mu , all quantities decrease exponentially over time. Moreover, for \(\mu =0\) (\(\eta =\Phi ^{2}(t)\)), steering, concurrence, and GQD decrease more rapidly and tend towards zero with time, indicating the negative effect of reduced classical correlations on protecting quantum resources. When \(\mu =1\) (a fully correlated dephasing channel), all quantities remain stable over time because \(\eta\) becomes one in Eq. (12) and so, we have \(\varrho _{T}(t)=\varrho _{T}\) in this particular case.

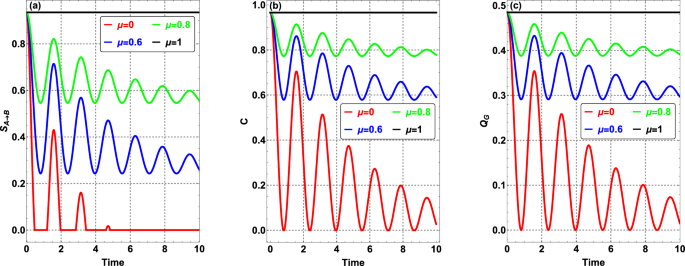
In Fig. 10, our analysis extends to the non-Markovian regime. We observe that when \(\mu =1\), all measures remain constant, demonstrating stability over time. In the absence of classical correlation (\(\mu =0\)), the curves eventually converge to equilibrium values identical to those in the Markovian regime. For low values of \(\mu\), oscillatory behavior is observed over time in all quantities due to memory effects, with the amplitude of oscillations gradually decreasing.

These results highlight the importance of classical correlations in maintaining quantum resources. High values of \(\mu\) (e.g. \(\mu \rightarrow 1\)) in both Markovian and non-Markovian regimes ensure increased stability and longevity of quantum resources. Conversely, the reduction of classical correlations causes a rapid decay and loss of non-classical correlations. Moreover, the oscillatory behavior observed in the non-Markovian regime reveals a complex relation between classical correlations and memory effects in the evolution of quantum resources over time.

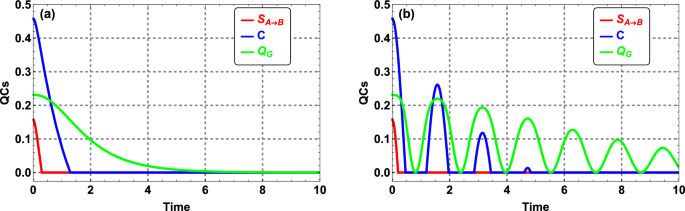
For a detailed comparison between the quantum sources studied in this work, we plot in Fig. 11 the steerability, concurrence and GQD as a function of time in the Markovian regime [Fig. 11(a)] and non-Markovian regime [Fig. 11(b)]. In Fig. 11(a), one can see that the hierarchy of quantum correlations holds here, namely quantum discord \(\supseteq\) entanglement \(\supseteq\) quantum steering. This implies that the two gravcats remain entangled, even if the steered state (steerability) is zero. It is observed that the gravcat state can be entangled even when it is not necessarily steered. One can observe the same description in Fig. 11(b), except that these correlations evolve sinusoidally and in phase.