Making quantum collision models exact

We consider, in the Schrödinger picture, a general Hamiltonian where a non-specified system interacts linearly with a bosonic environment

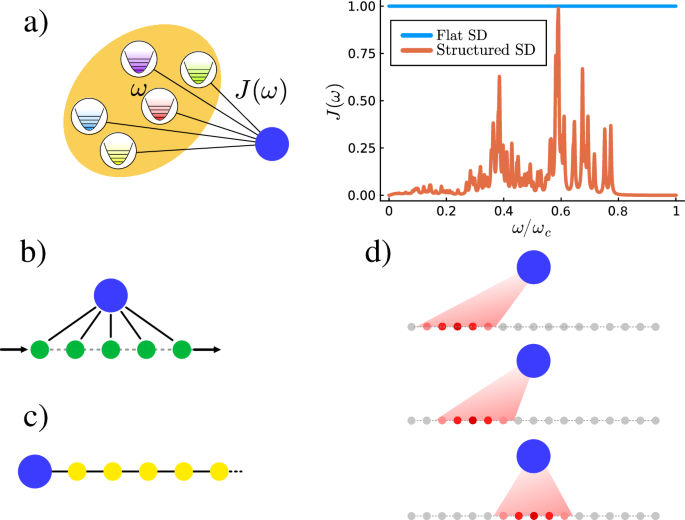
where \({\hat{a}}_{\omega }\,({\hat{a}}_{\omega }^{{{\dagger}} })\) is a bosonic annihilation (creation) operator for a normal mode of the environment with angular frequency ω, \({\hat{A}}_{S}\) is a system operator, and J(ω) is the bath spectral density (SD) and encodes the coupling strength between the system and the bath modes. There exist several definition of non-Markovianity26,27,28,29. In this work, we adopt the perspective commonly used in quantum optics, where any spectral density (SD) that is not flat is considered indicative of a non-Markovian environment30.

We first introduce the frameworks of collision models (CMs) and chain mapping respectively.

Collision models

The fundamental concept behind quantum collision models is the characterization of the interaction between a quantum system S and its environment (or bath) E as arising from repeated interactions with auxiliary systems, referred to as probes (or ancillae), which collectively represent the environment and share the same initial state η. The system evolves through a sequence of pairwise interactions with each probe, which we call collisions. A Markovian CM is defined by the following properties:

C1 the probes are uncorrelated, e.g. the initial state of the bath is (η ⊗ η ⊗ . . . );

C2 probes do not interact with each other;

C3 each probe is discarded after the interaction with the system and is replaced with a fresh one before the next collision.

Additionally, we require that system and environment are uncorrelated at the initial time:

where subscript 0 indicates the initial time, σ the joint system-environment state and ρ0 is the initial state of S. The conditions C1–C3 are fully consistent with the second-order perturbation theory derivation of the Markovian master equation for a discrete dynamics. Within these assumptions the dynamics of S is decomposable into a sequence of elementary completely-positive maps and thus its temporal evolution can be effectively described through a Master Equation in Lindblad form in the continuous-time limit13,19. When one or more of the aforementioned assumptions is violated, this is no longer possible. This is often interpreted as the introduction of memory effects into the time evolution of the system. In a general context, describing the dynamics of an open system through collisions necessitates the proper treatment of the Hamiltonian governing the interaction between the system and its surrounding environment. This involves deriving the discretized system-environment coupling Hamiltonian from a microscopic model that accounts for the interactions between the system and the bath. Starting from the general model in (1) we can move to the interaction picture with respect to the bath Hamiltonian

where we have scaled the SD with a coupling strength \(g\in {\mathbb{R}}\) for later convenience, and define the time-domain ladder operators

It’s important to highlight that in what follows we will deliberately avoid moving to the interaction picture with respect to the system’s Hamiltonian and refrain from introducing the rotating wave approximation (RWA). While we acknowledge that these two approximations play a critical role in establishing a self-consistent definition of Markovian collision models17, we have chosen to maintain a more general model for the purpose of comprehensive comparison with chain mapping.

In terms of the time-domain operators, the final discrete-time generator of the joint system-bath dynamics obtained from discretizing the Hamiltonian in the time-domain in units of Δt, which for now is only assumed small with respect to the inverse of the characteristic frequencies of the system-bath interaction, reads (see Supplementary Note 1 for details)

where \(n\in {\mathbb{N}}\) is a discrete time index such that tn = nΔt, and with the Fourier transform of the spectral density defined as

If we now replace the Fourier transform of the SD with its average over Δt we find

with

The Equations (7), (8) and (9) collectively define the effective quantum collision model describing our dynamics: the system interacts with a set of time-bin modes defined by the ladder operators \(({\hat{a}}_{m},{\hat{a}}_{m}^{{{\dagger}} })\), which act as the ancillae. Note that, according to (7), the system couples nonlocally to all the ancillae with coupling rate Wnm. Figure 1 (b) shows a schematic drawing of collision models. We retrieve the condition C3 if, after performing the RWA17 in the interaction picture with respect to the system’s Hamiltonian, we put \({{{\mathcal{F}}}}[\sqrt{J}](s-{t}^{{\prime} })=\delta (s-{t}^{{\prime} })\) that directly implies Wnm = δnm making the system only interacts with a single ancilla at once. Note that in the frequency space this corresponds to a perfectly flat coupling and only in that case the system dynamics can be expressed with a dynamical map for an arbitrary Δt. Conversely, in the other cases we are describing a system interacting with a colored-noise bosonic reservoir18.

Chain mapping

Let us consider the Hamiltonian presented in Eq. (1). We can introduce a unitary transformation of the continuous normal modes \({\hat{a}}_{\omega }\) to an infinite discrete set of interacting modes \({\hat{b}}_{n}\)20

where Pn(ω) are real orthonormal polynomials such that

and the inverse transformation is

Note that the orthonormality of the polynomials ensures the unitarity of the transformation defined in Eq. (10). The mapping from a continuous set of modes to a (still infinite) discrete set might seem counter-intuitive, however it is a direct consequence of the separability of the underlying Hilbert space. Equation (12) can be seen as a change of basis between a generalized continuous basis of the Hilbert space (labeled with ω) and a discrete one (labeled with n). Accordingly, it also corresponds to a generalized Fourier transform using orthogonal polynomials Pn(ω) as basis functions (instead of \({{{{\rm{e}}}}}^{-{{{\rm{i}}}}\omega t}/\sqrt{2\pi }\) for the usual Fourier transform). So far, the physical interpretation of the chain modes remained elusive. Under this transformation, the Hamiltonian in Eq. (1) becomes (see Supplementary Note 2)

Hence, this mapping transforms the normal bath Hamiltonian into a tight-binding Hamiltonian with on-site energies εn and hopping energies tn. Another important consequence of this mapping is that now the system only interacts with the first mode n = 0 of the chain-mapped environment. Figure 1(c) shows a schematic drawing of this new topology. The chain coefficients εn, tn, and the coupling κ depend solely on the SD (see Supplementary Note 2). This makes chain mapping a tool of choice for describing systems coupled to an environment with highly structured SD (e.g. experimentally measured or calculated ab initio)31,32,33,34. In this new representation, the Hamiltonian in Eq. (13) has naturally a 1D chain topology. This makes the representation of the joint {System + Environment} wave-function as a Matrix Product State (MPS) very efficient35,36. The orthogonal polynomial-based chain mapping and the subsequent representation of the joint wave-function as a MPS (and the operators as Matrix Product Operators) are the building blocks of the Time-Evolving Density operator with Orthonormal Polynomials Algorithm (TEDOPA) one of the state-of-the-art numerically exact method to simulate the dynamics of open quantum systems especially in the non-Markovian, non-perturbative regimes both at zero and finite temperatures21,37,38,39,40 (see Supplementary Note 2 for more details). TEDOPA has been applied, for instance, to transport of electronic excitations in the presence of structured vibrational environment37, photonic crystals41, non-equilibrium steady states42, molecular systems32,43,44, vibration-induced coherence31, or the calculation of absorption spectra of chromophores33,45,46 and pigment-protein complexes34,47.

Here we adopt a slightly different starting point and implement the chain mapping introduced in (10) after moving to the interaction picture with respect to the bath Hamiltonian, the Hamiltonian in (3) reads

where the \({\hat{b}}_{n}\) operators are the discrete chain modes defined in (10) and the time-dependent coupling coefficients are

It can also be noted that the coupling coefficient defined by Eq. (15) can be expressed as a Fourier transform

where \({{{\mathcal{F}}}}[\circ ]\) is the Fourier transform of \(\circ\). In this new representation of the system and the environment, the chain modes are now non-interacting and all coupled to the system with time-dependent coupling48. In the interaction picture the chain mapping brings us from a star topology (see Fig. 1a) of the system-environment interactions with constant coupling strengths \(\sqrt{J(\omega )}\) to another star topology where the couplings between the system and the environmental modes are time-dependent γn(t).

Equivalence in the Non-Markovian case

In this section we prove that non-Markovian collision models can be recovered from chain mapping.

Theorem 1

For any positive bath spectral density J(ω), chain mapping is equivalent to a non-Markovian collision model with \(\Delta t=\frac{\pi }{{\omega }_{c}}\), where ωc is the bath cut-off angular frequency.

In the chain mapping approach there is no fundamental difference between the Markovian and non-Markovian case. Here we want to discuss the general case of non-Markovian environment, namely when the SD is frequency-dependent. The following derivation applies to any SD including, for instance, the highly structured ones found in biological contexts34,49. As outlined above, the usual chain mapping is to use the unitary transformation defined by the set of orthonormal polynomials with respect to the measure J(ω) (see Supplementary Note 2). Thus, for different SD the chain operators \({\hat{b}}_{n}\) would be a different linear combination of the normal modes \({\hat{a}}_{\omega }\). In any case, the time-dependent coupling coefficients are given by (16). These coupling coefficients have, a priori, an unknown behavior.

The proof of Thm. 1 relies on noting the following fact. If we perform the chain mapping unitary transformation in (10) with respect to a flat measure regardless of the nature of the actual SD, we can see that the time-dependent couplings γn(t) will be given by the convolution of the Fourier transform of the square-root of the SD (i.e. the frequency-dependent system-environment coupling strength) and the flat measure coupling coefficients \({\gamma }_{n}^{{{{\rm{M}}}}}(t)\)

Lemma 2

For a flat SD, the coupling coefficient \({\gamma }_{n}^{{{{\rm{M}}}}}(t)\) between the system and any chain mode n is non-zero only at a single time tn.

We consider a flat spectral density up to a cut-off frequency ωc

where \({\Pi }_{{\omega }_{c}}(\omega )\) is the indicator function of the interval [0, ωc] where it takes the value 1 while vanishing on the complement. Introducing a frequency cut-off to our environment makes the calculations below more technical, however this is how numerically exact methods such as TEDOPA are implemented in practice. Hence we believe that the results obtained below will prove more fruitful with the introduction of this frequency cut-off. With this choice of SD, the orthonormal polynomials defining the chain modes are shifted Legendre polynomials (see Supplementary Note 2). It can be shown that the cut-off frequency ωc always corresponds to the cut-off frequency of the bath SD J(ω) (see Supplementary Note 3).

Proof

The coupling coefficients are given by

The shifted polynomials can be expressed in terms of the regular Legendre polynomials Pn which are defined on the support [ −1, 1]: \({P}_{n}(x)={P}_{n}^{{{{\rm{shifted}}}}}(\frac{x+1}{2})\), with x = ω/ωc. Hence, we have

We can perform a so called plane-wave expansion of the exponential on the Legendre polynomials50

where Jν(θ) is the Bessel function of the first kind. Inserting this expansion in Eq. (21) and using the polynomials orthogonality, we have

We can find the limit of the time-dependent coupling coefficients \({\gamma }_{n}^{{{{\rm{M}}}}}(t)\) when ωc is large by using the asymptotic expansion of the Bessel function Jν(θ) for large θ51

Taking the limit of infinitely large cut-off frequency (see Supplementary Note 4), we have

Hence, for a flat SD, the coupling coefficient \({\gamma }_{n}^{{{{\rm{M}}}}}(t)\) between a chain mode n and the system is non-zero only for tn = nπ/ωc = nΔt.                            □

Remark

Lemma 2 extends naturally to the exactly Markovian case of a spectral density flat along the whole real line. In that case the spectral density is chosen to be a rectangular function on the interval \([-\frac{{\omega }_{c}}{2},\frac{{\omega }_{c}}{2}]\) to ensure the same bandwidth. The polynomials are thus directly the Legendre polynomials

from which the same derivation follows leading to the same result.

Equipped with Lemma 2 we can now prove Thm. 1

Proof

The time-dependent coupling coefficients are given by

Therefore, the chain-mapped interaction-picture interaction Hamiltonian is

The time integral of the interaction picture Hamiltonian is the generator of the time-ordered time-evolution operator

where \(\Delta t=\frac{\pi }{{\omega }_{c}}\) and

If we consider \({\hat{a}}_{n}{=}^{{{{\rm{def.}}}}}\frac{2\pi }{\sqrt{\Delta t}}{\hat{b}}_{n}\) as an ancilla operator, we recover (7) defining non-Markovian collision models

                                                                                                              □

We note that, as in collision models (see (9) and (8)), the ancillae \({\hat{a}}_{n}\) and collision rates Wnm scale as \({(\sqrt{\Delta t})}^{-1}\). However, there is a fundamental difference between the collision models rates Wnm defined in (8) and those obtained from the chain mapping approach in (31). Indeed, (34) is an exact result: no averaging to decouple a convolution product was performed. The continuous time limit Δt → 0 is widely recognized as a source of challenges in quantum collision models since it demands careful consideration and specialized treatment19. Remarkably, these challenges do not arise in the context of chain mapping, where the limit ωc → ∞ is usually never formally taken. It is thus interesting to see that these two limits become equivalent within the prescription for the time step Δt = π/ωc. We note that this coarse-grained timescale Δt satisfies the Shannon-Nyquist sampling theorem. For non-vanishing Δt the collisional generator in (34) remains valid with collision rates Wnm being obtained thanks to (17) and (23). The sequential interaction between the chain modes and the system is preserved by the convolution in Eq. (17). Yet, depending on the form of \({{{\mathcal{F}}}}\left[\sqrt{J}\right](t)\), several modes can be interacting with the system at a given time, and conversely chain modes interact more than once with the system. This new representation of the system-bath interaction is represented in Fig. 1d. After a certain time, the number M of chain modes a system interacts with can be considered constant. This is an instance of collision model with multiple non-local collisions19 with M ancillae at a time.

Equivalence in the Markovian case

The case of Markovian collision models is a corollary of Thm. 1. It follows naturally from Lemma 2 that shows that, for a flat SD, a chain mode n couples to the system only at single time tn.

Corollary 2.1

If the bath spectral density is flat with a frequency cut-off ωc larger than the energy scale of the system (i.e. a Markovian environment), then chain mapping is equivalent to a collision model with \(\Delta t=\frac{\pi }{{\omega }_{c}}\).

Proof

The time-evolution operator in the interaction picture is

where \(\overleftarrow{T}\) is the time-ordering operation. Given lemma 2 and Eq. (35), we have

where we introduced the coarse-grained timescale \(\Delta t=\frac{\pi }{{\omega }_{c}}\), N = t/Δt, \({\gamma }_{n}=\int_{0}^{t}{\gamma }_{n}(\tau ){{{\rm{d}}}}\tau ={(2\pi )}^{\frac{3}{2}}g\). All the terms in the sum commute with one another, and we can also assume without loss of generality that they commute with \({\hat{H}}_{S}\), thus we have \([{\hat{H}}_{n}^{I},{\hat{H}}_{m}^{I}]=0\). This is the same situation as in the derivation of collision models, either \(\left[{\hat{H}}_{S},{\hat{A}}_{S}\right]=0\), or we move to the interaction picture with respect to the system and bath free Hamiltonians. In the ‘worse’ case scenario the evolution operator can be Trotterized. We can write the time evolution operator as

with \({\hat{{{{\mathcal{U}}}}}}_{K}={{{{\rm{e}}}}}^{-\frac{{{{\rm{i}}}}}{\hslash }{\hat{H}}_{K}^{I}\Delta t}\). Hence, we have made explicit that, in the Markovian limit, the time-evolution takes the form of a succession of interactions between the system and individual non-interacting environmental modes, with time-steps Δt.                                                                                □

This shows that we recovered a Markovian collision model for bosonic environments starting from the chain mapping of a microscopic Hamiltonian. Furthermore, the collisional dynamical map is recovered by tracing out the ancillae degrees of freedom from the time-evolution operator \({\Lambda }_{\Delta t}={{{{\rm{tr}}}}}_{E}[{\hat{{{{\mathcal{U}}}}}}_{K}\eta ]\) (where \({{{{\rm{tr}}}}}_{E}\) is the partial trace on the ancillae). Here again, the connection with collision model can be made even more explicit if we recast the interaction part of the argument of the time evolution operator as follows

where \({\hat{a}}_{n}{=}^{{{{\rm{def.}}}}}\frac{2\pi }{\sqrt{\Delta t}}{\hat{b}}_{n}\) would play the role of the ancilla operator, and the characteristic factor of \({(\sqrt{\Delta t})}^{-1}\) of the collision model coupling strength is recovered19.

If we compare (39) with (14) we can observe that collision models and chain mapping are two different ways to take into account the same time-dependent behavior of the Hamiltonian, which arises when moving to the interaction picture. In collision models the interaction Hamiltonian is fixed in time and the time dependence is represented by the sequential interaction with the time modes whereas in the chain-mapping picture the time dependence is entirely attributed to the coupling γn(t).

Sources of Error in Collision Models

From their canonical derivation collision models rely on an expansion of the time-evolution operator to second-order in Δt which thus leads to a so called ‘truncation error’ of the reduced system’s dynamics of order \({{{\mathcal{O}}}}(\Delta {t}^{3})\)19,52. In numerical simulations the time-evolution operator is usually approximated using a Trotter-Suzuki decomposition53, inducing a ‘Trotter error’ that can be matched with the usual truncation error \({{{\mathcal{O}}}}(\Delta {t}^{3})\) by using a second order Troterization. The error originating from the truncation of the infinite-dimensional local Hilbert spaces of the bath modes vanishes with the increase of the aforementioned local dimensions21. When combined with tensor networks, another common numerical error is the Singular Value Decomposition truncation error. Properly choosing the threshold for discarding singular values enables to keep this error lower than the previous ones.

However, for non-Markovian collision models, there is an additional source of error to take into account that also stems from the very derivation of the method: the bath correlation function sampling error. This sampling process can be naturally understood by interpreting system-environment interactions as a continuous-time measurement process3,54,55,56. Therefore, replacing this continuous acquisition by a discrete one amounts to a sampling procedure which can be accompanied by a sampling error. In return an unfaithful sampling of the bath correlation function will lead to an error on the system dynamics as the system dynamics is entirely determined (for Gaussian environments) by the bath correlation function. This sampling error is introduced in (7), (8) and (9) when discretizing the time-domain Hamiltonian and averaging the Fourier transform of the square-root of the SD to get rid of the convolution product. The order of the sampling error of the bath correlation function is a priori unknown and needs to be quantified in order to be compared to the other sources of error. Given that the SD is non-negative, sampling \(\sqrt{J(\omega )}\) gives the same information as sampling J(ω). The Shannon-Nyquist sampling theorem tells us that when we sample with a frequency 1/Δt, we can reconstruct the SD up to ω = π/Δt using so called ‘perfect reconstruction’ with, for instance, Whittaker’s interpolation57,58,59. Hence when Δt ≤ π/ωc the SD is perfectly sampled, and when Δt > π/ωc a sampling error is introduced. For Markovian collision model this sampling error does not exist as any time-step Δt yields to the exact SD. That is why a single ancilla is sufficient to describe the dynamics. However, for non-flat SD this sampling error can become larger than the truncation (or Trotter) error for Δt > π/ωc even though the time step can be made arbitrary small numerically.For the Spin Boson Model (SBM), the impact of this sampling error on the expectation value of an observable can be upper bounded22. The sampling error on the expectation value 〈σz〉(t) after a single time step Δt is

Let us consider an Ohmic SD \(J(\omega )=2\alpha \omega {\Pi }_{{\omega }_{c}}(\omega )\),

is the difference between the exact bath correlation function and the sampled one. The sampling error vanishes for Δt ≤ π/ωc because the upper and lower integration bounds in (41) are equal. For \(\Delta t\ge \frac{\pi }{{\omega }_{c}}\) the error is

Thus, for a SBM with an Ohmic SD, when Δt ≤ π/ωc the leading error is the truncation/Trotter error \({{{\mathcal{O}}}}(\Delta {t}^{3})\), and when Δt > π/ωc the leading error is the sampling error \({{{\mathcal{O}}}}(\Delta {t}^{2})\).

Spin Boson Model

The SBM is a paradigmatic model in the field of OQS. While being simple—the model consists of a single spin linearly coupled to a bosonic bath—its physics is rich (and exhibits non-Markovian behavior) and it has been used to model magnetic impurities, charge transfer, chemical reactions, strangeness oscillations of the K0 mesons, or decoherence55,60. On top of its dynamics being non-trivial, the model is also non-solvable analytically and has become a test-bed for numerical methods describing open systems. From Eq. (1) the SBM Hamiltonian is obtained by setting

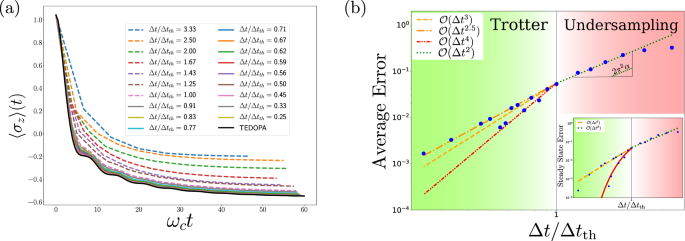
We note that in this model no rotating wave approximation has been performed. In the following we consider an Ohmic SD with a hard cut-off \(J(\omega )=2\alpha \omega {\Pi }_{{\omega }_{c}}(\omega )\) with \({\Pi }_{{\omega }_{c}}(\omega )\) the rectangular function on [0, ωc]. Figure 2a shows the expectation value of 〈σz〉(t) obtained with a non-Markovian collision model for several values of Δt, compared with the dynamics obtained with the regular Schrödinger picture chain mapping (i.e. the TEDOPA method) taken as a reference result. The TEDOPA results are obtained considering 16 environmental modes, and the maximum bond dimension reached during the simulation is D = 15. The non-Markovian collision model has been implemented with tensor networks methods: The {System + Ancillae} density matrix is represented as a purified Matrix Product State61,62 and the time-evolution is performed with the standard time-evolving block decimation (TEBD) method36,63. The results are obtained with a number of ancillae inversely proportional to Δt (e.g. 35 for Δt = 1/ωc, 70 for Δt = 2/ωc, and 280 for Δt = 1/2ωc), and a maximal bond dimension of D = 32. We would like to point out that, to the best of our knowledge, this is the first time that the SBM has been simulated with a collision model. It has to be noted that, because the cut-off frequency ωc of the SD remains ‘small’ in numerical simulations, the threshold time-step in these simulations is Δtth = 2/ωc instead of π/ωc (see Supplementary Note 5). This is due to the asymptotic behavior of spherical Bessel functions. On Fig. 2a we can see that both the steady state and the transient dynamics are better described when Δt diminishes. For instance, the oscillatory dynamics start to be well caught around Δt = 2/ωc. The dynamics converges monotonically from above with decreasing time steps. Figure 2b (main panel) shows the average error during the dynamics of the collision model simulations with respect to the reference one. We can clearly see that there are two different scaling regime separated by the threshold value Δtth. For time step smaller than the threshold Δt tth we are in a regime where the deviation is dominated by an error \({{{\mathcal{O}}}}(\Delta {t}^{2.5})\) associated with the second order Trotterization performed to obtain the collision model time-evolution operator. We also note that for specific values of Δt in this regime the error can be smaller than the Trotter error—which is perfectly legitimate considering that the Trotter scaling is an upper bound. This might originate from ‘local’ error cancellation. The investigation of this ‘super-performance’ is beyond the scope of this paper. When the time step is larger than the threshold Δt > Δtth we can see a sudden change in the scaling of the error that is now \({{{\mathcal{O}}}}(\Delta {t}^{2})\) (for large Δt the error saturates because 〈σz〉(t) decays exponentially to 0). We attribute this additional source of error to a fundamental inaccuracy of the collision model in this regime, as can be inferred from the equivalence theorem. When Δt > Δtth the scaling of the errors in our simulations have a slope of 2π2α in agreement with the one expected from the discussion in the subsection “Sources of Error in Collision Models”, and thus shows that in the fundamental inaccuracy regime an aliased sampling of the bath correlation function results in an error of order \({{{\mathcal{O}}}}(\Delta {t}^{2})\). The distance between the steady state expectation value 〈σz〉(t → ∞) and the reference one for different values of the time step Δt is presented in the inset of Fig. 2b. Here again we find the same transition between two scaling regimes of the error at Δtth. For time steps larger than the threshold Δt > Δtth we have a scaling of \({{{\mathcal{O}}}}(\Delta {t}^{2})\) worse than the Trotter one \({{{\mathcal{O}}}}(\Delta {t}^{3})\) which is recovered for time steps smaller than the threshold value Δt tth. These results show that, in order to give physically accurate results, the chosen time step of the collision model has to be lower or equal to the threshold value Δtth. This prescription gives a consistent definition to how small the time step needs to be to ensure the validity of collision models.