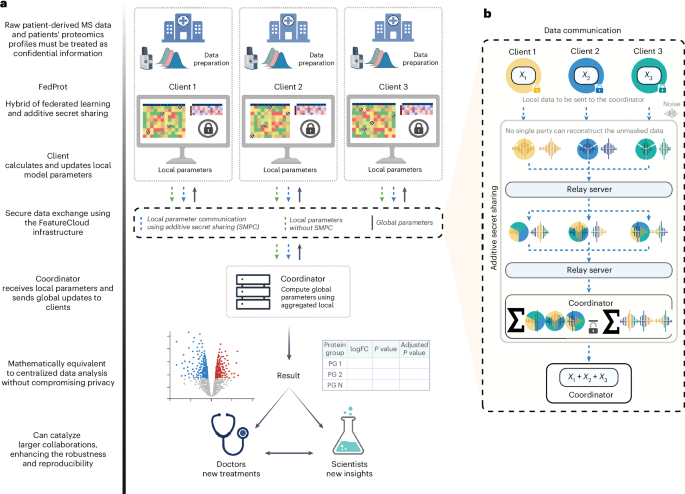
FedProt is based on the accurate variance estimation workflow of DEqMS33 for MS data and uses the hybrid approach of federated learning and additive secret sharing30 in a manner similar to Flimma27. Federated learning is a machine learning paradigm in which models are trained on multiple devices (clients) without centralizing data, enabling collaborative learning with increased data privacy. Clients securely store and analyze their local data and exchange intermediate results with the trusted server (Coordinator) that aggregates local results to global.
Before the federated analysis, each participant preprocesses its local dataset independently and is responsible for ensuring the quality and consistency of the data provided to the client app. We assume that all the participants used the same protocol to quantify and preprocess their local data.
The FedProt’s federated analysis workflow is divided into six (or seven if normalization is needed) steps, of which four (or five) involve federated computations and require one or several rounds of communication between client and server (Fig. 3).
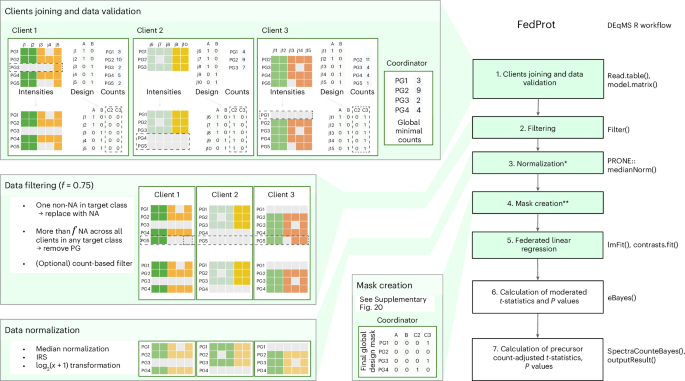
Steps that involve federated computations are shown in green. The corresponding stages of DEqMS workflow are shown on the right. Median normalization from the PRONE58 R package was used. The validation, filtering, normalization and design mask creation steps involving three clients (C1, C2 and C3) are shown on the left. PG denotes protein groups, j are sample numbers, and A and B are target classes compared during the analysis. On step 1, the PG3 value for sample j5 is replaced with NA (only one not-missing value in the client data). On step 2, the PG5 value for sample j5 is replaced with NA (one not-missing value for this PG in the target class for this client). After that, the whole PG5 group is removed from all clients because of too few nonmissing values (here, less than f = 0.75). On the design mask creation step, client 3 for PG1 is excluded because it has no data, same for PG4 of client 2; and, the client 3 became the new reference client and also excluded from computation (PG3 is missing in client 1). See Methods and Supplementary Methods for more details. *The normalization step is optional and could be turned off by the coordinator. In case of TMT data, for filtering out decoys, contaminant and reverse protein groups are required. The normalization by median across all centers and IRS inside each center can be performed during a FedProt run. **The step is for the federated approach only. Created with BioRender.com.
In the first step, \(k > 2\) FedProt clients join the analysis initialized by the coordinator and validate their data. From each client \({c}^{i}\), where \(i=1,\ldots ,k\), FedProt requires two tab-separated (.tsv) files:
(1)
A protein intensities matrix \({Y}_{{raw}}^{i}\) containing the intensities of \({n}^{i}\) proteins or protein groups (rows) detected in \({m}^{i}\) samples (columns). Protein groups detected only in a single sample in the cohort are replaced with NA (missing value), to avoid exchanging individual-level data in the next steps and protect data privacy.
(2)
A design matrix \({X}^{i}\) specifying which columns of the intensity matrix belong to which experimental conditions or groups. In the design matrix, each experimental condition or group should be coded as a binary variable, with 1 if the sample belongs to the group and 0 if not. For example, if we compare conditions A and B, the design should contain both A and B columns with 0 or 1 for each sample. Optionally, the design matrix can contain columns representing the covariates. The names of target class columns and covariates in local design matrices must match the names specified by the coordinator during the initialization of the study.
(3)
An optional file—a matrix with the number of quantified precursor peptides for each protein group \({\Pr }_{\min }^{i}\). For each client, one value per protein group is required. For example, it can be found in the Precursor.Ids column in the DIA-NN report, or in the Peptide.IDs column in the MaxQuant report. If the clients do not have \({\Pr }_{\min }^{i}\), the computation will be completed after the sixth step, with no precursor peptide count adjustment.
Clients join the server, and during the first step FedProt ensures that all the clients provide all necessary inputs. Each client sends to the server information about the number of samples \({m}^{i}\), the peptide-to-protein minimal counts \({\Pr }_{\min }^{i}\) and the list of protein groups \({P}^{i}\) they have. The server uses each client’s \({\Pr }_{\min }^{i}\) matrices to get the global minimal number of quantified precursor peptides across all samples from all clients for each protein group, \({\Pr }_{\min }^{i}\); this is needed for the last step.
For each client \({c}^{i}\), the server updates the set of all detected protein groups \(P\) across all clients participating in the analysis. After that, clients receive from the server the set of all protein groups \(P\), and the list of variables \(v\) accounted for in the model (target classes, list of cohorts and, optionally, covariates). If the protein group is not in the client data, it is created and filled with NAs in the \({Y}_{{{\mathrm{raw}}}}^{i}\).
The list of variables \(v\) is used to update the design matrix \({X}^{i}\) and include columns representing batches to account for batch effects. Each client updates the design matrix \({X}^{i}\) and adds cohort effects to it based on the list of variables \(v\). The cohort effects are added as binary columns, where the first client \({c}^{1}\) represents the reference batch, as in limma, and the corresponding column is not included in the design matrix. If the coordinator participates in the computation as a client, it becomes the first client \({c}^{1}\).
In the second step, FedProt applies filters. One of them is to filter out protein groups with too many missing values. Each client \({c}^{i}\) calculates the number of samples with missing values per target class for each protein group and shares it with the server. The server computes global fractions of missing values per protein group and target class and the protein groups not detected in more than \(f\) fraction of each target class samples in any target classes are removed from \(P\). The value of \(f\) is set to 0.8 by default and can be adjusted by the coordinator. The next optional filter removes protein groups supported by only one peptide precursor; this filter can be enabled by the coordinator. Another filter converts rows to missing values (NA) if all but one value are missing in samples for a given design column; this protects sensitive data sharing during computations and is done before the first above-described filter.
The next step is the normalization step; this step is optional and depends on the coordinator settings. Currently, two types of normalization are implemented. The first one is median normalization. For that, each client calculates the median intensity across all protein groups for each sample \(j\) in their dataset, \({{{\mathrm{Med}}}}_{j}^{i}\). Clients’ median average \({\overline{{{\mathrm{Med}}}}}^{i}\) is sent to the coordinator. The coordinator then calculates the global weighted mean of clients’ sample medians:
$$\overline{{{\mathrm{Med}}}}=\frac{{\sum }_{i=1}^{k}{\overline{{{\mathrm{Med}}}}}^{\;i}\times {m}_{i}}{{\sum }_{i=1}^{k}{m}^{i}}.$$
Once the global median mean is computed, the coordinator broadcasts it to clients. Each client’s jth sample intensity values are adjusted on the basis of this value:
$${Y}_{\text{norm},\;j}^{\;i}=\frac{{Y}_{{{\mathrm{raw}}},\;j}^{\;i}}{{{\mathrm{Med}}}_{j}^{i}}\times \overline{{{\mathrm{Med}}}}.$$
The second normalization is internal reference scaling (IRS) using in silico references. This normalization is suitable when one client has multiple TMT plexes and is conducted within each cohort. For each TMT plex, an in silico reference sample \({\text{Ref}}_{\text{plex}}\) is created taking the mean value for each protein group across all samples in the TMT plex. Then, the geometric mean for each protein across all clients’ in silico references is computed as
$$\text{GM}=\left(\exp \frac{1}{{{d}}}\mathop{\sum }\limits_{1}^{{{d}}}\log \left({\text{Ref}}_{\text{plex}}\right)\right),$$
where \(d\) is the total number of plexes in the ith client.
Using \({\text{Ref}}_{\text{plex}}\), the scaling factor \({\text{SF}}_{\text{plex}}\) is calculated for each protein in each TMT plex as the ratio of the geometric mean to the in silico reference for that plex:
$${\text{SF}}_{\text{plex}}=\frac{\text{GM}}{{\text{Ref}}_{\text{plex}}},$$
and normalized intensities are computed by multiplying with the scaling factor.
Both implemented normalization methods should be done on non-log-transformed data, so after this step, \({\log }_{2}(x+1)\) log transformation is applied if required by the coordinator in the analysis settings.
To make possible the analysis of all protein groups available, we used a design matrix mask \(D\) for the next steps. The mask has the number of columns equal to the design matrix and rows for each protein group. The mask creation is described in more detail in Supplementary Methods.
In the fifth step, for each protein group in \(P\), FedProt fits a linear model in a federated fashion, following the approach described by Karr et al.48, assuming that protein group intensity \(Y\) can be modeled as
$${\rm{Y}}={\rm{X}}{{\beta }}+{{\epsilon }},$$
where \(X\) is the global design matrix and \(\epsilon\) is random noise. The coefficients \(\beta\) defining the impact of each variable in the design matrix \(X\) on the observed intensities can be estimated as
$$\hat{\beta }={\left({X}^{T}X\right)}^{-1}{X}^{T}Y,$$
and the unscaled standard deviations \({\text{st.dev}}_{\text{unscaled}}\) or the coefficients \(\hat{\beta }\) can be estimated as
$${\text{st.dev}}_{\text{unscaled}}=\sqrt{{{\mathrm{diag}}}\left({\left({X}^{T}X\right)}^{-1}\right)}.$$
To avoid sharing \({X}^{\;i}\) and \({Y}^{\;i}\) containing sensitive patient-level data that would be necessary to obtain \(X\) and \(Y\), \({X}^{T}X\) and \({X}^{T}Y\) terms of the equation can be computed through the summation of local \({({X}^{\;i})}^{T}{X}^{\;i}\), and \({({X}^{\;i})}^{T}{Y}^{\;i}\) computed by clients:
$${X}^{T}X=\mathop{\varSigma }\limits_{i=1}^{k}{({X}^{i})}^{T}{X}^{i}$$
$${X}^{T}Y=\mathop{\varSigma }\limits_{i=1}^{k}{({X}^{i})}^{T}{Y}^{i},$$
\({({X}^{\;i})}^{T}{X}^{\;i}\) and \({({X}^{\;i})}^{T}{Y}^{\;i}\) do not reveal any patient-level data and can be shared with the server. To minimize the rare risk of data exposure, clients independently detect and resolve issues during the data validation step (protein groups detected in only one cohort sample are replaced with NA; Fig. 3, step 1).
On this step design mask \(D\) is used to exclude columns and rows corresponding to missing values from \({X}^{T}X\) and columns from \({X}^{T}Y\). This is necessary to exclude from the calculations for a particular protein the values belonging to a particular column from the design \(X\), because these cohorts do not have values (all are NAs). \(D\) usage allows us to simulate behavior of the lmFit function from the limma R package when working with missing values in data.
To minimize the risk of reconstruction attack, \({({X}^{\;i})}^{T}{X}^{\;i}\), \({({X}^{\;i})}^{T}{Y}^{\;i}\) and any local computation result shared with the aggregating server are protected by additive secret sharing30. In brief, each client generates \(n\) randomly sampled noise masks, \({r}_{1},\ldots ,{r}_{n}\), as equally distributed random values and calculates corresponding noisy data as (\(M-{r}_{1}-\ldots -{r}_{n}\)). This noisy data, alongside the noise masks (divided into \(n\) pieces in total), is communicated with other computational parties via a relay server, ensuring that no party receives more than one piece (one data piece and one noise piece) from any specific client. The data pieces are encrypted with each party’s public key to ensure the data cannot be intercepted. Once the encrypted pieces are received, each party decrypts and sums the received data, then sends the reencrypted received sums to the coordinator again via the relay server. The coordinator gets the summed parts and, in case of sending \({({X}^{\;i})}^{T}{X}^{\;i}\) and \({({X}^{\;i})}^{T}{Y}^{\;i}\), obtains the global coefficients \(\hat{\beta }\).
During the additive secure aggregation process, the noises cancel out due to their additive nature, resulting in the correct global aggregation of local parameters without any noticeable impact on the final outcome compared with nonsecure aggregation. This cancelation mechanism preserves data privacy, as the individual intermediate results that remain are not revealed to the coordinator or any other parties. By increasing the number of parties, the risk of collusion to reconstruct the clients’ intermediate results will be further reduced. To simplify the technical aspects of communicating data, FeatureCloud34 passes all data through the relay server that cannot decrypt the data (see details in Supplementary Methods).
Global estimated coefficients \(\hat{\beta }\) are shared with the clients, who use it to calculate the local sum of squared errors \({{\rm{SSE}}}^{{{i}}}={\sum }_{{\rm{j}}}^{{{{m}}}_{{\rm{i}}}}{({{{y}}}_{{{j}}}^{{{i}}}-\hat{y}_j^i)}^{2}\), where \({\hat{y}}_{j}^{i}\) is the jth component of \({\hat{Y}}^{i}={X}^{i}\hat{\beta }\). The server aggregates local sum of squared errors \({{{\mathrm{SSE}}}}^{i}\) to the global sum of squared errors SSE,
$${{\mathrm{SSE}}}=\mathop{\varSigma }\limits_{i=1}^{k}{{{\mathrm{SSE}}}}^{i}$$
and computes the residual standard deviations \(\sigma\) as follows:
$$\sigma =\sqrt{\frac{{{\mathrm{SSE}}}}{m-\left|v\right|}},$$
where \(m={\varSigma }_{i}^{k}{m}^{i}\) is the number of samples with detected protein group and \(\left|v\right|\) is the number of variables in the design matrix except masked with the design matrix mask. In this step, a design mask is applied to ensure that missing values are handled correctly.
The sixth step is performed solely on the server side. Given a set of target classes, the contrast is defined as linear combinations of conditions or target classes in a design matrix \(X\) and represented as a contrast matrix \(K\). The fitting of these contrasts implies the application of the contrast matrix to the regression coefficients \(\hat{\beta }\) and covariance matrix of these coefficients \(C\) as follows:
$$\hat{\beta }^{\prime} =\hat{\beta }K$$
$$C^{\prime} ={K}^{T}{CK}.$$
The standard deviations \(\text{st.dev}\) for the coefficients are also updated during this step. Specifically, the covariance matrix \(C^{\prime}\) is scaled by its diagonal to become the correlation matrix, on which the Cholesky decomposition is performed, and the result is then used to transform and scale the \(\text{st.dev}\) and get the \({\text{st.dev}}^{{\prime} }\). This replicates the implementation of the contrasts.fit function from the limma R package49.
Further computations performed on the server side replicate eBayes from limma50 and require only global \(\hat{\beta }^{\prime}\), \({\sigma }^{2}\) and \({\text{st.dev}}^{{\prime} }\). This step starts with moderated t-statistic calculation. For that, variance shrinkage is performed to stabilize the variance estimates across genes. Given a vector of sample variances \({\sigma }^{2}\) and their associated degrees of freedom \({\text{df}}_{\text{residual}}\), the empirical Bayes approach fits an F distribution to estimate the parameters of the prior distribution.
Using the estimated priors (variance \({{\rm{\sigma }}}_{\text{prior}}^{2}\) and the degrees of freedom \({\text{df}}_{\text{prior}}\)), the posterior variances \({\sigma }_{\text{post}}^{2}\) were calculated as a weighted average of the prior and sample variances as follows:
$${{\rm{\sigma }}}_{\text{post}}^{2}=\frac{{\text{df}}_{\text{residual}} {{\rm{\sigma }}}^{2}+{\text{df}}_{\text{prior}}{{\rm{\sigma }}}_{\text{prior}}^{2}}{{\text{df}}_{\text{residual}}+{\text{df}}_{\text{prior}}}.$$
After this, the moderated t-statistic t and B-statistic \(B\) are computed as
$$t=\frac{{\beta }^{{\prime} }}{{\text{st.dev}}^{{\prime} }}\times \frac{1}{\sqrt{{\sigma }_{\text{post}}^{2}}},$$
where \(\beta {\prime}\) represents the estimated coefficients (logFCs) and \({\text{st.dev}}^{{\prime} }\) denotes the unscaled standard deviations of the coefficients, and
$$B=\log \left(\frac{p}{1-p}\right)-\frac{\log (r)}{2}+k,$$
where \(p\) is the proportion of differentially expressed genes, \(r\) is the ratio of the variance of the gene to the prior variance and \(k\) is a function involving the moderated t-statistics and the degrees of freedom. The B-statistic represents the log-odds of differential expression.
Finally, the BH procedure51 is applied to compute adjusted P values. In the result of this step, a feature table that provides moderated t-statistics, logFCs, confidence intervals and adjusted P values is generated. The FedProt workflow can be completed after this step without precursor peptide count adjustment.
The last, seventh step replicates spectraCounteBayes from the DEqMS method33, which estimates different prior variances for proteins quantified by different numbers of peptide precursors and calculates peptide count-adjusted moderated t-statistics and P values. The server uses the minimal number of quantified precursor peptides across all samples for each protein for estimating the variance of log-counts and fitting a regression model. As a result, the system outputs a final table with statistical measurements for each feature corrected to the number of precursors.
The resulting table is saved on a server and sent to the clients. This approach in FedProt allows us to obtain the same result as what centralized pooled data analysis would yield while implementing strong privacy-preserving measures.
The FedProt user-friendly implementation is accessible as a FeatureCloud app (https://featurecloud.ai/app/fedprot), making privacy-preserving differential protein abundance analysis available to a broad community of biomedical experts. In addition, the FeatureCloud platform supports the integration of multiple applications into workflows. This allows FedProt to be combined with other privacy-preserving analysis tasks (for example, federated singular value decomposition52 and clustering techniques such as k-means clustering53 available as FeatureCloud apps).
Meta-analysis approaches
To evaluate FedProt’s accuracy in comparison with meta-analyses, we used three classes of meta-analyses: effect size combination methods (the REM54,55 from the metaVolcanoR package56 v.1.12.0), P value combination methods (Fisher’s method19 from the metaVolcanoR package56 v.1.12.0 and Stouffer’s method20 from the the MetaDE55 package v.2.2.3) and nonparametric rank combination methods54,57 (Rank Product method from the RankProd24 R package v.3.24.0).
For all chosen meta-analysis methods except REM, the global FC was calculated as the mean of local FCs, producing the same values. Consequently, only Fisher’s method and REM results were utilized for the evaluation of logFCs.
Human serum dataSample preparation
For FedProt evaluation, we were using a TMT dataset of 60 independent human blood serum samples, comprising 30 from patients with primary FSGS and 30 from healthy controls. Written consent for anonymized data retrieval and storage was obtained. The local ethics committee of the Friedrich-Alexander Universität Erlangen–Nürnberg provided approval for the nephrological biobank of the Klinikum Bayreuth (ethics approval code 264_20 B) and the proteomics analysis (ethics approval code 221_20 B). Approval to perform MS of serum samples was given by the ethics committee of the Friedrich-Alexander Universität Erlangen–Nürnberg (ethics approval code 182_19 B).
The samples were separated into three groups, each containing ten healthy and ten FSGS samples, blinded and distributed to three studies centers by the clinical partners (Supplementary Methods). The samples were prepared and measured by independent researchers (that is, in three different LC–MS/MS locations on different days) in a blinded manner using the same protocol until complete data collection. Patient group allocations were disclosed for data analysis.
Sample preparation and LC–MS/MS measurement
Samples were prepared by three independent scientists applying a harmonized protocol. TMT-labeled samples were combined into six sets, each containing five healthy, five FSGS and one common reference sample.
MS data were acquired in three independent research centers using their preferred instruments and corresponding parameter setups (Table 1B). More details on the LC–MS/MS measurement protocols are provided in Supplementary Methods.
Raw data analysis
Raw mass spectra were uniformly preprocessed and quantified using MaxQuant (v.2.4.2) software35 separately for each center. The analysis was conducted with default settings unless otherwise specified. Experimentally acquired mass spectra were searched against a human reference proteome (Uniprot, v.2023_05, reviewed/Swiss-Prot entries only, 20,418 protein sequences). Trypsin/P was set as protease (specific mode) allowing a maximum of two missed cleavages. Carbamidomethylation of cysteine was set as a fixed modification, while oxidation of methionine and acetylation of protein N-terminus were allowed as variable modifications. A minimum of two peptides including one unique peptide were required for protein inference controlling the false discovery rate to
Data filtering and preprocessing
For protein intensity matrices, MaxQuant reports were independently preprocessed filtering out decoy, contaminant and modification site-only entries. The column ‘Majority.protein.IDs’ was used for protein group names, and within a group, proteins were sorted alphabetically. This additional sorting allows a better intersection of independently processed data. As FedProt uses in silico references in the TMT analysis workflow, six reference samples were removed from the dataset before analysis.
Protein groups supported by a single peptide were removed during the central DEqMS analysis. Raw intensities were normalized to the median across all data (from PRONE58 R package v.1.0.4, https://github.com/daisybio/PRONE), followed by IRS within each center with an in silico reference—the mean of all samples for each pool in the center (modified IRS from PRONE). Similar filters and normalizations are also implemented in FedProt. Quality control was performed in R (Supplementary Figs. 1 and 10B).
Bacterial dataset creationSample preparation
We evaluated FedProt using a LFQ dataset of 118 samples generated from E. coli MG1655 (DSM 18039) cultures. Samples were shipped on dry ice either as lysates or as cell pellets (Table 1A; for more details, see Supplementary Methods).
Laboratory A and laboratory B received cell pellets, while others (C, D and E) received already lysed cells. Each laboratory received 20 (19 for laboratories B and C) unique and 4 shared (quality control) samples, 12 (11) samples per condition. One sample was lost during shipment, and one more was excluded during quality control of MS results. Each of the four quality control samples was generated by aliquoting one starting sample, meaning they are technical replicates.
Sample preparation and LC–MS/MS measurement
Laboratories A, B and C performed bacteria cell lysis separately, and laboratories E and D used cell lysates prepared by laboratory C, sent and diluted. Each laboratory used slightly different protocols for protein digestion, peptide purification and preparation for MS.
MS data were acquired in five independent research centers using their preferred sample preparation (in case of cell pellets), MS measurement protocols, instruments and corresponding parameter setups (Table 1A). More details on the LC–MS/MS measurement protocols are provided in Supplementary Methods.
Raw data analysis
Raw mass spectra were uniformly preprocessed and quantified using DIA-NN36 (https://github.com/vdemichev/DIA-NN), v.1.8.1 in a separate run for each laboratory. The analysis was conducted with default settings unless otherwise specified. When analyzing the robustness against preprocessing variability, Spectronaut v. 17.5 and v.17.2 and DIA-NN v.1.8.0 and v.1.8.1 were used (Supplementary Table 4). An in silico spectral library was generated in each DIA-NN and Spectronaut run from the E. coli MG1655 (taxID 83333) protein sequence database (Uniprot UP000000625, 4,448 entries) provided via a FASTA file (no preexisting spectral library was utilized).
The analysis was carried out in ‘any LC (high-accuracy)’ mode. Two missed cleavages and a maximum of two variable modifications per peptide were allowed: acetylation of protein N-termini and oxidation of methionine. Minimum precursor m/z was set to 360. MBR was enabled. The data were reanalyzed utilizing a deep-learning-generated spectral library to refine the results. For specific parameters on the setup of the DIA-NN searches, see Supplementary Table 6.
Data filtering and preprocessing
Protein quantities were obtained from the MaxLFQ59 algorithm implemented in DIA-NN v 1.8.1 and extracted from reports using the diann v.1.0.1 R package. For protein intensity matrices, DIA-NN outputs were filtered using the following criteria: Lib.Q.Value ≤0.01 and Lib.PG.Q.Value ≤0.01. As MaxLFQ protein quantities are already normalized, no additional normalization was executed during preprocessing or implemented in FedProt.
Quality control was performed in R (Supplementary Figs. 1 and 11), one sample from laboratory C’s dataset was excluded after quality control due to being an outlier (Supplementary Fig. 12).
Simulated data
To generate simulated data, we used the approach proposed in ref. 37:
$${{\rm{y}}}_{{\rm{pj}}} \approx \left\{\begin{array}{lll}{\mathscr{N}}\left({\mu }_{p},{\sigma }_{p}^{2}\right) & \text{w.p.} & (1-{\pi }_{p})\\ {\mathscr{N}}\left({\mu }_{p}+\Delta \mu ,{\sigma }_{p}^{2}\right) & \text{w.p.} & {\pi }_{p}\end{array}\right.,$$
where \({y}_{{pj}}\) represents the intensity for pth protein, \(p=1,\ldots ,n\), from jth sample, \(j=1,\ldots ,m\).
Protein intensity \({y}_{{pj}}\) is modeled from mixture distribution, where \({\pi }_{p}\in [\mathrm{0,0.5})\) is the outlier proportion. Outliers could be differentially abundant proteins or technical errors. We did not add a sample effect to our model because we simulated data after the MaxLFQ method59, which contains the normalization step eliminating it. The protein population distribution parameters were generated separately for each protein, means \({\mu }_{p}\) were from \(N(\mathrm{0,2})\) and variances \({\sigma }_{p}^{2}\) were from an inverse gamma distribution.
We adapted the sim.dat.fn function from the RobNorm package37 v.0.2.0, with modifications to the inverse gamma distribution parameters (the shape parameter of 2 and scale parameter of 3). Parameter \(\Delta \mu\) was used to represent a shift in a differentially regulated block, to generate up- or downregulated proteins. The protein in the block has a chance, derived from a binomial distribution with a success probability of 0.8, of undergoing a shift. \(\Delta \mu\) was used to represent a shift in a differentially regulated block, to generate up- or downregulated proteins.
We generated the data without batch effects first, with 6,000 proteins and 600 samples, 300 each in conditions A and B. The block consisting of 200 proteins differentially abundant between conditions A and B was obtained using \(\Delta \mu = 1.25\). To simulate the effects of unknown covariate, a block of 150 proteins each was generated, with \(\Delta \mu = 1.25\), and randomly assigned to samples in class B. The proportion of samples in class B with unknown covariate is presented in Supplementary Table 2.
To simulate a multicenter study, we then randomly split the data into three cohorts (C1, C2 and C3) and added batch effects. To investigate the effect of data imbalance on method performances, data were split into cohorts twice: once with equal cohort sizes and frequencies of conditions A and B, and once with unequal cohort sizes and condition frequencies (see Supplementary Table 2 for details).
To simulate batch effects in our data, we utilized the ComBat model38 designed for removing batch effects:
$${y}_{{pji}}={y}_{{pj}}+{\gamma }_{{pi}}+{\delta }_{{pi}}{\epsilon }_{{pji}},$$
where \(i=1,\ldots ,k\), and \(k\) is the total number of batches, errors \({\epsilon }_{{pji}}\) are normally distributed \(N(\mathrm{0,1})\), additive batch parameter \({\gamma }_{{pi}}\) is drawn from normal distribution and multiplicative batch parameter \({\delta }_{{pi}}\) is drawn from inverse gamma distribution. For simulation, we used \({\gamma }_{p1}\approx N(\mathrm{0,1})\) for additive batch effects and \({\delta }_{p1}\approx {IG}(\mathrm{3,2})\) for multiplicative batch effect for the first batch, \({\gamma }_{p2}\approx N(\mathrm{0.2,0.5})\) and \({\delta }_{p2}\approx {IG}(\mathrm{2.5,1})\) for the second batch, and \({\gamma }_{p3}\approx N(-\mathrm{0.2,1.5})\) and \({\delta }_{p3}\approx {IG}(\mathrm{4,0.5})\) for the third batch.
Missing values were introduced to the data using the approach described previously39, with a missing value rate of 0.2 and a missing-not-at-random rate of 0.5, resulting in a total of 20% missing values in the dataset.
Data analysis
Data after quantification and preprocessing were analyzed in R v.4.2.0. Batch effects correction and plots were done using the following R packages: limma v.3.54.2, data.table v.1.14.8, gridExtra v.2.3, patchwork v.1.1.2, reshape2 v.1.4.4, matrixStats v.1.3.0 and tidyverse v.2.0.0 (includes ggplot2 v.3.4.2, dplyr v.1.1.4, purrr v.1.0.2, readr v.2.1.4 and tidyr v.1.3.1).
Filtering based on the number of missing values per class was done using the 80% threshold, the same as the FedProt default value. For bacterial datasets, the transformation of rows with only one non-NA value per subset of samples for a design column to NA is disabled for evaluation. For the TMT dataset, median normalization from the PRONE58 package v.1.0.4 was used (https://github.com/daisybio/PRONE).
Differential protein abundance in centralized analysis was tested with a two‑sided moderated t‑test (with empirical Bayes and with BH adjustment for P values) using DEqMS v.1.16.0 (R 4.2.0). We used log2FC, exact BH‑adjusted P values and full output tables for the bacterial and human serum datasets (provided in Supplementary Table 7). FedProt’s adjusted P values used for evaluation using the bacterial and human serum datasets are count-scaled BH-adjusted P values, similar to what DEqMS calculates. Before log transformation of adjusted P values, a small value (1 × 10−300) was used to replace 0 in REM results for the bacterial dataset. For evaluation using the simulated dataset, BH-adjusted P values were not scaled using counts, because we did not simulate spectra counts data.
FedProt implementation on the FeatureCloud platform was evaluated using Python library FeatureCloud v.0.0.32, with rpy2 v.3.5.11 Python library inside the app Docker container (Docker v.27.1.2). For the meta-analyses, we used MetaDE55 v.2.2.3, metaVolcanoR56 v.1.12.0 and RankProd24 v.3.24.0 R packages. The results of DEqMS runs in each center or laboratory separately were used as input data for meta-analysis methods.
Evaluation was done using Python using pandas v.2.2.2, numpy v.2.0.0, scipy v.1.14.0, scikit-learn v.1.5.0 and statsmodels v.0.14.2 libraries. For upset plots, Python upsetplot library v.0.9.0 was used (https://upsetplot.readthedocs.io/en/stable/). For other plots, matplotlib v.3.8.4 and seaborn v.0.13.2 packages were used. SMPC was enabled during the evaluation.
To investigate the impact of including batch effects in the design, the data were preprocessed in the same way, depending on the dataset. The difference lay in incorporating batch information into the design during the analysis or correcting the data beforehand (after preprocessing) and then performing the analysis without including this information in the design.
Reporting summary
Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.