La clé secrète de L’Homme de Vitruve viendrait-elle d’être découverte par un dentiste ? Pendant plus de 500 ans, le système géométrique utilisé par Léonard de Vinci (1452–1519) pour établir la relation précise entre le cercle et le carré dans ce fameux dessin à la plume, encre et lavis sur papier réalisé vers 1490, est demeuré un mystère. Jusqu’à la publication le 26 juin dernier, dans la revue académique Journal of Mathematics and the Arts (reprise le 18 juillet par ScienceAlert), d’une hypothèse intéressante formulée par un dentiste londonien, Rory Mac Sweeney…
Le célèbre dessin représente les proportions idéales du corps humain, parfaitement inscrit dans un cercle, dont le centre correspond à son nombril, et dans un carré, au centre duquel se trouvent ses organes génitaux. Conservé à la Gallerie dell’Accademia de Venise, il est devenu l’emblème de l’humanisme de la Renaissance, qui place l’homme au centre de l’univers, comme « mesure de toute chose », et cherche à étudier le monde sous toutes ses coutures pour en comprendre le fonctionnement.
Pour le réaliser, Léonard de Vinci s’est penché sur le traité De architectura, rédigé au Ier siècle avant J.-C. par un architecte romain, Marcus Vitruvius Pollio dit Vitruve, qui affirmait qu’un être humain aux proportions parfaites pouvait s’inscrire au millimètre près, et simultanément, dans un cercle et dans un carré. Ce que l’artiste et inventeur italien de la Renaissance a réussi à traduire en dessin. Mais quel système mathématique a-t-il utilisé pour y parvenir ?
Une question de triangle
De nombreuses théories ont été avancées au fil des années. La plus populaire étant que Léonard se serait appuyé sur le nombre d’or, surnommé « la divine proportion », présente dans la nature et consistant en une proportion entre deux longueurs, égale à 1,618 – proportion qui s’obtient lorsque les deux longueurs en question, a et b, peuvent former l’équation suivante : (a + b) / a = a / b. Sauf que cette mesure ne s’applique pas exactement à L’Homme de Vitruve : on observe sur le dessin une déviation de plus de 2 % par rapport à ce chiffre, incompatible avec la précision habituelle de Léonard !
Et si la solution nous avait été expliquée depuis le début par le savant lui-même ? C’est en lisant les annotations de Léonard associées au dessin que le dentiste Rory Mac Sweeney a eu le déclic : « Si vous ouvrez suffisamment vos jambes et que vous levez suffisamment vos mains pour que vos doigts étendus touchent la ligne du haut de votre tête, l’espace entre les jambes sera un triangle équilatéral », écrivait ainsi De Vinci.
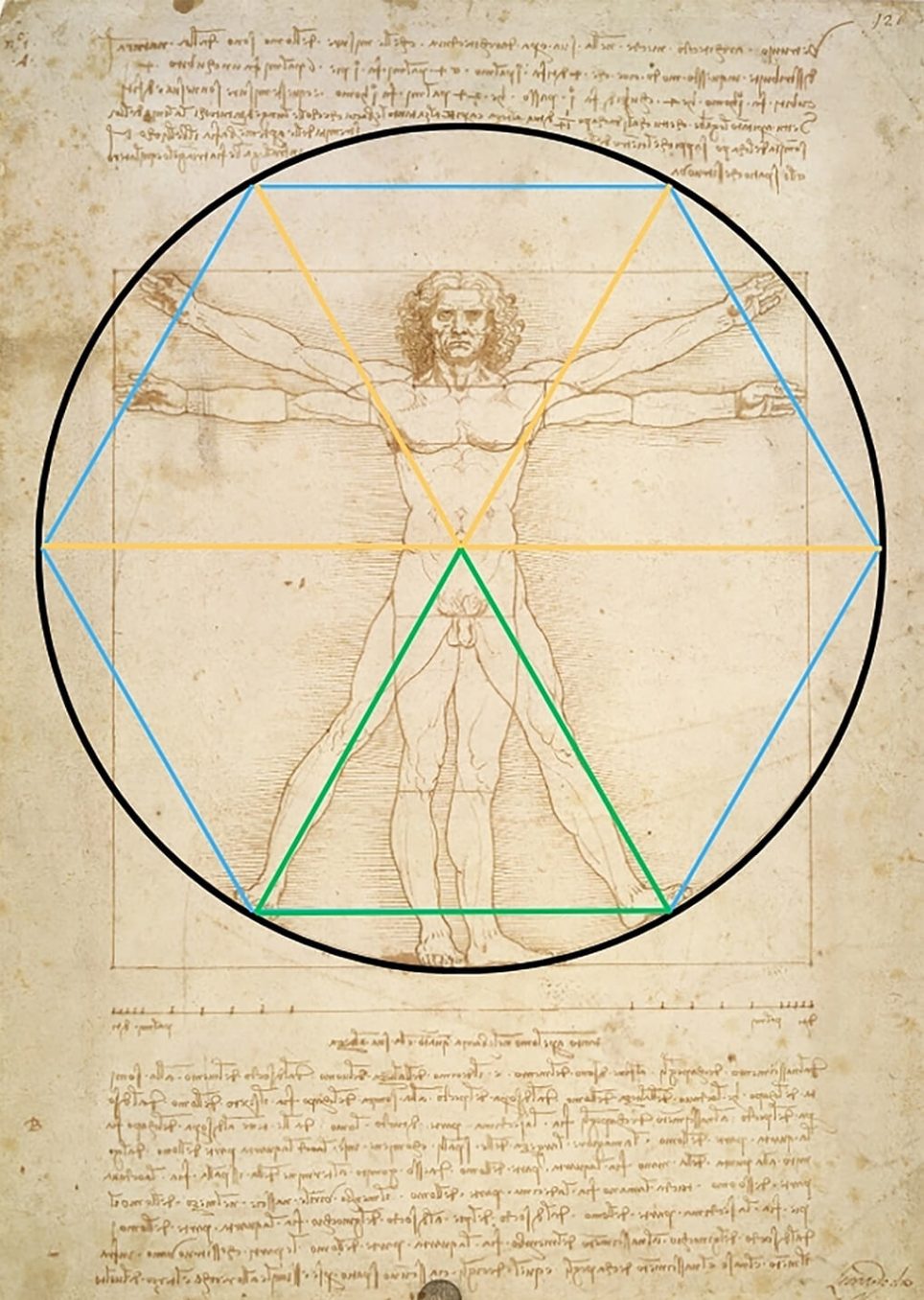
Léonard de Vinci, « L’Homme de Vitruve » et les relations géométriques optimales, vers 1490
i
Encre sur papier • 34,3 × 24,5 cm • © Bridgeman Images
Le chercheur a alors tracé un triangle équilatéral reliant le nombril et les deux pieds de L’Homme de Vitruve, puis a reproduit cette forme six fois autour du nombril pour former un hexagone s’inscrivant parfaitement dans le cercle. Il a alors constaté que le rapport entre les deux côtés de ce triangle équilatéral était d’environ 1,64 – soit le même rapport mesuré entre le côté du carré et le rayon du cercle.
À lire aussi :
Ravensburger finalement autorisé à vendre ses puzzles reproduisant « L’Homme de Vitruve » de Léonard de Vinci
L’anticipation par De Vinci de découvertes anatomiques futures
« Cela révèle que L’Homme de Vitruve de Léonard contient des principes géométriques qui anticipent la compréhension moderne de l’architecture biologique optimale. »
Mais ce n’est pas tout : Rory Mac Sweeney s’aperçoit que ce triangle équilatéral correspond au triangle de Bonwill, découvert et documenté en 1864, tracé entre le milieu des incisives et les articulations des mandibules, qui montre le positionnement idéal de la mâchoire. Car le rapport entre les deux côtés de ce triangle est de 1,633, soit une mesure pratiquement égale à celle présente dans L’Homme de Vitruve.
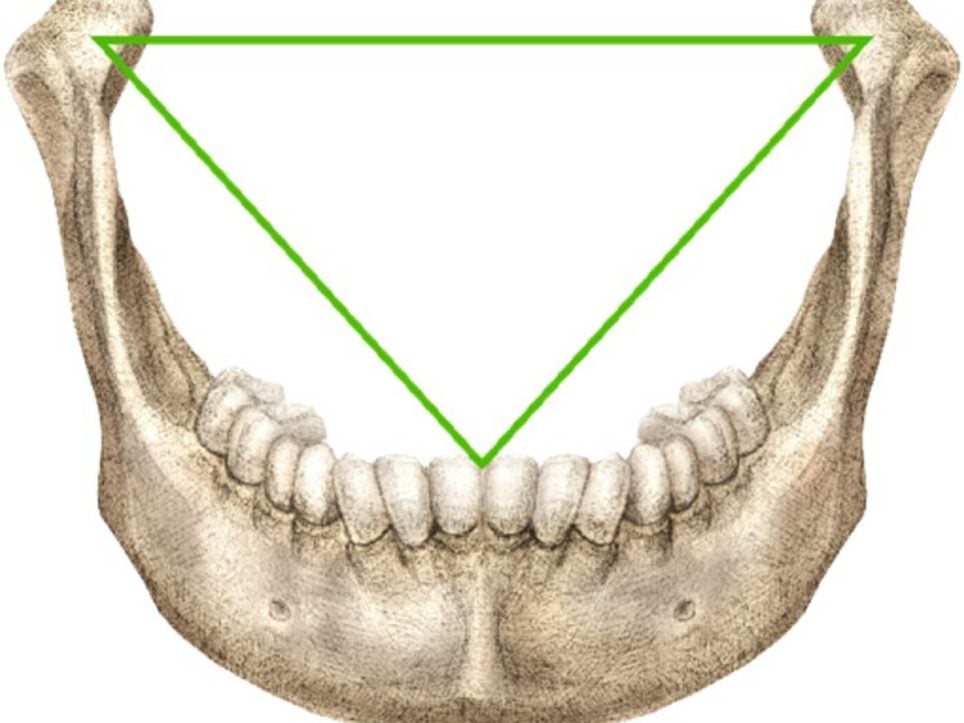
Le triangle de Bonwill en anatomie mandibulaire
i
Rory Mac Sweeney ajoute que ce rapport apparaît également « dans l’empilement optimal des sphères, les structures à tenségrité, et le Vector Equilibrium de Buckminster Fuller ». Dit aussi « cuboctaèdre », ce dernier est la seule structure géométrique dont les longueurs intérieures et extérieures sont égales, ce qui lui confère un parfait équilibre vectoriel. Enfin, ce rapport de 1,64 se retrouve aussi dans plusieurs mesures anatomiques modernes exclusivement présentes dans le corps humain, et notamment dans l’architecture du crâne.
« Cela révèle que L’Homme de Vitruve de Léonard contient des principes géométriques qui anticipent la compréhension moderne de l’architecture biologique optimale […], et qu’il y a des rapports mathématiques constants encodés dans les formes biologiques », conclut le dentiste ; avant d’ajouter que cette œuvre « témoigne de la perspicacité de Léonard, qui avait compris, des siècles avant que la science moderne ne puisse les valider, des vérités fondamentales sur la nature mathématique du monde, que les proportions humaines sont le reflet de principes mathématiques qui régentent l’organisation spatiale optimale dans tout l’univers ». Une théorie séduisante, accueillie avec intérêt par la presse scientifique depuis son dévoilement.
À lire aussi :
Ce que vous ne saviez (peut-être) pas sur Léonard de Vinci
