The behaviour of light within lasers and other photonic devices presents a long-standing challenge for physicists, as the underlying equations governing these systems are notoriously difficult to solve. Gian-Luca Oppo from the University of Strathclyde and colleagues address this challenge by employing computational physics to model a wide range of devices, including lasers with varying parameters and complex resonators. Their work demonstrates how numerical simulations can accurately predict and explain a diverse array of nonlinear phenomena, from stable light patterns to chaotic behaviour and even the emergence of rogue waves. This research is significant because it establishes a strong link between theoretical modelling and experimental observations, with potential applications spanning ultrafast optical communications, precision timing technologies, and the development of future quantum systems.
Cavity Solitons, Patterns, and Nonlinear Optics Foundations
This comprehensive collection of references details research into nonlinear optics, specifically focusing on cavity solitons, frequency combs, pattern formation, and related phenomena. Researchers have extensively studied the emergence of spatial and temporal patterns, including Turing patterns and roll patterns, and the role of instabilities in shaping these complex structures. Investigations also explore the formation and dynamics of domain walls and topological solitons, fundamental building blocks for more complex structures and frequency comb generation. Scientists have developed techniques like dual-comb spectroscopy for precise measurements and explored methods for locking domain walls to enhance comb stability, investigating the potential of quantum interference to control and enhance frequency comb generation. This body of work emphasizes the study of nonlinear dynamics in optical systems, leading to the formation of complex structures and patterns, and demonstrates the importance of spatial and temporal pattern formation driven by nonlinear interactions.
Numerical Investigation of Nonlinear Optical Dynamics
This research pioneers a comprehensive numerical investigation of nonlinear dynamics across a range of optical systems, building upon the earliest laser simulations performed in the 1960s. Researchers systematically model and solve equations governing lasers, Kerr resonators, saturable absorbers, and optical parametric oscillators, revealing the emergence of complex behaviors through numerical simulations. The study employs a fourth-order Runge-Kutta method to accurately integrate nonlinear ordinary differential equations, a standard computational physics technique. By varying parameters within these models, scientists observe and characterize stability and instability phenomena, including pitchfork, saddle-node, Hopf, and Turing bifurcations, as well as bistability, oscillations, chaos, and soliton formation.
The team meticulously analyzes the dynamics of a swing pendulum, revealing how external forcing induces oscillations and period-doubling bifurcations. Through Fourier transforms, they extract power spectra to precisely determine frequency components, nonlinear shifts, and spectral broadening, providing detailed insight into the system’s response to changing parameters. To facilitate analysis of non-autonomous systems, researchers introduce an auxiliary differential equation, transforming the original equations into an autonomous system, enabling a more straightforward investigation of their behavior. Extending beyond ordinary differential equations, the study investigates Turing instabilities, crucial to pattern formation in photonic systems, modeling this instability using the Swift-Hohenberg equation to describe the emergence of spatial patterns. A linear stability analysis reveals how the system transitions from stable to unstable states as parameters are varied, demonstrating the formation of spatially modulated patterns.
Nonlinear Dynamics and Bifurcation Phenomena Revealed
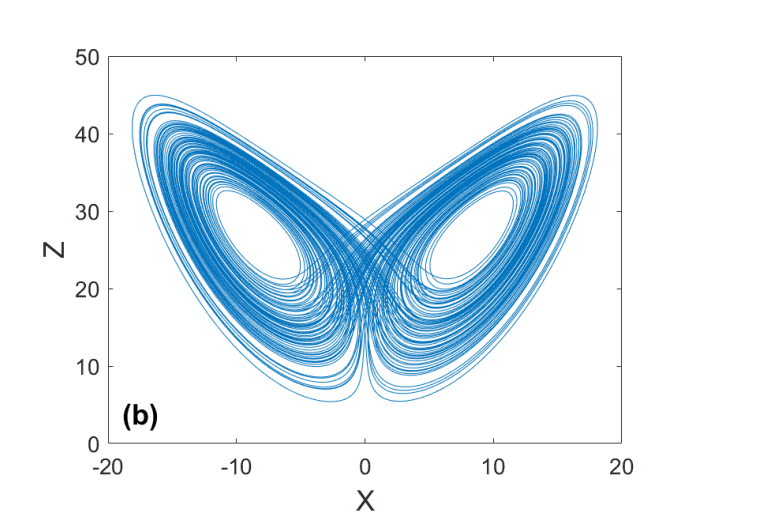
Scientists have demonstrated the complex dynamics of nonlinear systems through detailed numerical simulations and modeling, building upon the foundational work initiated with the first laser in 1960. The research team numerically solved model equations for a variety of devices, including lasers, Kerr resonators, and optical parametric oscillators, revealing the presence of stability and instability through bifurcations such as pitchfork, saddle-node, and Hopf bifurcations. These simulations uncovered a range of nonlinear phenomena, including bistability, nonlinear oscillations, deterministic chaos, Turing patterns, and solitons, all validated by laboratory experiments. Experiments with specific parameter values demonstrated high sensitivity to initial conditions, a hallmark of chaotic systems. The team further investigated period doubling cascades to chaos, observing that successive bifurcations follow a convergent series with a rate defined by the Feigenbaum number, culminating in a threshold of deterministic chaos, characterized by non-periodicity, sensitivity to initial conditions, and a continuous power spectrum. Analysis of simplified equations revealed a transition from a stable limit cycle oscillation to chaotic behavior as a control parameter was varied, confirmed by Fast Fourier Transforms showing distinct sub-harmonic peaks for the periodic orbit and a broad continuum of frequencies for the chaotic state, demonstrating the fundamental principles governing the emergence of complex behavior in nonlinear optical systems and having implications for applications in ultrafast optical communications, optical memories, and quantum technologies.
Photonic Device Modelling Validates Experiment and Predicts Behaviour
This research demonstrates the powerful synergy between computer simulation and the advancement of laser and photonic device technology, a relationship that began with the first laser in 1960. By numerically solving the model equations governing these devices, scientists have accurately reproduced and predicted a wide range of behaviors, from simple relaxation oscillations to complex spatio-temporal dynamics like solitons and frequency combs. These simulations have not only validated experimental observations but have also provided novel insights into the underlying physics of light-matter interaction and nonlinear optics. The team successfully modelled a diverse array of photonic devices, including lasers with modulated parameters, saturable absorbers, and optical parametric oscillators, revealing phenomena such as bistability, chaos, and the formation of Turing patterns, and accurately described light propagation in Kerr media and the behavior of cavity solitons, structures now widely used in generating optical frequency combs. The relatively straightforward application of standard numerical techniques, such as Runge-Kutta methods, highlights the accessibility and efficiency of this approach. While acknowledging that their work focuses on simplified model equations, and that real-world devices often exhibit more complex behaviors, this work establishes a strong foundation for continued exploration of nonlinear photonics and the development of innovative optical technologies, with potential applications spanning optical communications, neuromorphic networks, and precision measurement.