Topologically protected states in a photonic crystal can prevent backscattering of light, but creating these states requires the photonic crystal to be engineered to break time-reversal symmetry. Major strides have been taken towards this goal using a photonic crystal driven by a circularly polarized laser.
You have full access to this article via your institution.
In optical systems, true topological protection prevents backscattering of light. Writing in Nature Nanotechnology, Jin et al.1 now present convincing evidence of a planar optical system supporting Chern bands that establish topological protection — in our view, a tour de force experiment that holds the promise of entirely suppressed backscattering.
Despite the expanding pantheon of materials and devices that exhibit topological protection, perhaps none can surpass the very first example in terms of elegance of formalism, simplicity of description, and most importantly, robustness to disorder. That seminal 1980 discovery is known as the quantum Hall effect. In silicon devices in which electrons were confined to a two-dimensional plane, von Klitzing and colleagues2 showed that, under a strong perpendicular magnetic field and at low temperature, the transverse (Hall) conductance was precisely fixed — quantized — as an integer multiple of a fundamental constant of nature, namely e2/h, the quantum of conductance. This all-important integer, known as the Chern number, arises from the complex topological properties of the electronic states and it labels the energy bands of the material.
The fact of this integer quantization captures the topological protection: small perturbations to the system, including the presence of unwanted disorder in the material, cannot change the transverse conductance because there is no way to smoothly change one integer into another. As a result, the material is endowed with remarkable robustness, such that the conductance can be measured to approximately one part in a billion — a measurement that is used to define the unit of resistance, the ohm. This robustness can also be understood in terms of electronic states that remain confined to the edges of the two-dimensional system, forming quantum wires carrying electrons that can only move one way, and not the other. The deep connection between these ‘chiral edge modes’ and the Chern number that labels the energy bands — a fundamental principle known as bulk-edge correspondence — lies at the core of topological matter.
Haldane and Raghu3 later proposed that this effect was not limited to the transport of electrons, but rather could be realized for electromagnetic waves in photonic crystals as well, and the effect was demonstrated for microwave radiation4. Photonic crystals are artificially fabricated structures whose dielectric constant varies periodically in space. The challenge in realizing topologically protected states in a photonic crystal is that the system would have to incorporate magneto-optical materials in order to break time-reversal symmetry: breaking this symmetry is the only way to induce one-way edge states, because as long as time-reversal symmetry is present, there must be spatially overlapping modes moving both forwards and backwards. This challenge is a major one in the optical domain, owing to the very weak magnetic material response at high frequencies.
An alternative to using magneto-optical materials for breaking time-reversal symmetry is the so-called Floquet approach, in which the structure is actively modulated in time. This has been demonstrated in arrays of waveguides5, using a spatial direction to emulate the time coordinate giving rise to chiral edge states in the transverse plane. But the profoundly missing piece of the puzzle has been a planar optical system capable of supporting bands with non-zero Chern numbers and one-way chiral edge states in the optical domain. Such a system would solve fundamental challenges in photonics, making possible wide-bandwidth slow light6 and the mitigation of Anderson localization across platforms.
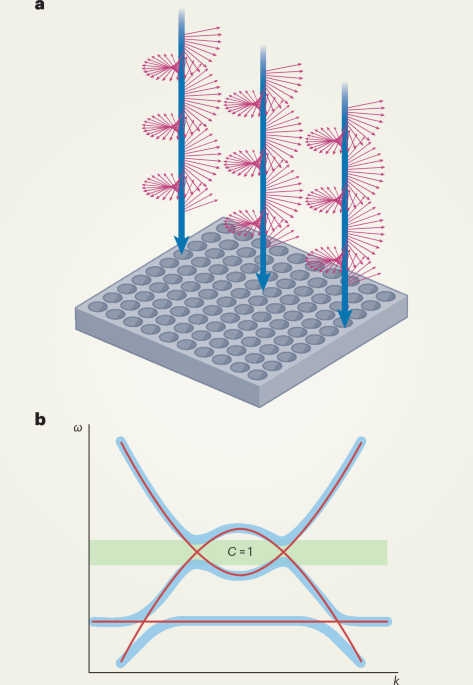
This is indeed the major development now put forward by Jin et al. They fabricate a photonic crystal in an aluminium gallium arsenide slab (Fig. 1a), with its relevant modes appearing in the near infrared. They then achieve breaking of time-reversal symmetry by temporally modulating the structure using the intrinsic second-order nonlinearity of the photonic crystal. Specifically, they inject a circularly polarized pump beam from a powerful ultrafast laser into the crystal, using the crystal’s strong nonlinear response to couple the different photonic bands (Fig. 1b). This opens up a band gap between these bands, and the authors use an analytical argument based on theoretical modelling of the system combined with the use of ‘symmetry indicators’ to identify non-zero Chern numbers in the Floquet spectrum. They also show that if the pump beam is linearly polarized instead, bands with a non-zero Chern number are not induced, consistent with time-reversal symmetry being preserved in that case.
Fig. 1: Photonic Floquet Chern bands.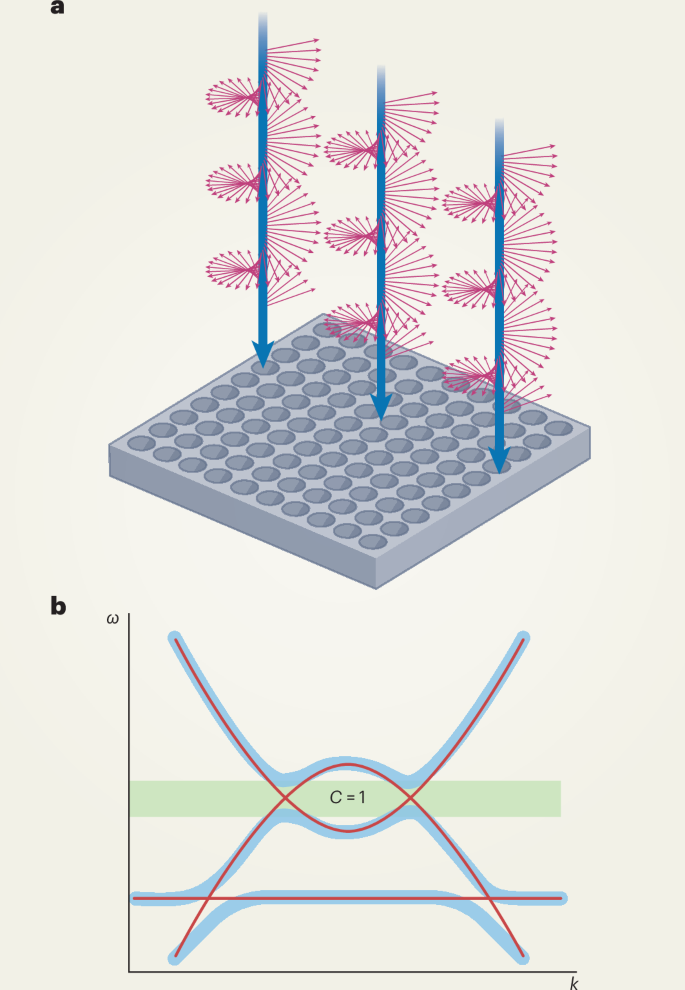
a, Using a circularly-polarized beam, a nonlinear photonic crystal is temporally modulated to break time-reversal symmetry and induce bands with non-trivial Chern numbers. b, The modulation induces coupling between the photonic bands, opening up a topological band gap.
The Floquet bands are observed using sum frequency generation into the highest frequency linear band, and the strength of this process is in turn used to show that the system has entered the strong Floquet coupling regime — namely that the splitting between bands exceed their linewidths, such that the notion of a band gap becomes meaningful. Based on these coupling strengths, Jin et al. could then theoretically calculate the apparent Floquet band structure, providing further evidence that it does indeed exhibit a topological band structure.
There are still two elements missing here, both of which are challenging but absolutely physically possible in future. First, the authors did not directly observe the anti-crossing of the Floquet bands, but rather relied on the harmonic generation efficiency to extrapolate them. Second, and more importantly, the experiment did not provide a direct experimental proof of the topological nature of the band structure, independent of theoretical modelling and arguments. According to the bulk-edge correspondence, this could be achieved in two ways: either through a direct observation of the chiral edge modes, that is, the one-way optical waveguides that are the holy grail of topological photonics4,5,7,8; or by measuring the Chern number of the bands through transport in the bulk9,10.
Nevertheless, Jin et al. have taken a bold step towards a system that offers true and complete suppression of backscattering. Although other approaches based on symmetry protection have been discussed in the literature, these can only offer protection against certain classes of just-so disorder, and very often it is not possible to dictate beforehand the type of defects and imperfections that will arise in nanofabricated structures. Indeed, it is only by doing the hard work of breaking time-reversal symmetry — as Jin et al. have done — that photonics researchers can reach the standard set by von Klitzing in that revolutionary experiment of 45 years ago.