The GST coronal adaptive optics system Cona
We developed the coronal adaptive optics system for the 1.6-m GST at the Big Bear Solar Observatory in California. The off-axis design of the GST makes it ideal for observations of faint coronal features. The secondary mirror and its mounting structure are not in the light path, which, hence, minimizes scattered light and maximizes the throughput. The clear aperture is also advantageous for adaptive optics because no pupil parts are obstructed by the mounting spider of a secondary mirror. Such spiders reduce the signal-to-noise ratio in obstructed parts of the wavefront sensor. The potential spatial discontinuity (fragmentation) in the pupil caused by spiders may lead to differential piston that is not corrected by the adaptive optics system (for example, ref. 38).
The GST is home to several state-of-the-art adaptive optics systems, including the multi-conjugate system Clear that has three deformable mirrors. The new coronal wavefront sensor is a conventional correlating Shack–Hartmann sensor (for example, refs. 10,11) and was paired with a 357-actuator deformable mirror located in a pupil image.
For the adaptive optics control, we adapted and enhanced the KAOS Evo 2 control software. This in-house developed software has roots at the GREGOR Solar Telescope39. KAOS Evo 2 is used in all GST adaptive optics systems, including the multi-conjugate system Clear40. An earlier version of the software was also used in the experiments at the Dunn Solar Telescope in 2013 (ref. 13). KAOS Evo 2 will also be used for the second-generation adaptive optics at the Daniel K. Inouye Solar Telescope when it is upgraded with ground-layer and multi-conjugate adaptive optics41.
Hα band-pass filter mounted on the wavefront sensor
A key component in the coronal wavefront sensor is the optical Hα filter. The off-disk Hα spectral radiance is typically less than 20% of the photospheric continuum radiance. Therefore, the filter band-pass must be sufficiently narrow to minimize contributions from photospheric light scattered into the line of sight by Earth’s atmosphere and the telescope optics. We used a custom narrowband, high-transmission interference filter with a band-pass width of 0.05 nm and a peak transmission greater than 50% at 656.335 nm. Maximizing the filter transmission (the throughput to the wavefront sensor) helped to preserve the available flux that can be relayed to the science instrumentation. As in any interference filter, the transmitted band-pass shifts slightly in wavelength with incidence angle. As the band-pass shifts towards the wings of the Hα emission line, the total transmitted light weakens. This creates a radial intensity gradient in the field of view or in the pupil, depending on the position of the filter15. We converged to a filter position where the pupil is mostly affected by the band-pass shift to avoid any vignetting effects in the fields of view of the subapertures. The consequent intensity gradient across the pupil implies a non-uniform signal-to-noise ratio because images in the subapertures get darker towards the edge of the pupil. The specifications of the coronal wavefront sensor are listed in Supplementary Tables 1 and 2 and compared to the photospheric on-disk sensors at the GST.
Wavefront sensor flat-fielding
The band-pass shift is also relevant for the flat-fielding of the wavefront sensor. Because the Hα line is visible on the solar disk in absorption against the black-body radiation of the photosphere, the intensity gradient caused by the shifted band-pass is inverted when pointing the wavefront sensor at the solar disk. Consequently, flat-field images acquired on-disk are not applicable off-disk15. If possible, we use flat-field frames that are created by moving the line of sight across large diffuse prominences. This is tricky because it requires the existence of respective prominences that ideally have a similar intensity level, such that the same camera gain settings can be used for the actual target prominence. Although a flat-fielded wavefront sensor typically performs better, we have also often used no flat-field correction successfully. This is possible thanks to the low photo-response non-uniformity of the camera pixels.
Updating the correlation reference for the wavefront sensor
The reference image for the correlation with the images in the subapertures is selected from a particular subaperture near the pupil centre. The reference image in the KAOS Evo 2 software is a fixed snapshot from a previous moment. As the target structure evolves, the reference image must be updated. This is a standard procedure in solar correlating Shack–Hartmann sensors. For on-disk observations, an update interval of 30–60 s is enough. Here, we used 10 s to be able to keep up with fast dynamics off the solar disk. Some very fast-evolving features require updating on the scale of seconds to prevent the control loop from becoming unstable.
Performance analysis of the adaptive optics
The KAOS Evo 2 control software can store a variety of internal data for a post-facto performance analysis. We demonstrate the performance of the adaptive optics image correction by analysing a 34-s-long control loop dataset recorded at 18:47 on 18 July 2023, during the observation of the twisted plasmoid. The frame rate in the wavefront sensor was 2,240 Hz, and its exposure time was 405 μs. Unfortunately, the camera gain settings used for these data were lost. Thus, we cannot estimate the actual light level and dark noise in the wavefront sensor at that very moment. For the wavefront reconstruction, we used a minimum mean squared error reconstruction matrix for 241 Karhunen–Loeve modes42,43.
The cross-correlation peak calculated by the KAOS Evo 2 software between the prominence images in two different subapertures was well above 95%, indicating minimal image noise. In the AO0308 Mk II wavefront sensor of the GST (Supplementary Table 1), a similar value is obtained when it is pointed at high-contrast photospheric features. When pointed at solar granulation, it is typically between 60% and 80%. Any non-common path aberrations and vibrations, if existing, in the image from VIS installed at the GST were not captured in the analysis presented.
Strehl ratio after adaptive optics correction
Supplementary Fig. 1 shows that the estimated time-variable Strehl ratio for the residual wavefront error as seen by the wavefront sensor ranges between 20% and 40%. A 20% average Strehl ratio is often considered to be sufficient to recover details near or at the diffraction limit when using image reconstruction techniques such as speckle reconstruction. If image vibration (wavefront tip and tilt) is not included in the estimation, the Strehl ratio is up to 60% to 80%. Image vibration does not contribute to image blur in sufficiently short exposures. Fast and strong image vibration that is not well corrected by the adaptive optics often originates from mechanical vibrations somewhere in the telescope. It is reasonable to disregard such effects in a performance analysis because such vibrations can be considered to be beyond the scope of the adaptive optics system.
The Strehl ratio was estimated using the Maréchal approximation:
$$S({t}_{i})\approx\operatorname{e}^{-\sum_{n}{\sigma }_{{{\rm{KL}}}_{n}}^{2}({t}_{i})},$$
(1)
where \(\sum_{n}{\sigma }_{{{\rm{KL}}}_{n}}^{2}({t}_{i})\) is the sum of the phase variances of all Karhunen–Loeve modes as reconstructed by the control software in control loop cycle ti. The uncorrected higher-order modes were neglected because they do not reduce the Strehl ratio substantially at the presented levels, if assuming a Kolmogorov spectrum. The Strehl ratio was denoised using a 2-s-long moving average.
Image vibration after the adaptive optics correction
The root-mean-squared residual image vibration at the wavefront sensor was 49 mas, which is approximately 60% of the theoretical diffraction limit at 656.3 nm. The vibration was calculated from the two-dimensional subaperture image shifts \({s}_{x}^{(k)}({t}_{i})\) and \({s}_{y}^{(k)}({t}_{i})\) in the kth subaperture at time ti according to
$${S}_{x}({t}_{i})=\frac{1}{K}\sum_{k=1}^{K}{s}_{x}^{(k)}({t}_{i}),$$
(2)
$${\sigma }_{{S}_{x}}^{2}=\frac{1}{N-1}\sum_{i=1}^{N}{\left\vert {S}_{x}({t}_{i})-\overline{{S}_{x}({t}_{i})}\right\vert}^{2},$$
(3)
$$\begin{aligned}{\sigma }_\mathrm{S}&=\sqrt{{\sigma }_{{S}_{x}}^{2}+{\sigma }_{{S}_{y}}^{2}}\\ &=\sqrt{{(17\,{\rm{mas}})}^{2}+{(45\,{\rm{mas}})}^{2}}=49\,{\rm{mas}},\end{aligned}$$
(4)
where K = 256 is the number of subapertures in the wavefront sensor and N = 76,000 is the number of time samples.
Transfer function for the adaptive optics
The closed-loop transfer curve in Supplementary Fig. 1 reveals 0-dB bandwidths of 110 and 124 Hz for tip-tilt and wavefront correction, respectively. These bandwidths are even slightly higher than when observing granulation with the on-disk AO308 Mk II system of GST.
The transfer function for wavefront mode k was estimated from
$${T}^{\;(k)}(\;f\;)=\frac{{{\rm{PSD}}}_{{\rm{closed}}\,{\rm{loop}}}^{(k)}(\;f\;)}{{{\rm{PSD}}}_{{\rm{open}}\,{\rm{loop}}}^{(k)}(\;f\;)},$$
(5)
where \({{\rm{PSD}}}_{{\text{closed loop}}}^{(k)}(\,f\,)\) is the temporal power spectral density of the root-mean-square wavefront error in the kth mode as reconstructed from the wavefront sensor measurements in the closed control loop. \({{\rm{PSD}}}_{{\text{open loop}}}^{(k)}(\,f\,)\) is the estimated wavefront error before the correction. It was computed from the closed-loop error plus the deformable mirror commands. The commands from two loop cycles earlier were used to account for the latency in the deformable mirror response. The power spectral density was calculated using Welch’s method with a segment length of 1 s, 50% overlap between segments and apodization of each segment with a Hamming window.
Seeing conditions
We estimated the Fried parameter r0 for the seeing in Earth’s atmosphere44 to be of the order of 8 to 14 cm for the dataset used in this performance analysis. This estimate is based on fitting the modal spectrum of the reconstructed wavefront to the spectrum of the theoretical Kolmogorov turbulence. It is difficult to obtain a more precise and accurate estimate of r0 from the available data because the spectra do not fit well. Subjectively, the seeing could be described as ‘normal good seeing’ for the GST.
Hα science observations
The Hα science data were acquired using VIS, which is a single Fabry–Pérot interferometer offering rapidly tunable narrow band-pass imaging. With its telecentric optical configuration, it achieves a spectral band-pass of 0.007 nm for a resolving power of ~105 at 656.3 nm. To maximize the imaging cadence to resolve the rapid dynamics of the upper atmosphere, we elected to operate VIS using a single wavelength sample near the Hα line centre wavelength. The VIS focal plane was recorded using a pco.panda 4.2 bi camera, which yielded a 77% increase of photon collection efficiency compared to the standard VIS configuration. The detector format is 2,048 × 2,048 pix2, and it samples the focal plane with 29 mas per pixel with frame rates up to 40 Hz. At the Hα wavelength, the Nyquist sampling for the 1.6-m telescope aperture was λ/(2D) = 42 mas, and so the VIS oversampled the diffraction limit by ~45%. That is, the theoretical Airy disk was spread over 3 pixels in diameter. For data acquired in 2023, the exposure times were nominally 5 mas acquired at 37 Hz. For data acquired in 2024, a newer version of this camera was installed that offers a low-light mode with reduced dark noise (1.06 e− versus 2.28 e−). We used the low-light mode in all 2024 observations presented here and lowered the exposure time to 1.6 ms to further mitigate the blurring effect of any non-common-path turbulence or vibrations that may or may not exist between the wavefront sensor and the VIS camera. Images were acquired in bursts of 100 frames with variable timing between bursts depending on the expected dynamic in the scenery.
Science image processing and speckle reconstruction
We dark-flat calibrated the raw VIS Hα image bursts and then processed them into an average image using the speckle-imaging KISIP software45, unless noted differently. Speckle imaging mitigates the effect of residual seeing not corrected by the adaptive optics. We used the generic speckle transfer function model built into KISIP instead of a transfer function calibrated for these data, so that the photometric properties of the object may not be accurately reconstructed in the images. In some bursts, the plasma features moved notably between the beginning and the end of the 100-frame burst. We used only 20 frames of each burst for the speckle imaging to avoid smearing effects in the resulting image. Common practice is to use at least 70 frames for good atmospheric statistics. A camera with a higher frame rate could be a future upgrade and would allow us to use more frames for the reconstruction.
Image coalignment and registration
Solar adaptive optic systems are designed to stabilize an image based on a reference feature (a non-point-source ‘guide star’). When that feature moves, the system will attempt to keep it at its original position in the image by driving the field-steering tip-tilt mirror. This effect is amplified in the off-disk case by fast-moving dynamic guide features. To compensate for this effect in the data reported here, we used SDO data at extreme-ultraviolet wavelengths and 160 nm for co-registration. Off-limb, the 160-nm channel was dominated by chromospheric emission46 and most closely matched features observed in Hα.
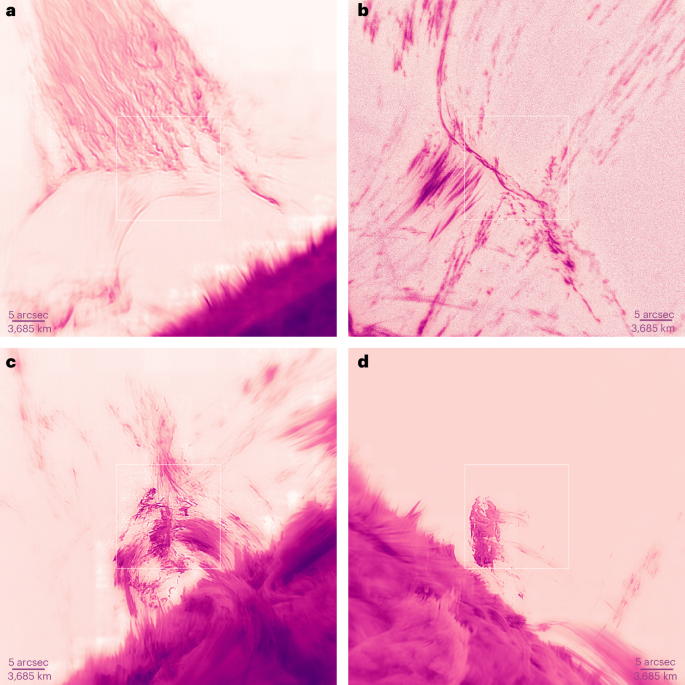
Measuring the widths of coronal rain strands
Semi-automated measurements of coronal rain widths were made by first segmenting the strands and then determining their orientation with the RHT method22. Segmentation involved first creating a high-pass filtered image by dividing the original image by a version convolved with a two-dimensional Gaussian kernel (σ = 3 pixels). The resulting image was then binarized according to a 5% filtered intensity threshold. By using an RHT kernel size of 31 pixels and a threshold RHT resultant length of 0.85, we identified only pixels within the image that have linear coherence in one direction on a length scale of ~0.9 arcsec. This limited the size of structures extracted to those narrower than ~0.3 arcsec. For strands wider than 1 pixel, this process identified several pixels across the structure. To reduce the sampling to 1 pixel along an individual cross section, we found the corresponding pixel in the direction perpendicular to the strand axis that has the largest intensity in the original image. We then performed several Gaussian fits to intensity profiles extracted within ±0.35 arcsec in the direction perpendicular to each strand axis. The minimum intensity was subtracted from the profile to approximate the local background intensity, which includes atmospheric and instrumented scattered light. Each fit used five Gaussian profiles added together. The central Gaussian, which targets the strand being measured, was constrained such that it was separated from the neighbouring Gaussian profiles by at least 5 pixels. The root-mean-square width of the profiles was constrained to be less than 5 pixels. We further required that the derived central position of the strand was within 1 pixel of the maximum intensity of the strand. These safeguards ensured that the central strand was not overfitted by several blended profiles. In total, we extracted the widths of the strands in region 1 (Fig. 4) as fitted from 40,128 individual strand cross sections.