Famously, at the quantum scale, particles can be in multiple possible locations at once. A particle’s state spreads out like a wave, peaking where the particle is likely to be found. When you measure its position, this spread-out state, known as a wave function, transforms into a single definite location.
The full shape of the wave function long evaded detection, since trying to measure it will destroy it. But in the 1980s, physicists began developing methods to measure and control the wave functions of simple systems — advances that have since formed the foundation of quantum computing. And in the last few years, a new approach is enabling physicists to go further and learn about the wave functions of entire materials.
“We are in the second quantum revolution,” said Riccardo Comin, an experimental physicist at the Massachusetts Institute of Technology who is one of the leaders of this work. “Now, we have the tools to really explore the wave function of quantum particles.”
The new framework describes a wave function as an object moving around a hidden landscape — a space referred to as the material’s “quantum geometry.” The hills and valleys of this invisible world dictate how the wave function of a given material can change, and what states the material can be found in.
“You can get a lot of insight into what’s happening in quantum materials, and that may speed up the discovery of new phenomena,” said Marc Bockrath, a physicist at Ohio State University who has also led the charge on quantum geometry.
Comin and collaborators recently measured the full quantum geometry of a crystal — a first peek into the wave function of a real material.
Let’s explore the hidden landscapes that are coming into view.
Secret Geometry
Physicists often think of a particle’s wave function as an arrow. If the particle can be found in two possible states, they represent these options as opposite directions for the arrow to point in — say, up and down. If the particle is in a combination of both states, then the arrow points somewhere around a sphere, with the two states corresponding to the poles.
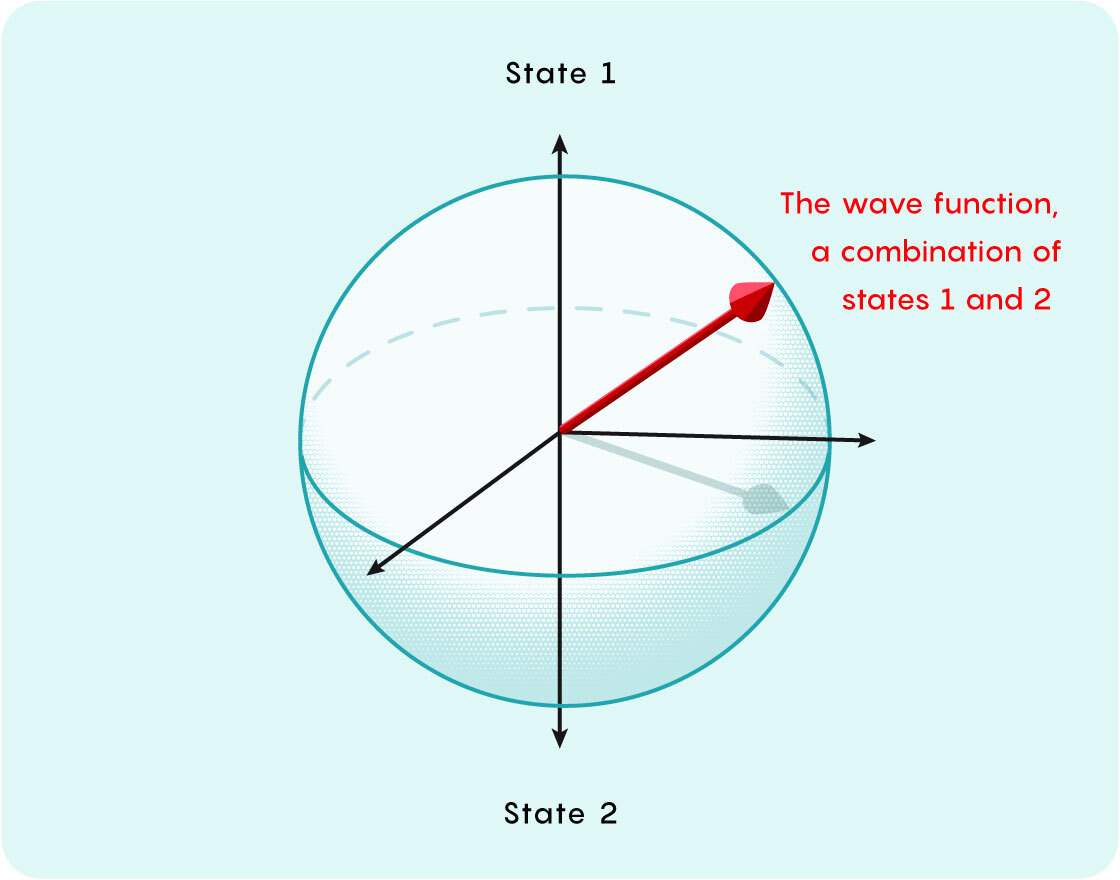
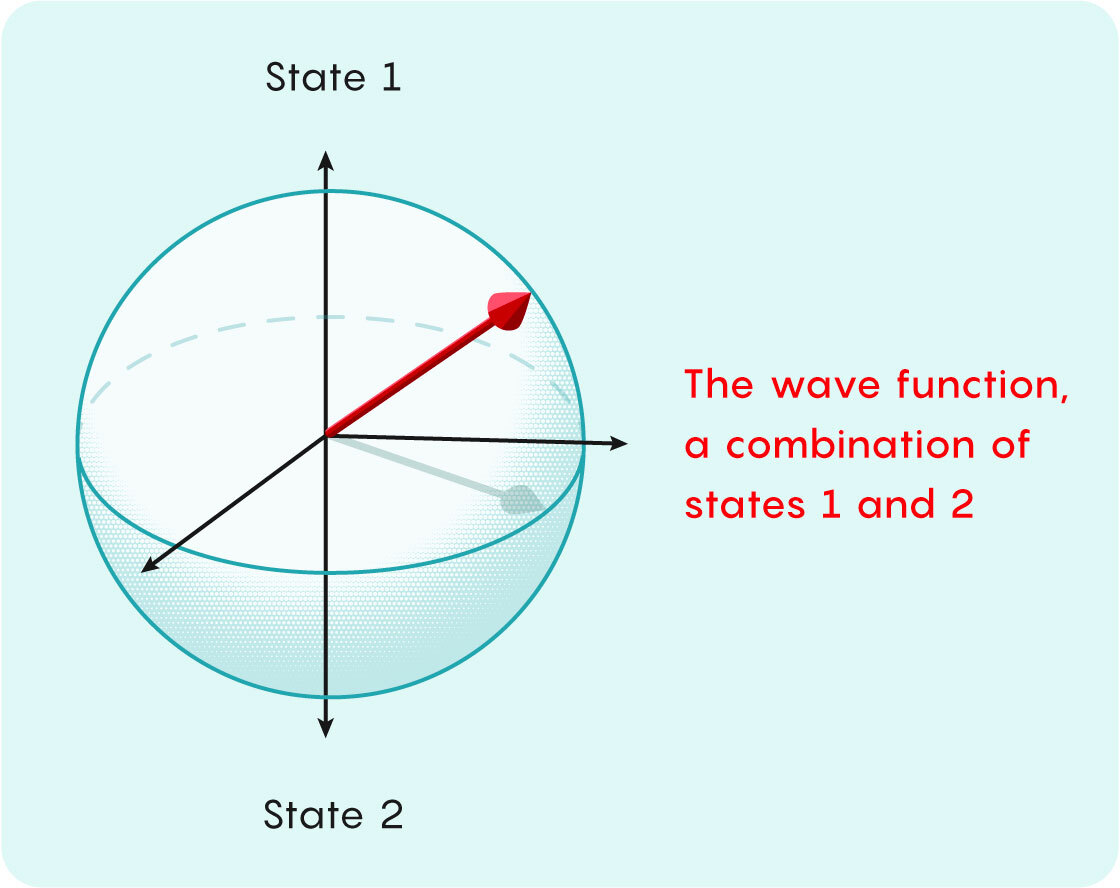
Mark Belan/Quanta Magazine
The arrow’s direction captures the relative likelihood of each possibility. Measuring the particle will snap the arrow into pointing exactly up or down, and the chance of each outcome depends on which pole it’s closest to.
Many particles have more than two possible states, in which case the arrow occupies a high-dimensional space. That’s impossible to visualize, but the math gives physicists a sense of the particle’s wave function at a given moment.
For materials made of many particles, a single high-dimensional arrow can represent the combined state of all the electrons inside it. This collective arrow will swing around as you change the material’s ambient conditions — its temperature, for example, or the strength of the magnetic field around it. To control a material, physicists need to know how the arrow will rotate as they turn these various knobs.
To keep track, they build a map. Imagine, for example, that you change the strength of the magnetic field that you apply to the material. On your map, you’ll make the east-west direction correspond to that magnetic field strength. When the field is weak (corresponding to west on the map), the wave function of your electrons will be in some state, which you can represent with an arrow. With stronger magnetic fields, you’re farther east, and the wave function assumes a different state. As you move from west to east across your map, the arrow will rotate, showing how the wave function of the electrons changes as you dial the field up or down.
