We investigated the nature of mechanical defects in glasses using three distinct 2D model systems. The first two models are glasses: one uses an inverse power-law potential (2DIPL)39,40, which is purely repulsive, and the other employs the classical Kob-Andersen potential (2DKA)41, incorporating long-range attractions. Notably, the results from these models are consistent, with detailed findings from the 2DIPL model presented in the main text and those from the 2DKA model discussed in the Supplementary Information. The third model features a monatomic crystal with point defects, where interparticle interactions are described by the inverse power-law potential. Simulation details are provided in the Methods section.
Characterisation of low-frequency QLMs in glassy solids
We analyse the minimal-frequency vibration modes of the 2DIPL model by diagonalising its Hessian matrix at local minima of the energy landscape. In a large ensemble, most modes exhibit phonon-like characteristics, displaying high participation ratios (PR) and angular frequencies (ω) (see Supplementary Fig. 1). However, some modes show a continuous trend towards lower PR and ω, suggesting the presence of QLMs. This variation across samples raises intriguing questions about the underlying reasons for such differences.
To characterise the vibrational characteristics of QLMs, we decompose the vibrational modes into longitudinal and transverse components in real space using the Voronoi matrix method40,42 (see Methods). In Fig. 1a–c, we illustrate the eigenvector field (u) along with its transverse (uT) and longitudinal (uL) components for a QLM, clearly showing the characteristic four-leaf pattern. The core of QLMs displays randomness in both the direction and length of the vectors, highlighting a significant longitudinal component. This is particularly notable because ω is considerably lower than that of the first longitudinal phonon. Thus, the prominent longitudinal nature of vibrations in the core (Fig. 1c) is a distinctive feature of quadra-polar QLMs.
Fig. 1: Real-space mode decomposition analyses of a typical QLM in 2DIPL.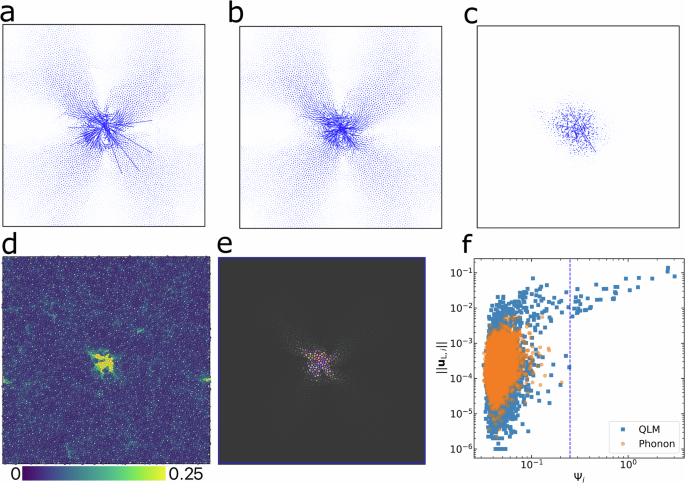
a Full eigenvector field of the QLM (ω = 0.164, PR = 0.005). b Transverse component of the eigenvector field shown in (a). c Longitudinal component of the eigenvector field shown in (a). The magnitudes of the transverse and longitudinal components are 0.865 and 0.135, respectively. The core of the QLM is revealed by the longitudinal component in (c). d Vibrability Ψ field of the QLM, highlighting the core corresponding to (c). e The divergence (\({{\boldsymbol{\nabla }}}\cdot {{{\bf{u}}}}_{i}^{{{\rm{np}}}}\)) field of the net-projection vectors (arrows) of the eigenvector. Blue and red colours indicate regions of negative and positive divergence, respectively, while green represents areas with near-zero divergence. For clarity, only the central region of the QLM is shown, with particle transparency varying according to the magnitude of the vector. f Scatter plot of particle-level vibrability Ψi versus the magnitude of the longitudinal eigenvector ∣∣uL,i∣∣. Data for a phonon mode is also included for comparison. The vertical dashed line indicates Ψi > 0.25.
The cores of low-frequency QLMs have traditionally been identified as regions where the far-field power-law decay of vibrations begins33,36. Here, we characterise the cores of QLMs from a different perspective. To achieve this, we compute each particle’s vibrability Ψi. Vibrability is defined as the susceptibility of particle motion to infinitesimal thermal excitation in the zero-temperature limit37:
$${\Psi }_{i} \equiv {\frac{\partial \left\langle {\left| {{\mathbf{\Delta }}}{{{\bf{r}}}}_{i}\right| }^{2}\right\rangle }{\partial T} \Bigg| }_{T=0}={\sum }_{\lambda=1}^{2N-2}\frac{1}{{\omega }_{\lambda }^{2}}{\left| {{{\bf{u}}}}_{\lambda,i}\right| }^{2},$$
(1)
with Δri = ri(T) − ri(0) denotes the displacement of particle i from its location at T = 0, and ⋅ > represents the thermal average. The second equality holds under the harmonic approximation, with ωl being the eigenfrequency of the lth normal mode, and ul,i the polarisation vector of particle i in this mode.
A higher value of Ψi signifies greater susceptibility to thermal excitation, indicating a more disordered or mechanically soft local environment43. Figure 1d shows the spatial distribution of Ψi, revealing a distinct core that aligns closely with regions exhibiting strong longitudinal vibrational components ∣∣uL,i∣∣ in Fig. 1c. Notably, atoms with high Ψi also exhibit pronounced volumetric deformation, as reflected by elevated values of \({{\boldsymbol{\nabla }}}\cdot {{{\bf{u}}}}_{i}^{{{\rm{np}}}}\) in the divergence field derived from the net-projection of the eigenvectors (Fig. 1e). This volumetric activity stems from the characteristic two-in, two-out vibrations of the key-core structure, which periodically induce the local atomic volume (area in 2D) changes in the surrounding particles (see Methods and Supplementary Fig. 2 for further details).
Although Ψi, ∣∣uL,i∣∣, and \({{\boldsymbol{\nabla }}}\cdot {{{\bf{u}}}}_{i}^{{{\rm{np}}}}\) are derived via distinct methodologies—thermal susceptibility, vibrational mode decomposition and vector field divergence, respectively—their spatial patterns display a notable and visually coherent overlap within the defect core. This convergence, clearly seen in Fig. 1c–e, underscores the robustness of the core’s physical signature across multiple diagnostic lenses. Figure 1f further quantifies this relationship: particles with high Ψi generally exhibit stronger longitudinal displacements ∣∣uL,i∣∣, particularly in the high-Ψ tail. This trend reinforces the use of Ψi as a sensitive and practical indicator for locating the QLM core, characterised by pronounced longitudinal motion. Supplementary Fig. 3 also provides a direct comparison between Ψi and \({{\boldsymbol{\nabla }}}\cdot {{{\bf{u}}}}_{i}^{{{\rm{np}}}}\), revealing that particles with high Ψi frequently coincide with regions of pronounced, non-zero divergence. Notably, \({{\boldsymbol{\nabla }}}\cdot {{{\bf{u}}}}_{i}^{{{\rm{np}}}}\) exhibits both positive and negative values with approximate symmetry, and its spatial distribution appears random—in stark contrast to the crystalline case (see below). This highlights the crucial role of structural disorder in shaping the core structure of QLMs. Furthermore, we confirm that regions with large vibrability (Ψ > 0.25) exhibit a near-zero net divergence on average, indicating that, despite local volumetric fluctuations, the overall volume remains effectively conserved during mechanical deformation.
To assess these correlations more rigorously, we computed the Pearson coefficients between the relevant fields: (1) Ψi vs. ∣∣uL,i∣∣: 0.66 (moderate positive correlation), (2) Ψi vs. \({{\boldsymbol{\nabla }}}\cdot {{{\bf{u}}}}_{i}^{{{\rm{np}}}}\): −0.085 (0.64 when using \(| {{\boldsymbol{\nabla }}}\cdot {{{\bf{u}}}}_{i}^{{{\rm{np}}}}|\)), (3) ∣∣uL,i∣∣ vs. \({{\boldsymbol{\nabla }}}\cdot {{{\bf{u}}}}_{i}^{{{\rm{np}}}}\): -0.207 (0.68 with \(| {{\boldsymbol{\nabla }}}\cdot {{{\bf{u}}}}_{i}^{{{\rm{np}}}}|\)). The low correlation values involving \({{\boldsymbol{\nabla }}}\cdot {{{\bf{u}}}}_{i}^{{{\rm{np}}}}\) underscore that volumetric divergence is not linearly coupled to vibrability or longitudinal displacement —reflecting its nonlinear, possibly threshold-like nature. Nevertheless, the substantially higher correlations observed when using the absolute value of divergence confirm the strong visual alignment of high-intensity regions across the different fields. This convergence indicates that, while the descriptors capture different mechanical aspects, they consistently identify the same localised defect structures, reinforcing the physical coherence of the key-core region from multiple analytical perspectives.
Mechanical excitation of QLMs
To clarify the connection between QLMs and mechanical response44,45,46,46,47, we applied minimal strain deformation to glass samples in an athermal quasistatic manner (see Methods). We then compared the resulting non-affine displacement fields with the eigenvector fields of the corresponding QLMs. In Fig. 2, we show two representative examples of QLMs, each exhibiting distinct spatial orientations.
Fig. 2: Excitation of QLMs through infinitesimal external strain.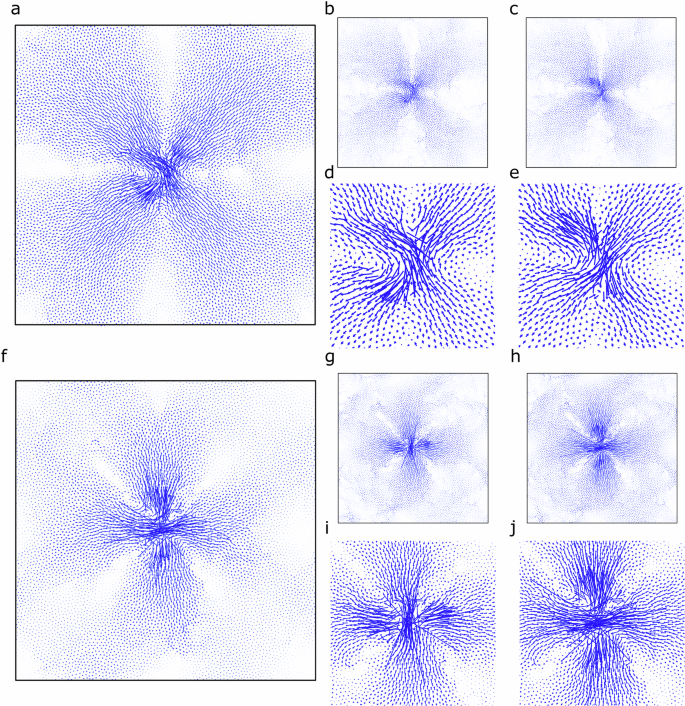
a–e Illustration of a glass sample with a QLM (ω = 0.154, PR = 0.050) oriented close to 45∘. a Eigenvector field of the QLM. b Non-affine displacement field under athermal quasistatic shear deformation along the positive direction of the horizontal axis. d provides an enlarged view of the central region from (b). c Non-affine displacement field under reversed shear direction. e provides an enlarged view of the central region from (c). Note that vector directions in (d, e) are opposite. Importantly, uniaxial tension and compression do not excite this QLM under similar conditions. f–j Illustration of another glass sample with a QLM (ω = 0.150, PR = 0.013) oriented close to 90∘. f Eigenvector field of the QLM. g Non-affine displacement field under athermal quasistatic tension along the horizontal axis. i provides an enlarged view of the central region from (g). h Non-affine displacement field under athermal quasistatic compression along the horizontal axis. j provides an enlarged view of the central region from (h). Note that the vector directions in (i, j) are opposite. We confirm that simple shear cannot excite this QLM under similar conditions.
First, we examine a ‘regular’ four-leaf pattern with an ~45° orientation (see Fig. 2a). We observe that a minimal strain perturbation through simple shear can effectively excite this QLM. The resulting non-affine displacement field closely mirrors the features of the eigenvector field, as shown in Fig. 2b, c. However, the direction of atomic displacement vectors varies depending on the deformation protocol. As highlighted in Fig. 2d, e, non-affine displacements emerge in opposite directions, with the magnitude of vectors differing in each case. This discrepancy likely arises from the orientation-dependent behaviour of shear moduli and the distinct characteristics of the key core structure. Notably, at this minimal strain level, neither tension nor compression effectively excites this QLM. The ~45° oriented QLM is particularly susceptible to shear deformation.
Next, we analyse a four-leaf pattern oriented at nearly 90° (see Fig. 2f). Interestingly, this QLM is easily activated by minimal tension or compression strains but remains unresponsive to simple shear at minimal strain levels. The non-affine displacement fields induced by tension (see Fig. 2g) and compression (see Fig. 2h) closely resemble the pattern observed in Fig. 2f. However, the directions of the displacement vectors in the two protocols are completely opposite, as shown in Fig. 2i, j. The ~90° oriented QLM is particularly susceptible to tension and compression.
Our investigation reveals a notable alignment between the net projection of eigenvectors from neighbouring atoms onto the central atom (see Methods) and the overall eigenvector field pattern. A detailed examination of the divergence field derived from these projections demonstrates that the cores of QLMs display non-zero divergence with approximately balanced positive and negative values, distributed in a seemingly random manner (see Supplementary Fig. 2). This finding supports the presence of disordered volumetric deformation within QLMs, reinforcing their intrinsically amorphous character.
If the four-leaf pattern is oriented between 0° and 90°, excluding 45°, all four deformation protocols can excite the QLM, though with differing intensities. The close spatial correspondence between the non-affine displacement field—arising from each protocol—and the eigenvector field of the QLM strongly supports its mechanical origin. These observations suggest that such QLMs function as dynamical defects, capable of dissipating energy under even minimal strain.
Interestingly, similar protocol-dependent responses have recently been observed in high-entropy alloys, where machine learning techniques were applied to unravel the complex correlations governing their deformation behaviour48. Inspired by this, future efforts could benefit from incorporating data-driven approaches—such as unsupervised learning or graph-based analysis—to systematically identify and classify key-core QLMs across a broader range of glassy systems. These approaches would not only complement physically grounded descriptors but also improve defect detectability in structurally complex or experimentally relevant systems.
These observations highlight the potential for subtle yet irreversible plastic deformation in glassy materials, even under minimal strain. Such deformation can arise while the system remains macroscopically within a nearly linear elastic regime, indicating that QLMs serve as the fundamental units of mechanical instability. These modes may be excited by infinitesimally small perturbations in an amorphous system near marginal stability, where no energy gap exists. This further underscores the inherently inelastic and anharmonic nature of amorphous solids49,50,51,52,53,54.
Our findings support the view that QLMs originate from frustrated local force balances, a phenomenon intimately linked to the form of the interatomic potential. This aligns with recent work (e.g. ref. 55) showing that many-body interactions reduce local confinement, increasing susceptibility to infinitesimal excitations. These insights suggest a deep connection between the microscopic origin of QLMs and the underlying topology of the potential energy landscape, which varies across different interaction models. Investigating how the key-core defects identified in this study evolve under various potentials— especially those incorporating many-body terms—will be crucial for generalising the concept of QLMs across diverse material classes.
The direct correspondence between independent QLMs and non-affine displacement fields elucidates the intrinsic connection between QLMs and shear transformation zones (STZs) in glasses. This assertion is further supported by recent studies that identify QLMs using high-order expansions of potential energy32,33. From a mechanical perspective, distinct cubic modes exhibit four-leaf patterns and are correlated with plastic instabilities, such as local yielding33,56. The spatial orientation of these modes aligns with that of independent QLMs, reinforcing the idea that these four-leaf-type QLMs serve as the origin of soft spots32. Interestingly, cubic modes tend to converge towards QLMs devoid of phonons in the zero-frequency limit. However, the comprehensive isolation of QLMs from strongly hybridised phonons at higher frequencies through cubic modes remains to be confirmed in future research.
Identification of the key core structure of QLMs
Now, we delve into the critical question of what governs the core structure and orientation of these QLMs. One of our key discoveries are visually represented in Fig. 3 through two illustrative examples of glassy samples. First, we focus on atoms with substantial Ψi values (see Fig. 1f). These atoms form the fundamental core of a QLM, as depicted in Fig. 1d, and are further magnified in Fig. 3a1, b1 for two other glasses. This approach enables us to investigate the correlation between the number of particles in the QLM core, denoted as \({N}_{{{\rm{core}}}}\), and its frequency, ω (refer to Fig. 3c). We observe that QLMs with larger cores tend to exhibit lower ω. However, establishing a precise quantitative relationship requires further investigation with more extensive datasets.
Fig. 3: Correlation among vibrability, eigenvector and non-affine displacement fields at the core of QLMs in 2DIPL.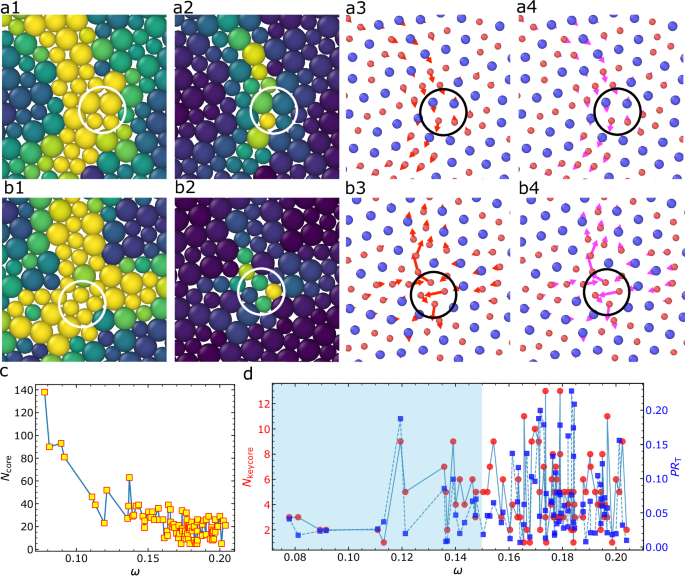
Panels a1–a4, b1–b4 correspond to the QLMs shown in Fig. 2a, f, respectively. The two particle species are distinguished by size. a1, b1 Spatial maps of vibrability Ψi, with high-Ψ atoms (Ψi > 0.25) highlighted in yellow to identify the QLM core (26 and 33 atoms, respectively). a2, b2 Subset of the highest-Ψ atoms (bright yellow), revealing the ‘key-core string’ with a pronounced one-dimensional geometry. a3, b3 Eigenvector fields of the lowest-frequency vibrational modes. Atoms with higher Ψi values show longer vectors aligned along the string-like direction. Full fields are shown in Fig. 2a, f. a4, b4 Non-affine displacement fields induced by minimal strain (simple shear in a4, compression in b4), closely reproducing the eigenvector field patterns. Vector lengths are rescaled for clarity. c Mode frequency (ω) dependence of the number of core atoms (Ψi > 0.25), \({N}_{{{\rm{core}}}}\), sampled over an ensemble of systems. d Frequency dependence of the number of atoms forming the key core, \({N}_{{{\rm{keycore}}}}\) (red circles), and the transverse participation ratio, PRT (blue squares). The shaded region denotes the QLM-dominated regime with minimal phonon coupling.
Interestingly, the core size of an isolated QLM, determined using this method, tends to saturate at approximately 20 atoms as the mode frequency ω increases. This value is consistent with the optimal atom count previously reported for soft spots in binary disordered packings with smaller system sizes20.
Given that our simulation boxes are significantly larger than \({N}_{{{\rm{core}}}}\), and the eigenvector fields associated with QLMs decay rapidly outside the defect core, we conclude that \({N}_{{{\rm{core}}}}\) is not subject to finite-size effects. However, the number of such defects is naturally dependent on system size—larger systems are statistically more likely to host a greater number of independent QLMs, in line with expectations for extensive disordered systems.
It is important to emphasise that, unlike an isolated QLM, a soft spot is defined based on the superposition of multiple low-frequency vibrational modes, and several soft spots can emerge simultaneously20,22,23. While low-frequency phononic modes contribute to soft spots by definition, their influence is limited due to their high participation ratios (PR). These observations suggest that each soft spot fundamentally originates from at least one underlying QLM. The microscopic architecture of soft spots—particularly their connection to specific QLMs—warrants further investigation. Consequently, the total number of soft spots in a glass is expected to scale with the number of QLMs, whether these modes act independently or are hybridised with phonons34. Moreover, our results imply that soft spots associated with particularly low-frequency QLMs may span larger spatial regions and exhibit enhanced susceptibility to external excitation.
In Fig. 3a2, b2, we highlight only the atoms with the highest values of Ψi (see below), revealing a consistent subset of particles that form the ‘key core’ of each QLM. These atoms are arranged in a one-dimensional, string-like configuration, indicative of a vibrational mode that can be excited with minimal volumetric displacement—a characteristic that is particularly favourable in densely packed systems.
Notably, we find no significant correlation between particle species and key-core participation as measured by Ψi. This lack of chemical selectivity suggests that the emergence of key-core defects is dictated predominantly by local mechanical environments, rather than by compositional or species-specific factors.
Examining the eigenvector field in Fig. 3a3, b3, we see that the direction of atomic displacement aligns with the string structure, facilitated by the lack of nearby particles along the vibration direction. Consistent with our earlier discussion, the non-affine displacement field in Fig. 3a4, b4 faithfully reproduces the features of the eigenvector field. This establishes a robust connection between vibrability, eigenvector field characteristics, and plastic deformation.
Notably, despite the string-like structure at the core of a four-leaf-type QLM, its vibrational behaviour is characterised by substantial volume changes. This is evidenced by pronounced longitudinal components in the eigenmode, as shown in Fig. 1c, d. These volumetric vibrations originate from the intrinsic fourfold symmetry formed by four central particles arranged in a square configuration—termed the ‘key-core square’ (see circled regions in Fig. 3a, b). A detailed, quantitative characterisation of the key-core square, including its geometric alignment and two-in, two-out vibrational symmetry, is provided in the Methods section, with illustrative examples presented in Supplementary Fig. 4.
This structure represents the microscopic origin of mechanical frustration within the glass matrix and closely resembles an Eshelby-type inclusion57, which simultaneously produces localised volumetric strain and a long-range shear field. Surrounding the key-core square, a string of particles with elevated vibrability naturally emerges. This string-like vibration arises from nearby particle arrangements that permit low-energy, one-dimensional vibrational motion—especially favourable in densely packed configurations. We refer to this particle string with large vibrability as a ‘key-core string’. The presence of this string serves as both a signature of the defect core and a pathway for mechanical energy localisation. These key-core square and string are embedded within an unstable soft core region characterised by disordered volumetric fluctuations.
To effectively pinpoint the key core string of these QLMs in different glass samples, we come up with a simple empirical criterion: \({\Psi }_{i} > 60\%\cdot {\max }_{i}({\Psi }_{i})\). Although this cutoff is not deterministic—since Ψi is a continuous variable—it effectively isolates the key core, as illustrated in Fig. 3a2, b2. This will be further validated in the following sections.
For samples where QLMs emerge as the lowest-frequency mode in the large ensemble (see Supplementary Fig. 1), we present the size of the key-core strings, denoted as \({N}_{{{\rm{keycore}}}}\), depending on ω, alongside their corresponding transverse part of participation ratio (PRT) in Fig. 3d (see Supplementary Fig. 5 for the total and longitudinal participation ratios). This visual representation vividly captures the synchronised fluctuations of \({N}_{{{\rm{keycore}}}}\) and PRT as a function of ω in the light-blue shaded region, where QLMs is free from coupling to phonons. This revelation adds physical significance to PR, extending beyond its conventional role of distinguishing phonons from QLMs. Furthermore, it underscores the robust localisation of these QLMs, even in the presence of far-field power-law decay features.
We note that Ψ and PRT characterise different but complementary aspects of low-frequency QLMs. The field Ψ quantifies the local vibrational susceptibility, capturing the total amplitude of atomic motion— including both longitudinal (volumetric) and transverse (shear) components—making it particularly effective in identifying the core of soft modes. In contrast, PRT serves as a global metric, indicating the degree of spatial delocalisation specifically associated with the transverse part of a given mode. Figure 3d suggests that QLMs with more extended key-core strings tend to exhibit larger transverse participation, contributing to a higher PRT. This implies that while Ψ highlights local excitability, particularly near the defect core where longitudinal activity dominates, PRT reflects how far the transverse (shear-related) influence of the mode extends across the system. In this sense, the two measures offer complementary insight into the internal structure of QLMs: Ψ resolves the intensity and localisation of excitation, whereas PRT captures the directional extent and delocalisation of transverse response.
Furthermore, as shown in Fig. 1b–d, the transverse component of the eigenmode (Fig. 1b) exhibits a strong spatial resemblance to the Ψ field (Fig. 1d), particularly in the regions beyond the core. Meanwhile, the longitudinal component (Fig. 1c) more clearly reveals the core itself. This visual comparison underscores the hybrid nature of QLMs: they feature both shear-driven and volumetric signatures, with a core dominated by compressive or dilational motion and a surrounding field shaped by long-range shear deformation.
Consequently, a QLM exhibits four distinct structural features: a localised key-core square, a surrounding key-core string, an unstable soft core region characterised by longitudinal vibrational components, and a stable, long-range four-leaf-type shear strain field. The soft core region may correspond to what are commonly referred to as soft spots in disordered solids.
Interestingly, the size of the key-core string, \({N}_{{{\rm{keycore}}}}\), does not directly correlate with the size of the soft core, \({N}_{{{\rm{core}}}}\), as illustrated in Fig. 3c, d. This decoupling suggests that the structural origin of QLMs involves a more complex interplay between localised defects and the surrounding disordered matrix than previously assumed.
While the mechanisms governing \({N}_{{{\rm{core}}}}\) remain somewhat unclear, its variation may reflect the system’s capacity to absorb volumetric deformations within a disordered environment. Specifically, a large value of \({N}_{{{\rm{core}}}}\) implies that the volume fluctuations induced by the two-in, two-out vibration of the key-core square are more effectively accommodated by the surrounding particles. This enhanced ability to accommodate deformation—enabled by local mechanical softness—reduces the mechanical energy cost of excitation, thereby lowering the mode frequency ω, as observed in Fig. 3c.
In contrast, crystalline solids lack this volumetric compensation due to their rigid, ordered structure. As a result, QLMs in crystals exhibit minimal soft core sizes, reinforcing the notion that structural disorder plays a central role in enabling energy localisation and mechanical softness.
These insights underscore the pivotal role of the key-core defect and its immediate environment in shaping the spatial extent and energetic characteristics of QLMs, ultimately defining their function as mechanically relevant excitations in disordered systems.
Finally, motivated by recent developments in the study of topological defects in disordered systems26,27,28, we perform a topological characterisation of the eigenmodes shown in Fig. 2a, f. The analysis follows established procedures, with full methodological details provided in Supplementary Note 1. In addition to the full eigenmodes, we also apply the same analysis separately to their transverse and longitudinal components. Interestingly, in both cases, a persistent negative topological defect consistently appears at the centre of the four-leaf pattern, aligning with the core region of the QLM. However, numerous additional topological defects are detected in peripheral regions where vibrational amplitudes are negligible (see Supplementary Fig. 6). Notably, the longitudinal component—despite having much smaller overall amplitude than the transverse part—exhibits a larger number of topological defects. This discrepancy arises because the definition of topological defects relies solely on the orientation of eigenvectors—regardless of their magnitude. These observations suggest only a partial spatial overlap between topological defects and the mechanically defined key-core defects identified in this work. This distinction may help explain the absence of a strict one-to-one correspondence between topological defects and plastic events, as reported in prior studies26.
Shear anisotropy induced by hierarchical defects
We now aim to establish a link between the identified localised defects and the mechanical properties. The dominant role of the transverse component in the eigenmode suggests a significant role of the shear modulus associated with the QLMs. A QLM can lead to shear anisotropy and softening. Therefore, we focus on the simple shear modulus G.
Due to the spatial variation in the orientation of QLMs, as demonstrated above, relying solely on the horizontal direction of shear deformation may not adequately capture shear modulus anisotropy. To address this, we measure the orientation-dependent shear modulus G(θ) using the approach introduced in ref. 58. Here, θ denotes the clockwise rotation angle of the sample’s horizontal axis relative to its original orientation.
We identified two typical cases in glassy solids, as illustrated in Figs. 4,, 5. These examples correspond to the cases discussed earlier in Figs. 2, 3. Additional examples are shown in Supplementary Figs. 7, 8.
Fig. 4: Shear anisotropy induced by hierarchical QLMs.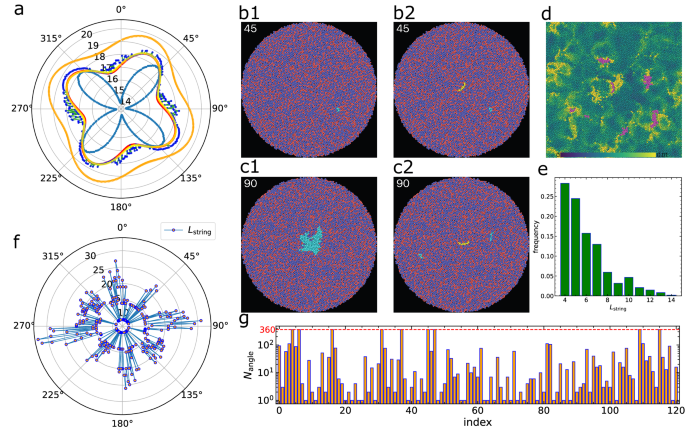
a Angular dependence of the simple shear modulus G(θ) in polar coordinates for the system shown in Fig. 2a. Five measurements are shown, from inner to outer: (light blue) unpinned system; (red) with key-core string atoms pinned (yellow atoms in b2); (yellow, nearly overlapped with red) with only key-core square atoms pinned; (blue) with both key-core atoms and θ-dependent strings pinned (yellow and cyan atoms in c2, θ = 90∘); (orange) with key-core atoms and all hidden strings pinned (magenta atoms in d). b1, c1 Excited atoms (cyan) with large non-affine displacements at θ = 45∘ (b1) and 90∘ (c1) when no pinning is applied. b2, c2 Same configurations after pinning the key-core atoms (yellow), showing suppression of the primary QLM at θ = 90∘ (c2) but not at θ = 45∘ (b2). d Spatial distribution of reduced transverse vibrational density of states, \({D}_{i}^{{{\rm{T}}}}(\omega )/\omega\) for ω = 0.8 ± 0.4. Magenta atoms represent the union of the key-core and θ-dependent string excitations. e Length distribution of θ-dependent strings with Lstrings > 3, showing a rapid decay in string length. f Angular dependence of the number of atoms participating in the key-core and hidden strings. This curve maps closely onto the anisotropy observed in G(θ) (compare with blue curve in a). g Frequency of pinning occurrences for each magenta atom from (d), as the system is rotated in 1∘ increments over 360∘. Atoms with Nangle = 360 (horizontal red dashed line) are the key-core atoms that are always excited. Other atoms show orientation-specific excitation, confirming the directional nature of string-like defects.
In general, G(θ) exhibits substantial angular dependency, which varies among different samples. By comparing the eigenvector field of the QLM with G(θ), we observe that the reduction in G(θ) towards the weakest orientation and the rate of decline are influenced by the characteristics of the QLMs. Notably, the smallest G(θ) corresponds to the minimal phonon velocity, and this orientation-dependent phonon velocity can render the separation of QLMs from phonons, based on phonon velocities estimated from macroscopic shear modulus measurements, unreliable.
Figure 4 illustrates the microscopic features corresponding to the QLM in Fig. 2a. Significant shear softening and shear anisotropy are evident from G(θ), as shown in Fig. 4a (inside light-blue curve). This anisotropic response to mechanical stimuli has been experimentally observed in metallic glasses54.
We present the excited atoms (cyan) with large non-affine displacements in the strongest direction (~45°) and the weakest direction (~90°) in Fig. 4b1, c1, respectively. At θ = 45°, the QLM is not excited, and only a minor secondary string is activated (cyan particles in Fig. 4b1). In contrast, at θ = 90°, the QLM is significantly excited, with no other strings activated, as shown in Fig. 4c1. This observation explains the shear softening observed in different directions. By pinning the key-core string atoms of the QLM (yellow atoms in Fig. 4b2, c2), we find that the excited atoms at θ = 45° remain largely unchanged (compare Fig. 4b2 with Fig. 4b1). In contrast, pinning at θ = 90° fully suppresses the non-affine deformation from the QLM, with only minor secondary strings (cyan particles in Fig. 4c2) taking up the shear strain. The full non-affine displacement fields are shown in Supplementary Fig. 9 (see Supplementary Movies S1,S2 illustrating the orientation-dependent excitation of the QLM in glasses with and without atomic pinning, respectively).
When we measure G(θ) with the key-core string or key-core square atoms pinned, the shear softening and shear anisotropy are greatly reduced, as seen from the red or yellow curves in Fig. 4a, respectively. A closer examination reveals that pinning a key-core square is slightly more effective in reducing these effects, highlighting its critical importance. This outcome is expected, as only the key-core square exhibits two-in, two-out vibrations, which are responsible for the fourfold symmetry. The key-core string arises as a consequence of the key-core square and reflects the preference for one-dimensional vibrational excitations.
During shear deformation under atomic pinning, significant non-affine displacements are realised by string-like atom chains, such as those shown in Fig. 4c2. These secondary strings have much higher activation energy than the primary QLM at the centre and can be selectively excited depending on θ. We visualise all the excited strings at 0°–360°, including the key core string, as magenta particles in Fig. 4d. Despite their excitation at different angles, these strings largely overlap spatially (see Supplementary Movies S1, S2), obscuring their string-like feature in Fig. 4d. This suggests the existence of hidden defects that depend on the system’s structure and may vary with different glass states. Interestingly, Fig. 4d shows that these magenta atoms nearly overlap with the atoms exhibiting a large reduced transverse density of states at low frequencies, below the boson peak40.
Additional analyses of these hidden strings reveal the length distribution of strings with more than 3 particles, as shown in Fig. 4e. The data indicate a rapid decay in the number of strings as their length increases, suggesting that shorter strings are generally more prevalent, especially among those that can be excited by minimal strain. This trend is intuitive, as longer strings require more specific particle arrangements to support one-dimensional particle motion. The angular (θ-) dependence of the number of particles in a string, Lstring, for all strings in the system, as shown in Fig. 4f, closely mirrors the shape of G(θ) measured without atomic pinning.
In general, higher rigidity in a solid corresponds to a lower density of defects. The angular distribution of defect-associated atoms shows clear peaks near θ = 0°, 90°, 180° and 270°—precisely the directions where G(θ) exhibits the most pronounced softening in the unpinned system. This alignment supports the view that directional excitation of string-like defects plays a key role in mechanical softening. The observed correlation between Lstring(θ) and G(θ) thus reinforces our claim that the anisotropic mechanical response is rooted in the θ-dependent activation of these defects. This similarity further indicates that these hidden secondary string-like defects, together with the key-core square and string structures, significantly contribute to shear softening.
Repeating the atomic pinning process by also pinning particles in the angle-dependent string at each θ (Fig. 4f), we measure a new G(θ), depicted by the blue dot in Fig. 4a. This operation (blue dots) reduces shear anisotropy but remains comparable to the red curve. On the other hand, pinning all magenta particles in Fig. 4d and measuring G(θ) results in the outer orange curve in Fig. 4a, showing a significant reduction in shear anisotropy. The remaining anisotropy may be due to defects undetected with the cutoff in the non-affine displacements, i.e. weaker contributors not included in the analysis. We propose that the hierarchical nature of defects in glasses, which display continuous variations in activation energies and strain responses, arises as a consequence of the underlying structural disorder.
From all strings in the system, including both the key core and hidden defects, totalling 121 particles (visualised in Fig. 4d), we plot the number of times these atoms are pinned at different θ values (with a 1° step) in Fig. 4g. For instance, the key core atoms are consistently pinned, resulting in a value of 360. Atoms are pinned at each θ only when they are excited, without pinning, excluding the key core atoms, which are always pinned. Thus, pinning times inherently reflect excitation times. Many of these particles are excited at multiple angles, reflecting various string forms, further demonstrating the orientation sensitivity of string-like defect excitations in glasses, as highlighted by the curved arrangement of the key core atoms. This multiple excitability of string-like particles across different orientations explains why pinning them at a single angle does not substantially reduce the anisotropy in G(θ) (blue dots in Fig. 4a), when compared to the yellow and red curves.
Considering the association between four-leaf QLMs and soft spots, the orientation-dependent behaviour of QLMs—and consequently the shear modulus—naturally explains why not all soft spots are activated within a single plastic event. This anisotropy in soft spots highlights their diverse activation conditions, providing a valuable perspective for future research. Understanding this phenomenon could offer deeper insights into the mechanics of glassy materials and the nature of plastic deformation.
We now turn to the other typical case illustrated in Fig. 5, corresponding to the QLM in Fig. 2f. The shear softening and shear anisotropy observed from G(θ), represented by the inner light-blue curve in Fig. 5a, are pronounced, similar to the previous case, but in different directions from the one in Fig. 4a. As before, we examine the non-affine displacement fields under minimal shear deformation along the weakest (θ = 45°) and strongest (θ = 90°) directions, shown in Fig. 5c1, d1, respectively. Consistently, at θ = 45°, the QLM is prominently excited, exhibiting a four-leaf pattern with no other atoms activated. Conversely, at θ = 90°, the QLM is significantly suppressed, and a hidden secondary string is activated.
Fig. 5: Shear anisotropy induced by a primary QLM.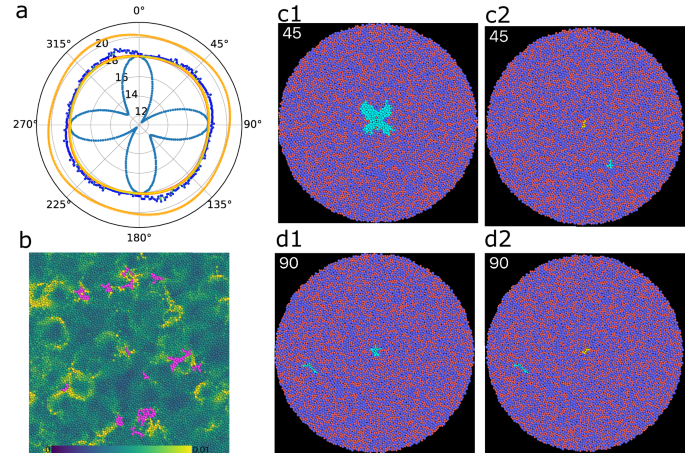
a G(θ) in polar coordinates for the system in Fig. 2f. The colour scheme in (a) and the atomic colouring strategy in other panels are consistent with those in Fig. 4. b Particle-level reduced transverse density of states, \({D}_{i}^{{{\rm{T}}}}(\omega )/\omega\), for ω = 0.8 ± 0.4. The magenta atoms represent the union of θ − dependent strings and the key core atoms. c Atomic configurations at θ = 45∘ with excited atoms marked as cyan when the key core atoms unpinned (c1) or pinned (yellow atoms) (c2). d Atomic configurations at θ = 90∘ similar to (c) when the key core atoms unpinned (d1) or pinned (d2).
After pinning the key-core string (the yellow atoms in Fig. 5c2, d2), the QLM is completely suppressed, with only secondary strings remaining active. The full non-affine displacement fields for Fig. 5c1, c2, d1, d2 are presented in Supplementary Fig. 9.
More significantly, when examining G(θ) in Fig. 5a after pinning only the key-core square atoms composed of four atoms (circled atoms in Fig. 3b) or the key-core string particles, the shear anisotropy almost disappears (nearly overlapping yellow and red curves, respectively), rendering the system nearly isotropic—distinct from the previous case. We also extract all hidden strings and display them collectively in Fig. 5b as magenta particles. Pinning the angle-dependent strings in addition to the key-core atoms, individually or together, results in only a slight reduction in shear anisotropy, as indicated by the blue dots and orange curves in Fig. 5a. However, the amplitude of the shear modulus is increased when all particles are pinned.
We speculate that the significant difference from the case in Fig. 4 may be due to the substantially higher activation energy of the hidden strings compared to the key core ones in this case. Consequently, these hidden strings contribute less to shear instability at minimal strain. This variation underscores the inherent disordered structure of glasses, which creates a diverse distribution of local states with varying activation energies, leading to hierarchical defects. This implies that such defects are likely influenced by the thermal history of the sample.
Here, we note that these observations are also common to another system we studied, namely the 2DKA model. Representative results are presented in Supplementary Figs. 10,11, demonstrating the broad applicability of our findings to systems with both repulsive and attractive interactions.
These observations highlight the critical role of the key-core square and string atoms at the centre of the most prominent QLM in determining both the four-leaf anisotropy of the QLM and the shear anisotropy. The highly localised nature of these key-core squares justifies their classification as ‘defects in a glass’. Higher-order defects, composed of many hidden strings, have a minor yet non-negligible impact on the system’s mechanical properties. The hierarchical nature of defects in glasses, stemming from underlying structural disorder, distinguishes them from defects in crystals (see below).
The results not only reinforce our assertion that the key-core square of the four-leaf-pattern QLMs acts as mechanical defects in glasses but also provide further evidence for the existence of soft spots potentially involving multiple QLMs. It is notable that the mechanical coupling of multiple QLMs could give rise to intriguing memory effects, as discussed in previous studies59. Additionally, the observed pinning effect highlights the crucial role of the string-like vibration’s orientation in shaping the spatial characteristics of the four-leaf pattern. Further investigation is needed to explore the underlying physical mechanisms behind these phenomena.
Shear anisotropy triggered by QLMs in a defected crystal
The mechanical defect-like nature of the QLM’s key core suggests that QLMs are not exclusive to glassy materials and could potentially exist in any system where space permits transverse motion, aligning with examples observed in crystals38. To investigate how structural disorder affects the occurrence of low-frequency QLMs, we performed simulations on a monatomic crystal with inherent point defects like vacancies (see Methods). This crystal, formed through slow cooling, demonstrates hexatic order with quasi-long-range positional and long-range orientational orders.
In the defected crystal with two vacancies, we begin by analysing the minimal-frequency vibration mode and decompose it into transverse and longitudinal components, following the same method used for glasses. Remarkably, the phononic mode is intricately coupled with two QLMs that exhibit characteristic four-leaf patterns. These QLMs are centred around the vacancies, setting them apart from soft spots in imperfect colloidal crystals, which do not effectively detect vacancies25. Figure 6a illustrates the transverse component, while the full eigenvector field and the longitudinal component can be found in Supplementary Fig. 12. Similar to the behaviour observed in glasses, the predominant component of the mode is transverse, though the longitudinal component is also significant. Notably, atoms participating in the four-leaf pattern consistently show more pronounced longitudinal components.
Fig. 6: Vibration modes and the associated shear anisotropy of a monatomic crystal model with defects.
a The transverse component of the minimal-frequency vibration mode, with an amplitude of 0.968. b Visualisation of the atomic-scale vibrability Ψi. The two vacancy defects are indicated by the four red particles. c G(θ) of the defected crystal in polar coordinates. The inner blue curve illustrates G(θ) in the normal (unpinned) state, while the outer red curve shows G(θ) with the four key core atoms (see b) pinned. d The divergence (\({{\boldsymbol{\nabla }}}\cdot {{{\bf{u}}}}_{i}^{{{\rm{np}}}}\)) field of the net-projection vectors (arrows) of the eigenvector. The QLMs have been shifted to the centre for better visualisation. Blue and red indicate negative and positive divergence, respectively, while green represents nearly zero divergence. The divergence patterns resemble intricate butterfly shapes. Panels (e, f) provide enlarged views of the left and right QLMs in (d), respectively. The yellow atoms at the centre are the key core atoms, corresponding to the red ones in (b).
Simultaneously, the four-leaf pattern feature aligns well with the atomic-scale vibrability Ψi (see Fig. 6b and Supplementary Fig. 12). This highlights Ψ’s effectiveness in identifying crystal defects, just as in amorphous systems.
To investigate the mechanical properties of QLMs in a manner similar to our glass studies, we apply four distinct deformation protocols to excite them. Due to the specific orientation of the QLMs, all four deformation methods can activate them, albeit to different degrees (see Supplementary Fig. 12d1–d4). The resulting non-affine displacement fields consistently reflect the characteristics of the QLMs observed in the eigenvector field.
We further perform an eigenvector projection analysis (see Methods), specifically targeting the QLMs. The resulting projection product accurately captures the vector characteristics, with its divergence field showing non-zero values at the QLM cores (see Fig. 6d–f). Interestingly, the regions surrounding the vacancy display either positive or negative divergence, indicating the presence of volumetric deformations.
Notably, the atoms with the largest Ψi values, especially around the vacancy, define the location of the QLMs, displaying a gradient with a string-like feature. This observation is consistent for both QLMs, as illustrated in the enlarged views in Supplementary Fig. 13a, d. The eigenvector direction of the QLM aligns consistently with this string structure (see Supplementary Fig. 13b, e). Remarkably, the non-affine displacement fields from all deformation protocols exhibit features similar to those of the eigenvector field. As observed in glasses, the vector directions are opposite between the simple shear and between tension and compression (see Supplementary Fig. 13c, f).
Adopting a methodology similar to that used for glasses, we focused on four key core atoms within the crystal (red particles in Fig. 6b) and investigated their impact on mechanical properties using atomic pinning. First, we analysed G(θ) in the unpinned original system (see Fig. 6c). This analysis reveals a significant and pronounced anisotropy, with the direction of the weakest shear modulus, G(θ), determined by the orientation of the QLM’s key core, while the remaining atoms are positioned within the perfect lattice. Pinning these four key core particles reduces the observed anisotropy in G(θ) to nearly negligible levels, resulting in a significantly stiffer and more isotropic matrix (see Supplementary Movies S3, S4 for the orientation-dependent non-affine displacement field).
The findings from the defective crystal studies indeed reinforce the view that QLMs are fundamental dynamical defects across different material types. Their behaviour as force dipoles and the consistent presence of key-core squares and strings highlight their significant role in both crystalline and amorphous materials. This broadens our understanding of how such defects influence mechanical properties and highlights their relevance for various applications and material designs.