Understanding and controlling electron dynamics at ultrafast timescales is a cornerstone of modern photonics and quantum control. Photoionization at energies lying between the numerous ionization thresholds of multi-electron systems invariably leads to the creation of a doubly excited electron wave packet (EWP) embedded in an electronic continuum. Owing to electron–electron interactions, the EWP decays through autoionization to the continuum, and this continuum wave packet interferes with the original EWP, giving rise to quantum-path interference. This autoionizing process was explained and formulated by Fano1,2. It can describe many resonance phenomena in diverse settings, ranging from nuclear3 to atomic4,5,6,7 and molecular8 scale to condensed-matter physics9, single-molecular functional devices10 and nanostructures11,12,13,14,15. Depending on the strength of the electron interactions, the natural lifetime of a Fano resonance ranges from nanoseconds to femtoseconds. The dynamical evolution of Fano resonances has been theoretically investigated16,17,18,19,20 and experimentally realized in different set-ups4,5,21,22,23,24,25,26. By using an intense near-infrared (NIR) laser field (~1013 W cm−2), one can terminate the exponential decay at a given time and observe the build-up of the Fano profile through absorption measurements4,27. The NIR pulse can also be used to control the phase difference between the resonant and continuum transition channels28 and the lifetime of the Fano resonance29. Alternatively, the so-called ‘rainbow’ reconstruction of attosecond beating by interference of two-photon transitions (RABBIT) technique5 has been used to determine the dynamics of Fano resonances by reconstructing resonant EWPs through photoelectron interferometry.
To deepen our understanding of these dynamics, it is essential to fully characterize the quantum properties of resonant EWPs, including both the amplitude and phase. These quantum properties are also key to advance the coherent manipulation of the wavefunction of electrons, thereby extending the potential applications of free-electron-based technologies in electron beam lithography30,31, ultrafast electron microscopy32,33,34,35,36,37 and ultrafast transmission electron microscopy38,39,40. The considerable expectations for these technologies call for a means to both measure and characterize the free-electron quantum states. Such a technique could parallel the advances made by a similar development for light pulses: frequency-resolved optical gating (FROG)41,42,43,44 now serves as a universal diagnostic tool that provides amplitude and phase information for ultrashort chirped laser pulses.
In this study we introduce and demonstrate a framework for the creation, measurement and full characterization of coherent EWPs. To provide a specific example, we focus on EWPs launched in the vicinity of the He(\({{{sp}}}_{2,3}^{+}\)) (63.66 eV) doubly excited state using various engineered extreme ultraviolet (XUV) excitation pulses. With an additional weak NIR field (800 nm, ~1010 W cm−2) acting at a given XUV-pump, NIR-probe time delay, the resonant EWP is instantaneously mapped to time-resolved photoelectron spectra via the absorption of one NIR photon. This laser-assisted photoelectric effect45,46 takes advantage of a perturbative treatment, enabling us to fully reconstruct the field-free intrinsic EWP, as well as completely follow its dynamical evolution from birth to the end of its lifetime (\({\sim}79.{3}_{-4.5}^{+5.1}\,{\rm{fs}}\))47,48. We have also developed a reconstruction method based on a short-time Fourier transformation to retrieve the temporal profiles of the EWPs.
This method is directly applicable to any other quantum system, provided that the individual final quantum states of the ionized system can be resolved. The ability to access both the amplitude and phase of EWPs provides a new perspective on quantum interference and coherence in ultrafast processes. Beyond our immediate findings, this approach offers a broadly applicable methodology for the study of core-excited states and shape resonances. We predict that this methodology can be extended to nuclear degrees of freedom, including Feshbach resonances in polar molecules. Such advancements expand the toolkit for probing and manipulating quantum systems across diverse fields, from atomic and molecular physics to condensed matter and nanophotonics.
The standard Fano resonance is illustrated in Fig. 1a. Close to the doubly excited state (\({{sp}}_{2,3}^{+}\)), we photoionize helium with an XUV pulse obtained through high-harmonic generation from gaseous neon, leading to the emission of a resonant EWP with a complex spectral amplitude and phase. The spectral amplitude can be directly measured by a photoelectron spectrometer. However, the EWP phase is not accessible with static measurements, similarly to spectral measurements of optical pulses. Dressing with a weak NIR field partly gates the evolving resonant EWP in the time domain through the absorption of a single NIR photon. This manifests in the energy domain as a sideband, the energy of which is blueshifted from resonance by one NIR photon energy (Fig. 1b). Therefore, the full shape of the resonant EWP can be sampled by varying the time delay between the XUV pump and NIR probe pulses, and can be resolved in the frequency domain. Our framework makes use of a principle similar to that of FROG (Fig. 1c), where a laser pulse that is to be characterized is gated with a delay function and resolved by an optical spectrometer. By scanning the time delay between the laser pulse and the gate, both the amplitude and phase of the laser pulse can be retrieved accurately.
Fig. 1: Principle and experimental demonstration of photoelectron FROG.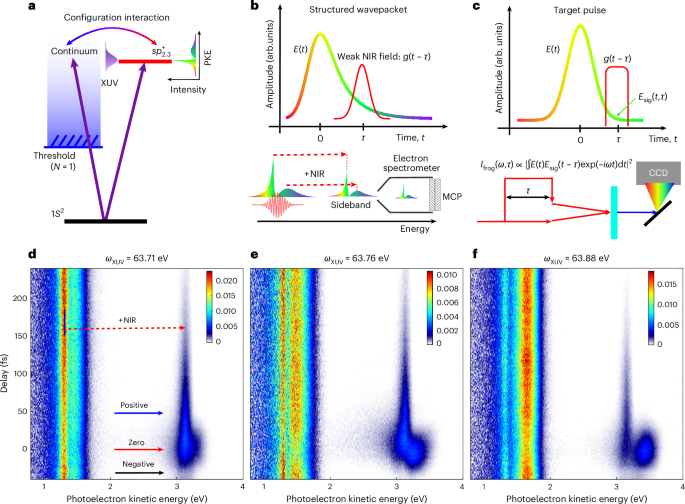
a, Schematic diagram of a standard Fano resonance in the vicinity of He(\({{{sp}}}_{2,3}^{+}\)) at the resonant energy 63.66 eV. The resonant EWP is created by a blueshifted XUV pulse, the pathway interference leads to a dual-peak distribution of the static photoelectron spectrum. b, Principle of photoelectron FROG. In the presence of a weak NIR field, the evolving EWP is partly gated by the absorption of a single NIR photon in the time domain, leading to the depletion of the main peak and formation of a sideband in the frequency domain, which are both recorded by a photoelectron spectrometer. c, Principle of FROG. The target laser pulse (E(t)) is gated by a variable-delay function (g(t − τ), where τ is the lifetime), leading to replicas of itself in an instantaneous nonlinear optical medium, which are recorded by an optical spectrometer (CCD, charge-coupled device). d, Time-resolved photoelectron spectrum measured with a photon energy (ωXUV) of 63.71 eV. The red dashed arrow represents one NIR photon absorption. Blue arrow indicates photoelectron signals measured at positive pump-probe delays; red solid arrow corresponds to photoelectron signals taken around time-zero; black arrow indicates the photoelectron signals were measured at negative pump-probe delays. e,f, The same as d but with XUV energies of 63.76 eV (e) and 63.88 eV (f), respectively. The delay between the XUV and NIR pulses was scanned in steps of 2 fs from −60 fs to +240 fs, where a positive delay indicates that the XUV pulse precedes the NIR pulse. A negative bias potential (−38 V) was applied on the photoelectron spectrometer to achieve a spectrally resolved measurement (see the Methods for details). The colour scales in d–f refer to the photoelectron signal in arbitrary units (arb). PKE, photoelectron kinetic energy; MCP, microchannel plate detector; Ifrog, intensity of the FROG signal; Esig, electric field of the gating pulse; units, arbitrary units.
Measured time-resolved photoelectron spectra with different XUV central energies are shown in Fig. 1d–f. The high energy resolution (~0.1 eV) was achieved by imposing an optimized negative bias potential on the spectrometer to decelerate the photoelectrons. In the absence of the weak NIR field, the ionized EWP displays two peaks: a sharp peak at low photoelectron energies and a broader peak at higher energies. These two features verify the formation of a structured EWP through XUV ionization, with the sharp peak representing the resonant component and the broader peak the continuum component (Fig. 1a). Taking the phase-matching condition in high-harmonic generation into account, the XUV-pump pulse (of harmonic order H41) was optimized by a blueshift, resulting in a central energy that was higher than the \({{sp}}_{2,3}^{+}\) resonant energy (63.66 eV). The absorption of this engineered XUV photon leads to the simultaneous creation of a doubly excited autoionizing state and direct ionization to the continuum, typically manifesting as a Fano resonance. As the central XUV energy increases (Fig. 1d,e), direct excitation of the continuum component increases, resulting in an enhancement of the broad distribution at higher electron energies. Interestingly, despite the increase in the central XUV energy, the position and width of the sharp peak remained unchanged, reflecting the contribution of the resonant component. In the presence of a weak NIR field, the resonant EWP is blueshifted by the absorption of one NIR photon49,50 and exhibited distinct dynamical structures, particularly when the XUV and NIR pulses overlapped.
To interpret our time-resolved data, we theoretically benchmarked the two-photon transition of helium in the vicinity of the \({{sp}}_{2,3}^{+}\) resonance. The transition amplitude from the initial (ground) state |g〉 to the final (continuum) state |E〉 through the absorption of two photons from the light fields F1(t) and F2(t) sequentially is given by:
$$\begin{array}{l}{M}_{E}=\mathop{\int}\nolimits_{\!-\infty }^{\infty }{\rm{d}}t\,{F}_{2}(t){{\rm{e}}}^{{{\mathrm{i}}Et}}\mathop{\int}\nolimits_{-\infty }^{t}{\rm{d}}{t}^{{\prime} }\,G(t-{t}^{{\prime} }){F}_{1}({t}^{{\prime} }){{\rm{e}}}^{-{\rm{i}}{E}_{g}{t}^{{\prime} }}\\\qquad\equiv \mathop{\int}\nolimits_{\!-\infty }^{\infty }{\rm{d}}t\,{F}_{2}(t){{\rm{e}}}^{{{\mathrm{i}}Et}}P(t),\end{array}$$
(1)
where G(τ) is the time-domain Green’s function (see Supplementary Note 2 for details). The gating mechanism in this two-photon absorption process becomes obvious when the EWP, created by photoabsorption from the first pulse F1(t), is denoted P(t), where t is the time elapsed since the resonance was populated. Then, ME is a short-time Fourier transformation of P(t) with the window function F2(t).
Hence, by measuring the photoelectron energy distribution ∣ME∣2 at different energies and time delays (that is, by varying the window function position), one can in principle directly reconstruct the full information of P(t), except for an unimportant global phase. In our experimental configuration, the structured EWP is energetically close to a doubly excited state that can be parameterized as a Fano resonance, with resonant energy Er, lifetime 1/Γ and Fano asymmetry parameter q. Therefore, G(τ) can be written as:
$$G(\tau )\propto -r{\rm{i}}\varGamma /2(q-{\rm{i}}){{\rm{e}}}^{-{\rm{i}}{E}_{\mathrm{r}}\tau -\varGamma \tau /2}\varTheta (\tau )+\updelta (\tau ),$$
(2)
where r is a dimensionless parameter close to 1 and the exponential decay represents the transition where the electron stays in a doubly excited state for a time τ before absorbing the second photon. The Dirac-δ(τ) function represents the direct transition to the continuum, where the electron absorbs two photons simultaneously. If the pump-pulse duration of F1(t) is short enough and r = 1, we obtain the exact windowed-Fourier transformation of a Fano resonance.
In Fig. 2, we demonstrate the evolution of a prototypical Fano resonance with an energy width of 8.3 meV gated by an IR pulse with an energy width of 35 meV at different time delays. For a negative delay (Fig. 2a), the population of the excited state is only slightly influenced by the IR pulse, meaning that direct two-photon transitions to the continuum dominate. Consequently, the narrow peak in the time domain gives rise to a single peak with a broad distribution in the energy domain. For positive delays (Fig. 2c), the continuum part of the EWP is poorly populated, while the exponential decay tail of the resonant component interacting with the NIR pulse produces a relatively broad peak in the time domain, resulting in a narrow single peak in the energy domain. For time delays approximately equal to zero (Fig. 2b), the continuum component and the resonant component are roughly equally populated. One can see that destructive interference converts the gated photoelectron spectrum for negative time delays to one with a dip at the position of the resonance (right column). A comparison with the experimental results (Fig. 1d–f) shows that most of the characteristics of the experimental sideband are captured by our theoretical predictions. For a negative time delay, the experimental sideband exhibits a broad distribution for all three XUV energies. During the cross-correlation, a distinct double-peak structure is observed, and the relative ratio between these two components is correlated with its main peak. For positive time delays, a single sharp peak remains, as the continuum component has vanished.
Fig. 2: Illustration of photoelectron FROG.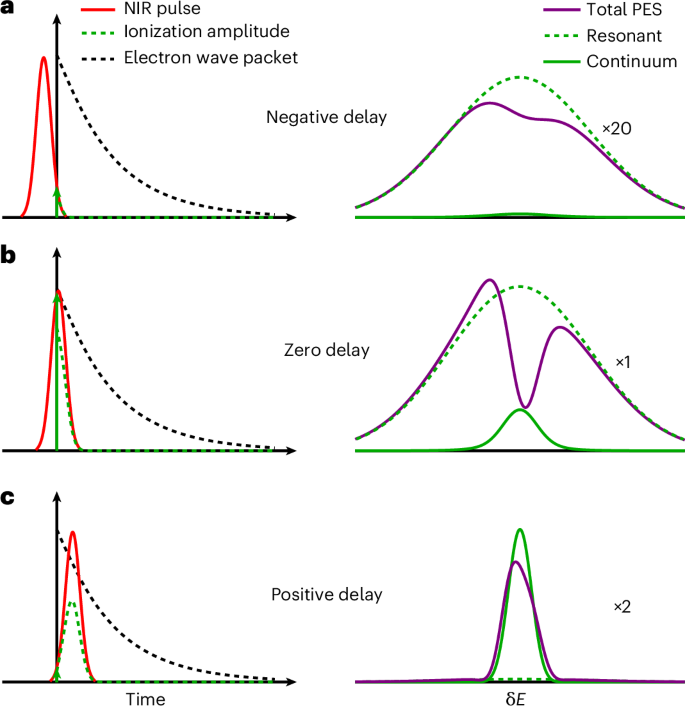
a–c, Schematic illustrations of the evolution of a gated Fano resonance in time (left) and energy (right) for IR pulse delays of −38 fs (a), 5 fs (b) and 64 fs (c) relative to the instant t = 0 fs when the resonant state is populated. The black dashed curves show the evolution of the unperturbed resonance without the IR pulse for reference. The photoelectron spectra are rescaled for a better visualization, with scaling factors of 20 (a), 1 (b) and 2 (c), respectively. The vertical axes in the left and right images represent temporal and spectral amplitudes, respectively. PES, photoelectron spectrum.
Having determined the origin of the sideband pattern, we next reconstructed the full information of the structured EWP (P(t)) using the Griffin–Lim phase retrieval algorithm51. The results in Fig. 3 reveal remarkable agreement between the measured (top row) and reconstructed (bottom row) time-resolved photoelectron spectra, with relative errors of less than 1% when the latter were convoluted with the instrumental response function (see Supplementary Note 1 for details). The requirements and limitations of the retrieval approach are discussed in Supplementary Note 2. The temporal profiles of the reconstructed EWPs, together with the energy profiles, are shown in Fig. 4.
Fig. 3: Time-resolved spectra of resonant EWPs.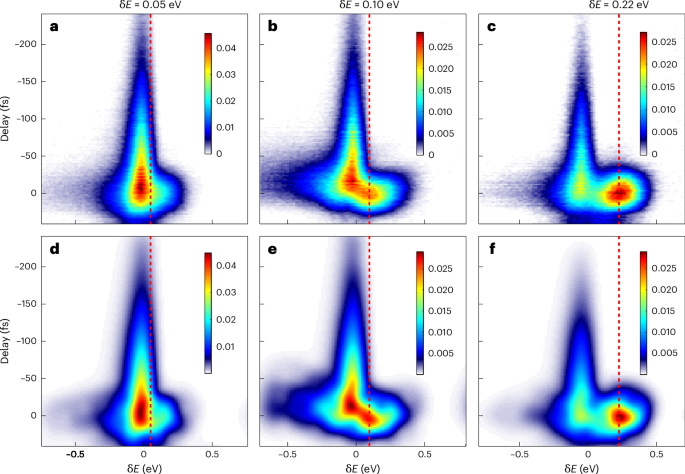
a–c, Measured time-resolved photoelectron spectra for different XUV energies, specified in terms of their detuning (δE) from the resonance. The vertical dashed red lines indicate the estimated central energy of the direct ionization channel. d–f, The corresponding reconstructed time-resolved photoelectron spectra. The origin of the energy axis is adjusted such that the exponential decay tail lies at the centre. The relative errors of the three retrievals are 0.45% (d), 0.71% (e) and 0.77% (f). The colour scales refer to the photoelectron signal in arbitrary units.
Fig. 4: Retrieved amplitudes and phases of the electron wave packets.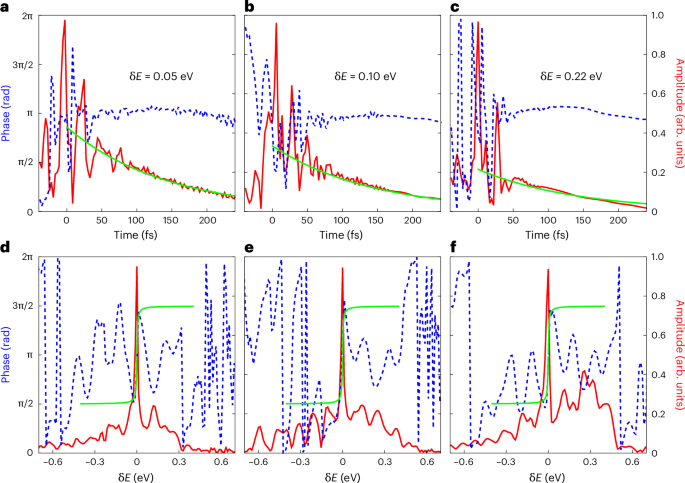
a–f, Temporal (a–c) and energy (d–f) profiles of the resonant EWPs reconstructed from the experimental data in Fig. 3a–c, respectively. The amplitude and phase are represented as solid red lines (right y axes) and dashed blue lines (left y axes), respectively. The solid green lines in a–c represent a logarithmic fit exp(−t/τ) to the amplitude in the time domain. The solid green lines in d–f represent the energy-domain correspondence arctan(δEτ) to phase.
During the temporal overlap of the XUV and NIR pulses, a multi-peak structure emerges in the time evolution of the EWPs (Fig. 4a–c), reconstructed from the experimental delay-gated photoelectron spectra. The reconstructed time evolution reveals substructures that are absent in the simple scheme of the prototypical Fano resonance (Fig. 2), where the instantaneous excitation of the resonance by an idealized ultrashort XUV pulse implies an infinitely wide energy distribution that suppresses all substructures. Interpreted in the time domain, the substructures are due to the interference between the continuum and resonant transitions, with a relative phase δϕ = δE × t determined by the detuning δE between the XUV photon energy and the resonance energy and the time t elapsed since the resonance was populated. As the XUV pump pulse has a finite width, it broadens the continuum transition from a delta function to a Gaussian-like wave packet in the time domain, centred at time 0. As t increases, the resonant state starts to decay into the continuum, modulating the relative contribution of resonant and direct transitions accordingly, which gives rise to either strong destructive or constructive interference according to the phase difference. In the region with a large positive delay, the absence of the XUV-induced continuum path will suppress the interference pattern, reducing the spectrum to its inherent exponential decay profile. More interestingly, these strong electron correlation dynamics can be revealed by comparing the results of different ratios of the resonant and continuum contributions. For all ratios, the local maxima of EWPs consistently align with the EWP phase jumps in the time domain, which highlights the role of the phase difference. As shown in Fig. 4a–c, increased detuning from resonance suppresses the resonant contribution, and thus reduces the temporal extent of the signal oscillations. The Fourier transformations (that is, the energy-domain profiles) of the corresponding EWPs are shown in Fig. 4d–f. The sharp amplitude peak in the centre, together with a π phase jump, which represents the resonant channel, has a typical Lorenz line shape. The continuum channel acts as a broad background, growing in relative amplitude as the detuning increases—as shown in Fig. 4d–f, which displays an increasing background contribution from left to right.
The exponential decay tail of the EWP at large time delays contains information about the lifetime of the autoionizing state, which is conventionally accessed by high-resolution XUV static absorption spectroscopy (that is, at synchrotrons)52,53. We note that a recent study presented a theoretical proposal, together with an ab initio simulation, for determining the lifetime using a similar scheme54. Here we fitted the temporal profile of the squared amplitude with \(\exp (-t/\tau )\) to extract τ. The lifetime obtained, 77 ± 11 fs, agrees well with the results calculated from the linewidth of the static spectroscopic (\({\sim}79.{3}_{-4.5}^{+5.1}\,{\rm{fs}}\))47,48 and time-resolved four-wave-mixing (72.6 ± 6.5 fs)55 measurements. Although the Lorentz-like line shape in energy domain EWPs also contains the lifetime information, direct fitting with an acceptable error is difficult due to the limited energy resolution.
The discrepancy between the reconstructed EWPs from experimental measurements and a typical Fano profile, particularly the oscillating structure in the reconstructed EWPs, can be attributed to two main reasons. First, the time-resolved photoelectron spectrum is obtained by measuring the photoemission from a large acceptance angle. Therefore, this angular-integrated measurement may smear out the intrinsic information originating from the coherent summation of p–s and p–d transitions, the full resolution of which requires angular-resolved observables. Second, as the energy of the final NIR-dressing state (E ≈ −0.507 a.u.) nearly coincides with the single ionization threshold (E2 = −0.5 a.u.) of He(2s/2p), many high-lying Rydberg states may participate in the dynamics56. The involvement of a high density of doubly excited Rydberg states would modulate the photoelectron spectrum through interference between the continuum and multiple resonant states, resulting in a finer distribution in the energy domain. Consequently, the observation of this structure requires a spectral resolution down to a few millielectronvolts.
To conclude, we have developed photoelectron FROG, a powerful method for reconstructing the amplitude and phase of EWPs. We have demonstrated the method on a series of EWPs close to a prototypical Fano resonance with engineered XUV pulses. The evolution of these structured EWPs is captured with high-energy-resolution photoelectron spectroscopy. Given the excellent agreement between our experimental results and the theoretical reconstruction, we expect that this method—combined with high-energy-resolution photoelectron spectroscopy, as applied here—will provide a broadly applicable technique for the complete characterization of structured EWPs. The sensitivity and the robustness of this approach allow us to investigate electron dynamics in the presence of strong electron correlations, including those that involve multiple resonant states. Moreover, the temporal amplitude and phase information provided by the photoelectron FROG framework can be used to coherently control EWPs, paving the way to manipulating electron-dominated dynamics in more complex systems.