Background
In this paper, we consider classes of shallow-depth quantum circuits—circuits of constant depth independent of the input length, using a polynomial number of gates that have bounded fan-in (i.e., each gate has a fixed, constant number of input and output wires) and are drawn from a finite, qudit universal quantum gate set. Over qubits, this class is commonly referred to as \({{\mathsf{QNC}}}^{0}\). Throughout this paper, we refer to qudit systems of prime dimension p as “qupits” (with the associated state space \({{\mathbb{C}}}^{p}\)). Concurrently, we will compare shallow quantum circuits, as efficient and hardware-friendly as possible, with circuits in the \({{\mathsf{bPTC}}}^{0}(k)\) class described by constant depth classical circuits composed of unbounded fan-in gates that compute biased polynomial threshold functions (PTFs), which may be non-linear but are constrained by a bias parameter k26. A PTF with bias k is defined as follows,
$$f(x)=\left\{\begin{array}{ll}P(x),\quad &{\sum }_{i=1}^{n}{x}_{i}\le k\\ 1,\quad &{\sum }_{i=1}^{n}{x}_{i}\, > \, k\end{array}\right.;,$$
(1)
with \(P:{{\mathbb{F}}}_{2}^{n}\to {{\mathbb{F}}}_{2}\) being a polynomial over \({{\mathbb{F}}}_{2}=\{0,1\}\) and k restricting the maximum degree of P. We note that the common definition in the literature takes \(P:{{\mathbb{R}}}_{2}^{n}\to {\mathbb{R}}\), and sets \(f(x)=\frac{1}{2}\left(1+{{{\rm{sgn}}}}\left(P(x)\right.\right)\). On the other hand here we are interested in polynomials of degree at most k over \({{\mathbb{F}}}_{2}^{n}\), with threshold behavior determined by the bias parameter k.
This parameter constrains their behavior to function as the Boolean \({\mathsf{OR}}\) when the input string has a Hamming weight of at least k. Conversely, the behavior can be inverted, in which case the bias parameter constrains it to function as the Boolean \({\mathsf{AND}}\), applying to input strings with a Hamming weight of at most n–k. For a constant, non-zero k (i.e., \(k={{{\mathcal{O}}}}(1)\)), this class corresponds to Boolean circuits with unbounded fan-in \({\mathsf{AND}}\), \({\mathsf{OR}}\), and \({\mathsf{NOT}}\) gates of constant depth, known as the circuit class \({{\mathsf{AC}}}^{0}\)27. Notably, \({{\mathsf{AC}}}^{0}\) represents the largest classical circuit class for which unconditional quantum advantages have been established17. When k = Θ(n), it encompasses the strictly larger \({{\mathsf{TC}}}^{0}\) circuit class.
For intermediate scalings, this class provides access to unbounded fan-in gates with biased yet non-trivial activation regions, see Fig. 1 and refer to SI section D2 for our decomposition algorithm, which translates k biased activation functions into \({{\mathsf{bPTC}}}^{0}(k)\) circuits. Furthermore, it includes majority gates with small fan-in, capturing some of the computational power of \({{\mathsf{TC}}}^{0}\). Notably, even a single biased threshold gate with bias \(k=\omega (\log n)\) is known to require Boolean circuits of superpolynomial size (i.e., \(\Omega ({n}^{{{{\rm{polylog}}}}(n)})\)) using unbounded fan-in \({\mathsf{AND}}\), \({\mathsf{OR}}\), and \({\mathsf{NOT}}\) gates to simulate it26. From this, and given that bounded fan-in constant-depth classical circuits are described by the \({{\mathsf{NC}}}^{0}\) circuit class, we derive the following sequence of inclusions for classical parallel computational classes:
$${{\mathsf{NC}}}^{0}\, \subsetneq\, {{\mathsf{AC}}}^{0} \, \subsetneq \, {{\mathsf{bPTC}}}^{0}(k)\,{{{\rm{for}}}}\,k=\omega (\log n).$$
(2)
Fig. 1: Representation of a k-\({\mathsf{ReLU}}\) gate within \({{\mathsf{bPTC}}}^{0}(k)\), constructed using multiple biased threshold gates (k-\({\mathsf{bT}}\)).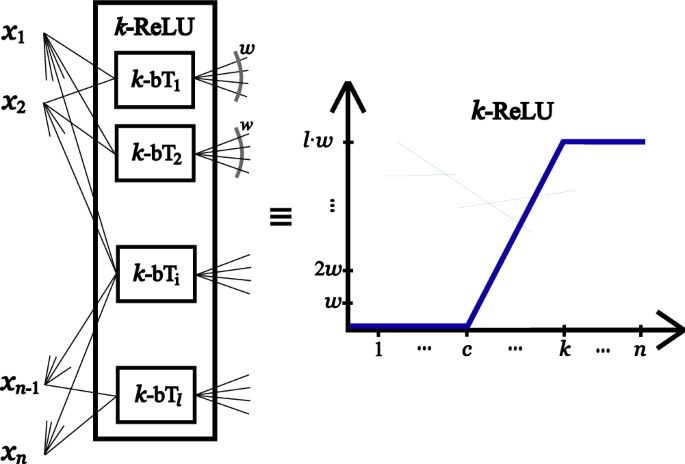
This gate is equivalent to a \({\mathsf{ReLU}}\) gate, defined as \(f(x)=\max \{0,x-c\}\) (where the center is shifted from 0 to c), up to an integer precision w for any input string with a Hamming weight bounded by k. Our scheme considers \({\mathsf{ReLU}}:{\{0,1\}}^{n}\mapsto \{0,n-c\}\), which takes n-bit strings as input and interprets their Hamming weight as the input x.
Thus, we highlight that biased polynomial threshold circuits of constant depth provide a valuable framework for investigating quantum computational power, especially by analyzing the impact of various bias parameters and their practical relevance (see Fig. 2).
Fig. 2: Relationships between the key classical and quantum circuit (complexity) classes considered.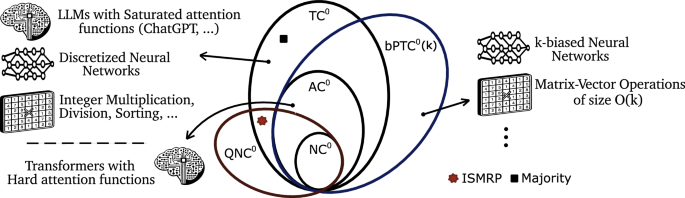
Notably, \({\mathsf{Majority}}\) is in \({{\mathsf{TC}}}^{0}\) but not \({{\mathsf{AC}}}^{0}\). The ISMR family, introduced here, separates constant-depth quantum circuits from biased polynomial threshold circuits (bias \(k=\omega (\log n)\)). The latter class contains \({{\mathsf{AC}}}^{0}\), and can solve \({{\mathsf{NC}}}^{1}\)-complete problems for super-logarithmic biases and input lengths, suggesting non-trivial overlap with \({{\mathsf{TC}}}^{0}\). We also note computational tasks and models of significant practical value, such as neural networks. For example, Large Language Models (LLMs) that use the transformer architecture can be simulated by \({{\mathsf{AC}}}^{0}\) circuits when the attention mechanism is limited in certain natural ways24,77. Meanwhile, \({{\mathsf{TC}}}^{0}\), the standard for modeling discretized neural networks20,78, can simulate LLMs with realistic constraints on variable precision and autoregression25,79,80, in the absence of more complicated elements such as feedback loops. The biased polynomial threshold circuits we study can simulate neural network variants and approximate activation functions controlled by the bias parameter k.
Finally, we focus on relational or search problems, where the inputs x are n-bit strings, and the outputs y are m-bit strings. Formally, we have valid input-output pairs \((x,y)\in {{{\mathcal{R}}}}\) for some relation \({{{\mathcal{R}}}}\subset {\{0,1\}}^{n}\times {\{0,1\}}^{m}\). As in previous results, these relations will have non-local games embedded into them. In this paper, we introduce the family of qudit \({\mathsf{XOR}}\) non-local games, designated Modular XOR games, described in Fig. 3. Building on this class of multi-party non-local games, we introduce a corresponding family of relational problems, that we term Inverted Strict Modular Relation Problems (ISMRP). For any prime p, the ISMR problem \({{{{\mathcal{R}}}}}_{p}\) is defined as follows. Given an input \(x\in {{\mathbb{F}}}_{2}^{n}\) such that \(| x| \,\,\,\,{{{\mathrm{mod}}}}\,\,p=0\), the goal is to output a string from the set
$${{{{\mathcal{R}}}}}_{p}(x):=\left\{y\,\left\vert \,y\in {{\mathbb{F}}}_{2}^{m}:\,| y| \right.=-\left(\frac{| x| }{p}\right)\,{{{\mathrm{mod}}}}\,\,p\right\},$$
(3)
where \(| z|={\sum }_{i=1}^{n}{z}_{i}\) is the ℓ1-norm for any string \(z\in {{\mathbb{F}}}_{p}^{m}\), which is equal to the Hamming weight in the case of bitstrings. We typically choose the output length m to be slightly larger than n.
Fig. 3: Representation of the n-party Modular \({\mathsf{XOR}}\) games \({{{{\mathcal{G}}}}}_{p}\).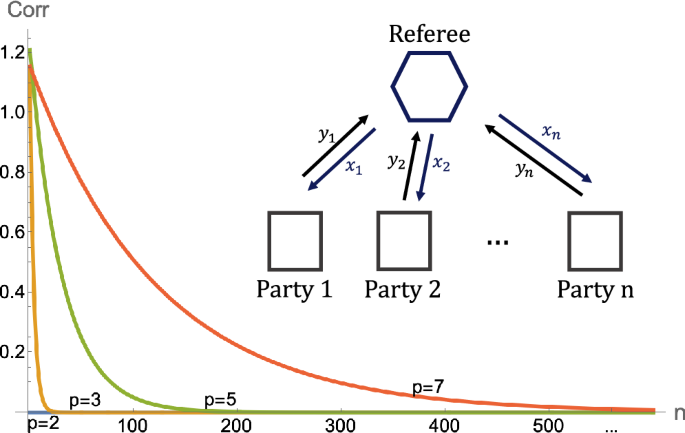
Each party Pi receives an input \({x}_{i}\in {{\mathbb{F}}}_{p}\) from a referee, forming a combined input string x with an ℓ1 − norm ∣x∣ = kp, where \(k\in {\mathbb{N}}\). Without further communication, each party responds with \({y}_{i}\in {{\mathbb{F}}}_{p}\), resulting in a collective output y = (y1, y2, …, yn). The players win if the output y has ℓ1-norm equal to the additive inverse of k modulo p, i.e., \(| y|=-k\,{{\mathrm{mod}}}\,\,p\). For context, \({{{{\mathcal{G}}}}}_{2}\) relates to the Mermin-Peres non-local game used in prior works14,17. The plot illustrates the upper bounds on the (winning) correlation of classical strategies for \({{{{\mathcal{G}}}}}_{2}\), \({{{{\mathcal{G}}}}}_{3}\), \({{{{\mathcal{G}}}}}_{5}\), and \({{{{\mathcal{G}}}}}_{7}\), whereas the optimal quantum strategy attains a maximum correlation of 1 for all \({{{{\mathcal{G}}}}}_{p}\).
These problems possess some intriguing structural properties, as the set of valid output strings is determined entirely by the modular residue of the input’s ℓ1-norm \(\,{{{\mathrm{mod}}}}\,\,p\). To describe how well a circuit can solve this search problem, we employ a correlation measure suited to its modular nature:
$${{\mathsf{Corr}}}_{{{{\mathcal{D}}}}}(f,g)=\mathop{{\mathbb{E}}}_{x \sim {{{\mathcal{D}}}}}\left[{\mathsf{Re}}\left({e}^{i\frac{2\pi | f(x)| -| g(x)| }{p}}\right)\right].$$
(4)
Here \({{{\mathcal{D}}}}\) is a distribution over input strings, and f, g are \({{\mathbb{F}}}_{p}^{m}\)-valued functions. Our notion of correlation for ISMR problems extends standard correlation for Boolean functions to mappings from {0, 1}n to cyclic groups \(({{\mathbb{F}}}_{p},+)\), measuring the deviation between the ℓ1-norm of the true output ∣f(x)∣ and an estimate ∣g(x)∣. Perfect alignment, with \(| f(x)| -| g(x)| \equiv 0\,({\mathsf{mod}}\,p)\), maximizes correlation, while other values decrease correlation, with penalties growing as deviations approach \(\frac{p-1}{2}\). Thus, it accounts for “how wrong” an output is.
Higher dimensional qudits
Qudit-based quantum computation has generated significant interest in recent years, harnessing multidimensional quantum states that are more common in nature compared to two-level systems. They offer greater accuracy and efficiency in information storage and processing, along with improved noise resilience28,29. For example, complex entangled states such as multidimensional Greenberger-Horne-Zeilinger (GHZ) states and cluster states have demonstrated higher noise robustness compared to their qubit counterparts30. Additionally, algorithmic adaptations for qudits have empirically been observed to offer advantages, particularly in quantum simulations of complex systems, where qudits serve as a natural simulation platform. These capabilities have driven the development of qudit-based computing models across various hardware platforms. Moreover, the use of qudits could facilitate quantum advantage experiments that, in turn, may also serve as critical benchmarks for evaluating future quantum devices.
This motivates our first contribution, demonstrating separations in computational power between quantum circuits operating over prime dimensional qudits and biased polynomial threshold circuits of constant depth.
Theorem 1
For every prime p and large enough n, the search problem \({{{{\mathcal{R}}}}}_{p}\) with n-bit inputs and \({{{\mathcal{O}}}}(n\log {(n)}^{p-1})\)-bit outputs admits a constant-depth quantum circuit consisting of local gates over \({{{\mathcal{O}}}}(n)\) “qupits”, consisting of o(n2) gates (i.e., of sub-quadratic size), that has constant correlation with \({{{{\mathcal{R}}}}}_{p}\). In contrast, any polynomial-size biased polynomial threshold circuit of depth d and bias k = n1/(5d), with access to random bits, has exponentially small correlation \(\exp \left(-\Omega \left({n}^{3/5-{{{\mathcal{O}}}}(1)}\right)\right)\) with \({{{{\mathcal{R}}}}}_{p}\).
As noted, biased polynomial threshold circuits serve as a useful theoretical model for neural networks, and the extent of expressivity and computational power modeled by such circuits is controlled by the bias parameter. Our results demonstrate that biased threshold circuits with bias parameter values satisfying \(k={{{\mathcal{O}}}}({n}^{1/d})\), require superpolynomial size to solve a relational problem that small quantum shallow-depth circuits over qupits solve efficiently. This strengthens the provable quantum advantages over classical models with significantly more computational power than those in prior studies14,17,31 (see also Eq. (2)). Crucially, we prove our bounds for the maximum bias parameter for the search problems considered—any larger bias k would enable these circuits to efficiently compute functions like parity and solve the problem with high probability using linear-sized circuits. Thus, our results push the possible quantum advantage against to this class of circuits, in terms of bias, to its theoretical limit.
Previous studies have suggested that qudit non-local games with significant gaps in quantum versus classical winning probabilities could imply computational separations between classical and quantum circuit classes32, though such separations were not explicitly demonstrated. In Theorem 1, the family of relational problems \({{{{\mathcal{R}}}}}_{p}\) for each prime dimension corresponds to a family of Modular \({\mathsf{XOR}}\) non-local games that we define (Fig. 3). For these non-local games, we constructively prove that classical strategies achieve, at best, exponentially lower success probabilities than quantum strategies as the number of parties increases. The translation to quantum computational advantage is then achieved using shallow-depth quantum circuits in each prime qudit dimension over a corresponding standard, minimal finite gate set, with the precise instantiation of these circuits provided in the Supplementary Information (SI) Section B2. This approach broadens quantum advantages to an infinite family of problems and demonstrates the feasibility of implementing constant-depth realizations of such advantages on existing quantum hardware.
We also emphasize that this separation is achieved in the setting of average-case hardness with uniform input distributions over binary inputs. To do this, our method elegantly manages non-uniform input distributions for qupit non-local games, handling the necessary dit-to-bit mappings to ensure that we use uniform (rather than biased) random restrictions for the biased polynomial threshold circuits. This approach allows us to obtain average-case \({{\mathsf{bPTC}}}^{0}(k)\) hardness with respect to the uniform distribution on binary inputs for the search problems that demonstrate the separation. Additionally, it avoids the need to compute explicit success probability bounds for each game. In particular, we show that for our family of games parameterized by a prime p, the correlation of any classical strategy with a winning answer decreases exponentially with the number of parties in the game (see Section IV A). This correlation decay alone is sufficient to achieve comparable separations. We thus sidestep the obstacle of explicitly computing bounds on winning probabilities: this has been emphasized in prior research, which predominantly relied on established quantum-classical distinctions in the winning probabilities for non-local games14,17. Few developments beyond the conventional qubit setting were considered or achieved previously33. Finally, our search problems \({{{{\mathcal{R}}}}}_{p}\) remain binary, aligning naturally with Boolean circuits. They do not impose hardness by making clever use of arithmetic operations over other prime fields, making traditional Razborov-Smolensky type lower bounds inapplicable to this classical Boolean gate setting.
For the quantum solutions, we have generalized a method that translates optimal quantum strategies for these non-local games into small constant-depth quantum circuits that address the corresponding qupit search problems. We specifically leverage the use of generalized GHZ states in optimal strategies and the ability to generate multipartite entanglement between non-neighboring qupits in constant depth. We have derived local unitary (LU)-equivalent generalized GHZ states and introduced a technique to efficiently describe the support of standard measurement outcomes of these states, factoring in phase dependencies. This enables us to use them in combination with an additional correction function that is computable in constant depth, approximating the outcome of the optimal quantum strategy. Moreover, it facilitates the determination of the success probability, highlighting the quantum circuits’ superiority over classical approaches.
To understand the potential advantages of parallel quantum computation, we first need a candidate problem with an efficient quantum solution. A significant part of the challenge subsequently lies in proving lower bounds on the resources (for example, the circuit size or depth) required by the corresponding classical parallel models to solve this problem. Our approach introduces a novel multi-output multi-switching lemma that serves as a reduction tool, breaking down multi-output biased polynomial threshold circuits into simpler classical computational models, such as decision trees, to which locality and light-cone arguments can be applied (see Section IV A). In Theorem 1, this new lemma plays a pivotal role by simplifying these circuits into forms that reveal their locality, directly linking their performance to the optimal classical strategies for the corresponding non-local games. More broadly, as these tools address not only binary decision problems but also search-type problems, this technique may hold independent significance, as neural networks are fundamentally sequence-to-sequence models. Therefore, this approach can be applied to relational problems beyond those examined here. Furthermore, parameterization by the bias parameter k provides a continuum of classical computational power levels, allowing for broader applicability. In particular, we use this framework to clarify the relationship between hardware requirements and the potential for quantum advantage.
Qubits
Among all prime qudit dimensions, only two—p = 2 and p = 3—allow for an intuitive translation from quantum lower and classical upper bounds on correlations to corresponding bounds on success probabilities. Specifically, our results show that polynomial-size biased polynomial threshold circuits (of small bias) cannot solve the \({{{{\mathcal{R}}}}}_{2}\) and \({{{{\mathcal{R}}}}}_{3}\) problems with success probabilities appreciably larger than 1/2 and 1/3, both of which correspond to random guessing. In contrast, quantum circuits can solve the qubit case exactly, while in the qutrit case, the problem is solvable with a probability larger than and bounded away from 1/2 by a constant.
In the qubit case, we can in fact demonstrate something stronger: that if classical circuits are required to solve \({{{{\mathcal{R}}}}}_{2}\) exactly—that is, to produce a valid output string with certainty for all inputs—quantum advantages or separations of even greater magnitude are attained.
Theorem 2
For large enough n, the search problem \({{{{\mathcal{R}}}}}_{2}\) with n-bit inputs and \({{{\mathcal{O}}}}(n\log n)\)-bit outputs can be solved by a constant-depth qubit quantum circuit with o(n2) gates, which on any valid input x outputs y such that \((x,y)\in {{{{\mathcal{R}}}}}_{2}\) with certainty. In contrast, the size s of any depth-d k-biased polynomial threshold circuit, with access to random bits, that computes any valid y is lower bounded as in Table 1.
Table 1 Lower bounds on the size of \({{\mathsf{bPTC}}}^{0}(k)\) circuits solving the \({{{{\mathcal{R}}}}}_{2}\) problem, for different regimes of the value of k
We remark that this exact-case analysis is well-motivated by the fact that the quantum circuit in the qubit case is actually a deterministic solution to \({{{{\mathcal{R}}}}}_{2}\), and therefore it is fair to compare it with classical deterministic circuits—to draw a complexity theoretic analogy, this is similar to comparing \({\mathsf{EQP}}\) and \({\mathsf{P}}\), as opposed to the more common comparison of \({\mathsf{BQP}}\) and \({\mathsf{BPP}}\). We also note that for \(k={{{\mathcal{O}}}}(1)\), constant-depth k-biased polynomial threshold circuits are equivalent to constant-depth logical circuits with unbounded fan-in Boolean gates (i.e., \({{\mathsf{AC}}}^{0}\)), and so our bounds in the exact-case augment and improve on prior work17.
In proving Theorem 2, we have developed a technique to capture the classical-quantum circuit separation using the algebraic normal form (ANF), a standard representation for Boolean functions (see Section IV B). Importantly, this approach avoids the need for non-local or contextual games32, which have traditionally been essential in prior work, while also showing that previous quantum advantages might benefit from new techniques to improve resource requirements and bring them closer to practical quantum demonstrations.
We thus derive two lower bounds on the classical circuit size in the qubit setting. The most robust demonstration of quantum advantage arises in the setting of average-case hardness, where deviations of the classical success probability away from random guessing can be directly bounded. However, our exact-case hardness analysis reveals a quantum advantage of a greater magnitude, establishing higher resource requirements for classical circuits to match the performance of the quantum circuits they must compete with. This suggests that quantum advantage experiments against shallow-depth classical circuits could be achieved with fewer resources.
Noise-robustness
Finally, quantum systems are unavoidably affected by noise, and error correction is a much more complex process in the quantum realm, bringing into question the robustness of a computational advantage under noise. This question is of significance to both theory and practice, especially as we navigate the NISQ era. Even for very powerful quantum computational models, the introduction of noise often dramatically diminishes computational advantages that they may offer over their classical counterparts: for instance, recent work shows that even small constant error rates result in a collapse of the power of multi-prover interactive proofs where the provers share entanglement (\({{\mathsf{MIP}}}^{*}\)) from \({\mathsf{RE}}\) to multi-prover interactive proofs without shared entanglement (\({\mathsf{MIP}}\))34. Our third main result is to prove that all our separations are robust to noise: even if all steps of the quantum computation are affected by local stochastic noise, there is a family of modified relation problems that these noisy quantum circuits, when provided with logical magic states, can solve, but is hard for noiseless \({{\mathsf{bPTC}}}^{0}(k)\) circuits.
Theorem 3
For every prime p and large enough n, there exists a search problem \({{\mathfrak{R}}}_{p}\) with n-bit inputs and \({{{\mathcal{O}}}}(n\cdot {\mathsf{poly}}(\log n))\)-bit outputs, such that for local stochastic noise with physical error rate below a constant threshold, there is a noise-resilient constant-depth quantum circuit over qupits with local gates and all-to-all connectivity, equipped with logical \(\left\vert {T}^{1/p}\right\rangle\)-magic states, that has constant correlation with \({{\mathfrak{R}}}_{p}\). In contrast, any (even noiseless) depth-d polynomial-size biased polynomial threshold circuit with bias k = n1/(5d) has exponentially small correlation \(\exp \left(-\Omega \left({n}^{3/5-{{{\mathcal{O}}}}(1)}\right)\right)\) with \({{\mathfrak{R}}}_{p}\).
The search problem \({{\mathfrak{R}}}_{p}\) is defined using the ISMR problem \({{{{\mathcal{R}}}}}_{p}\), accounting for quantum error correction (see SI Section C).
Local stochastic noise is a standard model used in quantum error correction, favored due to its ability to account for gate-level noise, noisy input state preparation, and noisy measurements while allowing for (weakly) non-local errors. Locality means that the probability of any given Pauli error decays exponentially with the number of sites it affects non-trivially. Additionally, this model effectively captures fabrication faults and aligns with standard physical descriptions of noise, wherein errors become exponentially less probable as their weight increases35. Theorem 3 proves that our computational separations are robust to the presence of qupit generalized local stochastic noise in the quantum circuits.
This result improves upon prior work in three main ways. First, it extends unconditional separations between noisy, shallow-depth quantum circuits and classical circuit classes. In particular, this is achieved for all prime qudit dimensions and against the largest classical circuit class to date. Notably, while most qudit dimensions require logical T-type magic states as advice in the general formulation of Theorem 3, we have also demonstrated a noise-resilient quantum advantage using Clifford circuits over qubits that do not rely on such advice. Additionally, as a corollary, this establishes separations against \({{\mathsf{NC}}}^{0}\) for each prime qudit dimension, potentially enabling near-term quantum advantage experiments due to the reduced resource requirements for this class and the favorable error-resilience properties of qudits.
Second, our approach extends the framework for noise-robust quantum advantages beyond the qubit Clifford model introduced in ref. 16, by addressing qudit non-Clifford gates. Specifically, we demonstrate that for a particular CSS-type error correction code, this extension is achievable through the use of logical T-type magic states, which can themselves be affected by local stochastic noise, along with qudit magic-state injection protocols (see Section IV C). The need for these more complex quantum circuits arises from the inability to violate Bell inequalities with stabilizer states for any qupit dimension beyond qubits, as shown in refs. 36,37,38, which also suggests that the same limitation extends to quantum-classical separations in circuit complexity. Additionally, as part of Theorem 3, we design new quantum circuits in the form of non-adaptive Clifford circuits with input-independent advice states to solve ISMR problems fault-tolerantly. These quantum circuits essentially give rise to our definition of the \({{\mathfrak{R}}}_{p}\) search problems.
Third, our work extends shallow-depth computational separations and error-correction mechanisms across arbitrary prime qudit dimensions, demonstrating their robustness. Previous research used the minimum weight perfect matching decoder, which performs poorly in higher dimensions. By using a different decoder, we show that we can still perform corrections and recover the desired states with exponentially high confidence. Specifically, we illustrate how the qupit surface code, when combined with the hard decision renormalization decoder, supports fault-tolerant implementation of the necessary quantum circuits. This advancement includes the development of single-shot logical state preparation for qupits. We have also extended the 3D block construction from39 to higher dimensions, showing that a particular measurement pattern yields a reduced state corresponding to a logical GHZ2 state, up to local Clifford corrections.
Resource estimates
When testing computational advantages with physical implementations, it is essential to pinpoint the circuit depth d and input size n (i.e., the number of input qubits) where a transition in circuit size occurs. Specifically, at what depths and input sizes does quantum advantage emerge? To address this, we estimate these values by solving for the points where our new asymptotic lower bounds on the size of the best classical circuits match our corresponding quantum upper bounds. In Table 2, we present the input size n for a given depth d, corresponding to the shallowest quantum circuits (with all-to-all connectivity) in each qudit dimension that outperform their classical counterparts in solving the respective ISMR problems.
Table 2 Estimates of the input sizes n required to demonstrate quantum advantage using constant-depth quantum circuits in both noise-free and noise-affected settings, based on the quantum upper and classical lower bounds determined in Section II B, Section II C, and Section II D
For context, the transition point for Shor’s factoring algorithm is estimated to be ~1700 qubits, 1036 Toffoli gates, and a circuit depth of 1025 40, while for the HHL quantum matrix inversion algorithm it is roughly 108 qubits and a depth of 1029 10.
In comparison, recent advances in quantum hardware have prioritized scaling up the number of qubits over extending coherence times, leading to a greater emphasis on shallower quantum circuits5,41. Notably, the quantum advantages over constant-depth classical circuits with bounded fan-in gates, as studied in this work, require only thousands of qudits across various dimensions. These setups can demonstrate classical intractability in tasks such as Bell violations42,43. Classical circuits for these problems must have a depth of at least \(d=\Omega (\log n)\), showing a clear quantum advantage when a quantum circuit solves the same problem at a strictly smaller depth. In practical scenarios with noise, the quantum circuit depth may increase by a constant factor, while the minimal classical circuit depth remains at least \(d=\Omega (\frac{\log n}{\log \log n})\). These noise-driven increases in the input size and other parameters required to observe quantum advantage is still significantly smaller, in terms of total resource counts, than what is required in other previous quantum advantage demonstrations.
Progressing up the hierarchy of computational power toward demonstrations of unconditional quantum advantage, the challenge lies in outperforming larger classical constant-depth circuit classes, such as biased polynomial threshold circuits. Achieving such quantum advantages would require significantly greater quantum resources, yet could still compare favorably to other conditional quantum advantage demonstrations in noise-free settings. These quantum circuits maintain the advantage of shallow depth, potentially making them more practical for near-term quantum hardware. However, comparisons between noise-affected quantum circuits and noise-free classical circuits often demand unrealistic resources, exposing a fundamental imbalance in such analyses. Classical computing benefits from decades of refinement, and classical error-correcting codes may also be necessary to achieve exponentially high efficiency rates akin to those expected of error-corrected quantum circuits44. Although noise levels in quantum and classical systems are unlikely to converge6,45,46, resource estimates that account for noise on both sides—combined with advances in quantum hardware—are anticipated to bring these comparisons closer to what is expected from noise-free quantum models.
Beyond the estimates in Table 2, our bounds extend to all prime qudit dimensions and explore quantum circuits with varying hardware connectivities. In noise-resilient scenarios, all-to-all connectivity is required, while in noise-free comparisons, architectures can range from p + 1-dimensional configurations for qudit dimension p to full all-to-all connectivities. Among these, our estimates represent the lowest obtained for equivalent unconditional quantum separations, with the qubit case achieving the smallest resource requirements due to our analysis of exact-case hardness bounds. As mentioned before, while this setting reflects a less robust form of quantum advantage it nevertheless significantly reduces resource requirements, bringing theoretical predictions closer to the capabilities of current quantum devices. These estimates could be improved for all qudit dimensions by requiring classical circuits to better match the performance of the quantum circuits, and by adding connectivity restrictions to classical circuits. While these constraints are not formally part of the definition of shallow-depth circuit classes such as \({{\mathsf{NC}}}^{0}\), they reflect the limitations of realistic classical hardware and could lower the input size needed to demonstrate quantum advantage47. More generally, tighter lower-bound techniques and the discovery of computational problems with greater quantum advantages could further refine these estimates.
Finally, our estimates indicate that these quantum advantage experiments could serve as powerful quantum benchmarks, providing a systematic framework for evaluating and comparing computational capabilities. To explore larger quantum computational advantages, one could test classical circuits with larger fan-in gates, establishing new benchmarks and creating a structured “ladder of quantum advantages” to assess increasingly stronger computational separations. This hierarchy can be expanded by examining the ability of shallow quantum circuits to outperform more advanced classical circuit classes, such as the biased polynomial threshold circuits analyzed in this work. Adjusting the bias parameter within these circuits further allows one to tune or amplify potential quantum advantages offered by specific quantum circuits and architectures. Notably, the levels within both hierarchies are separated by small multiplicative factors, making them an effective tool for benchmarking hardware improvements and guiding steady progress in quantum computing.