We investigated the effect of nanocrystal size on optical properties, focusing on the radiative lifetime. Over 30 high-quality nanocrystals samples were synthesized following a modified version of previous reports (details in the Method section) to minimize non-radiative pathways and to directly extract the radiative lifetime. Figure 1a shows absorption and photoluminescence spectra of CsPbBr3 nanocrystals in the strong, intermediate, and weak confinement regime. Figure 1c–e show their corresponding Transmission Electron Microscopy (TEM) images (larger area shown in Figure S2) along with calculated size distributions26, illustrating highly monodisperse ensemble. Photoluminescence Full-Width at Half Maximum (FWHM) and Stokes shift are extracted for different nanocrystal sizes revealing a linear trend. Both the FWHM and Stokes shift exhibit an increase as nanocrystal sizes decrease, which has been observed previously27,28. This linear trend is correlated between the size of the nanocrystals and the strength of coupling to high-energy optical phonons (2–17 meV)28,29. Specifically, smaller nanocrystals exhibit stronger coupling to these phonons due to enhanced charge density and subsequent polaron formation30. This coupling results in large fluctuations in the bandgap31, consequentially causing broader emission linewidths and larger Stokes shift as evident in Fig. 1a and b.
Fig. 1: Optical and structural characterizations of CsPbBr3 nanocrystals with varying sizes.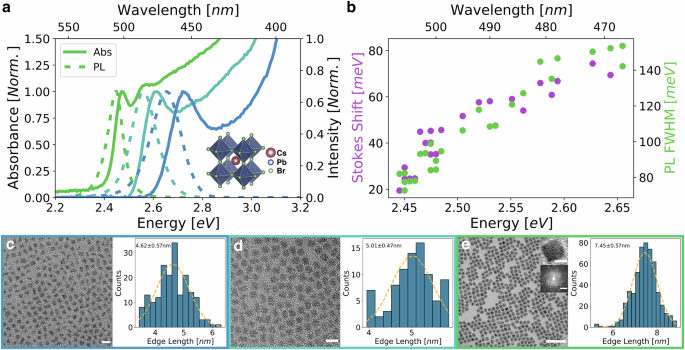
a steady-state absorption, and photoluminescence (PL) spectra of selected nanocrystals in weak, intermediate, and strong quantum confinement regime, with inset showing the crystal structure created with Vesta38. b Stokes shift and full width at half max as a function of bandgap energy are plotted displaying a linearly increasing trend as nanocrystal sizes decrease. c–e are transmission electron microscope (TEM) images along with their corresponding size distributions fitted with gaussian curve to extract the average nanocrystal size. TEM images scale bars are as follow: (c) 10 nm, (d) 10 nm, and (e) 50 nm with inset showing high resolution TEM of a single nanocrystal with 5 nm scale bar and its corresponding Fast Fourier Transform (FFT) with 2 nm−1 scale bar.
Each synthesized distinct nanocrystal sample underwent characterization to determine photoluminescence quantum yield (PLQY) and time-resolved photoluminescence (TRPL) to quantify the radiative lifetime (\({\tau }_{r}\)), which is inversely related to the radiative rate (\({\kappa }_{r}\)), using the following relation:
$${PLQY}=\frac{\frac{1}{{\tau }_{r}}}{\frac{1}{{\tau }_{r}}+\frac{1}{{\tau }_{{nr}}}}=\frac{\frac{1}{{\tau }_{r}}}{\frac{1}{\left\langle \tau \right\rangle }}$$
(1)
$${\tau }_{r}=\frac{\left\langle \tau \right\rangle }{{PLQY}}$$
(2)
$${\kappa }_{r}=\,\frac{1}{{\tau }_{r}}$$
(3)
where \(\left\langle \tau \right\rangle\) is total lifetime extracted by deconvoluting with the instrument response function (IRF) and subsequentially fitting the initial two decades of TRPL decays, as shown in Fig. 2, using a monoexponential function as follow:
$$I\left(t\right)=\,{\int }_{\infty }^{t}{IRF}\left({t}^{{\prime} }\right)*A\,{e}^{-\frac{t-{t}^{{\prime} }}{\tau }}\,d{t}^{{\prime} }$$
(4)
Fig. 2: Time-resolved photoluminescence (TRPL) characterization.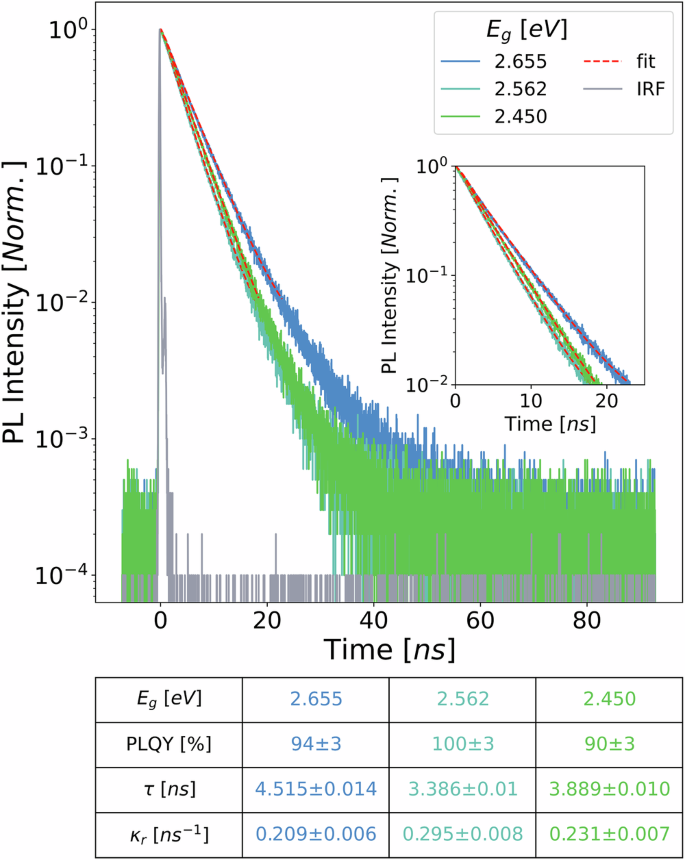
Three selected nanocrystals sizes in strong, intermediate, and strong quantum confinement regimes are assessed using TRPL. Decays are deconvoluted with instrument response function (IRF) and the initial two decades are fitted to a monoexponential function to extract the total lifetime (inset). Absolute photoluminescence quantum yield (PLQY) was measured to calculate the radiative rates for each nanocrystals. The resulting data, including bandgap (Eg), PLQY, total lifetime, and radiative rate, are tabulated, revealing a non-monotonic trend that emerges in lifetimes and radiative rates.
The tabulated data in Fig. 2 show the near-unity PLQY CsPbBr3 nanocrystals across the three confinement regimes. Notably, the strongly and weakly confined nanocrystals exhibit longer radiative lifetime (or slower radiative rate) compared to the intermediately confined nanocrystals.
We conducted further measurements of PLQY and TRPL across different nanocrystal sizes within each of the three confinement regimes under ambient conditions (Supplementary Figs. S3, and S4). Surprisingly, our findings reveal a non-monotonic trend in both radiative lifetime and radiative rate, as shown in Fig. 3a and b. We find, in confirmation of earlier reports16, that the weakly confined nanocrystals exhibit longer radiative lifetimes. Unexpectedly, our measurements on strongly confined nanocrystals display similar long radiative lifetimes. Interestingly, we observe the shortest radiative lifetimes within the intermediate confinement regime. Thus, there exists some optimal nanocrystal size for applications where fast radiative recombination is desirable.
Fig. 3: Size-dependent exciton radiative lifetimes and rates of CsPbBr3 nanocrystals.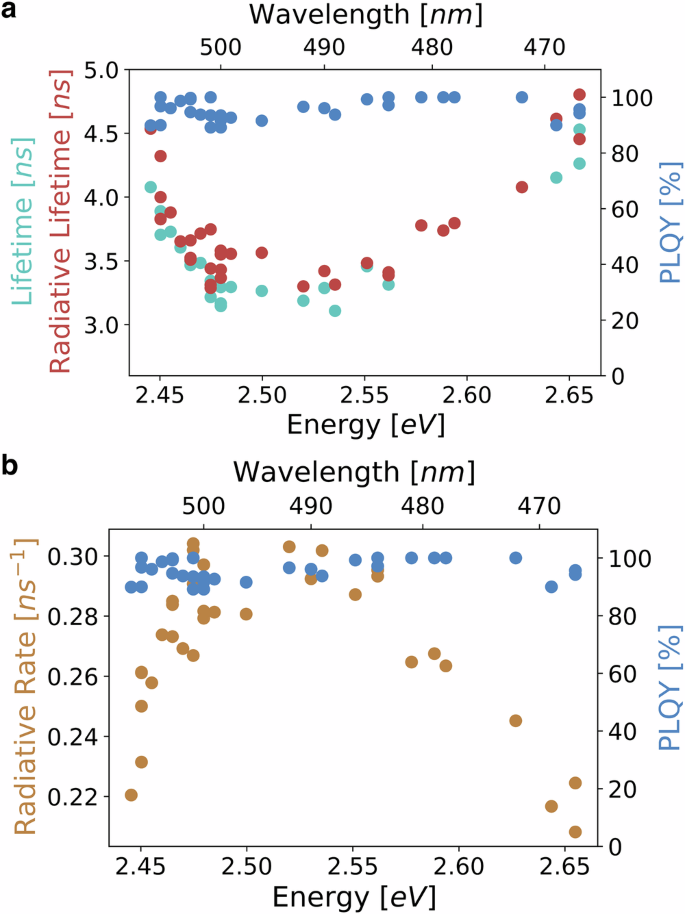
a Measured total lifetime under ambient conditions along with calculated radiative lifetimes via the absolute photoluminescence quantum yield (PLQY) as a function of nanocrystal size exhibit an unexpected non-monotonic trend. Larger nanocrystals in weak confinement regime show lengthened radiative lifetimes that decrease as the nanocrystal size transition into the intermediate confinement regime. Surprisingly, the trend reverses with decreasing nanocrystals size reaching the strong confinement regime. b radiative rates, the inverse of radiative lifetimes, showcasing an optimal size associated with maximum radiative rate.
To understand the underlying factors that may contribute to the lengthened radiative lifetime, we delved into a comprehensive examination of the crystal structure. In Fig. 4a, the powder X-ray diffraction (XRD) patterns of the nanocrystals with sizes spanning the three confinement regimes are illustrated. The nanocrystals in the strong confinement regime exhibit a cubic phase. As the size of the nanocrystals increases, a transition into an orthorhombic phase is observed21,22,23,24,25. This phase transition, as discussed below, is further corroborated by molecular dynamics simulations at 300 K, as shown in Fig. 4b.
Fig. 4: X-ray diffraction (XRD) and molecular dynamics (MD) of varying CsPbBr3 nanocrystal sizes.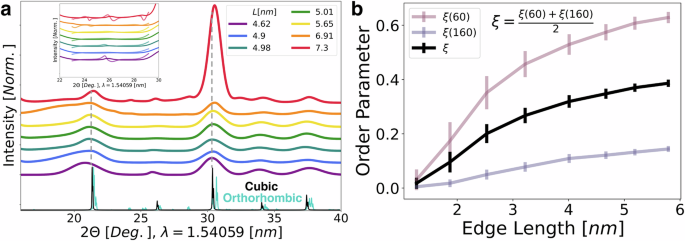
a XRD patterns illustrating the transition from cubic to orthorhombic symmetry. b a composite order parameter that assesses the degree of crystal phase computed from MD simulation trajectories under ambient conditions in reference to a perfect cubic and orthorhombic symmetry, where 0 indicates a cubic and 1 means an orthorhombic symmetry. Error bars denote the variance of the order parameter due to fluctuations in 100 sampled geometries over the simulation. The order parameter results align with XRD patterns, confirming the size-dependent phase transition from being cubic in small nanocrystals to orthorhombic in larger nanocrystals.
Molecular dynamics simulations as implemented in LAMMPS were performed on CsPbBr3 nanocubes with edge lengths of 2 – 6 nm using a previously parametrized force field32,33. The average structural symmetry at 300 K was computed over nanosecond simulation lengths to resolve the size-dependent phase behavior. To produce a quantitative metric of the structural symmetry, we define a local order parameter, \(\xi\), that distinguishes the common cubic and orthorhombic phases of CsPbBr3 nanocrystals. The order parameter is defined on the probability distribution of nearest neighbor halide-halide-halide (X-X-X) angles of the nanocrystal configuration,
$${\xi }_{i}\left(\theta \right)=\frac{[{P}_{i}\left(\theta \right)-{P}_{{cubic}}^{\circ }{\left(\theta \right)}]^{2}}{[{P}_{{ortho}}^{\circ }\left(\theta \right)-{P}_{{cubic}}^{\circ }{\left(\theta \right)}]^{2}}$$
(5)
where \({P}_{i}(\theta )\) is the probability of finding an X-X-X angle of \(\theta\) in the \(i\)-th trajectory step, and \({P}^{\circ }(\theta )\) is the probability of observing angle \(\theta\) in the perfectly symmetric structure. If the configuration along the trajectory possesses cubic symmetry, then the order parameter becomes zero. If the configuration is orthorhombic, the ratio of terms is unity, and the order parameter is one. The averaged order parameter for a certain size, \(\langle \xi \left(\theta \right)\rangle\), is estimated over the simulation trajectory, and we compare it against perfectly cubic and orthorhombic nanocubes of the same size.
The probability distribution of X-X-X angles distinguishes strongly between cubic and orthorhombic CsPbBr3 at two angles, 60° and 160°. For perfectly cubic perovskites, 1/6 of the angles are 60° while zero angles are 60° for perfectly orthorhombic structures. This is reversed at 160°, where perfectly cubic structures have no probability and orthorhombic structures have a 1/6 probability. Supplementary Figure S5 shows histograms illustrating the probabilities, allowing for a clear distinction of certain angles that specifically emerge in one phase but are absent in the other. We develop a composite measure of the size-dependent phase behavior of perovskite nanocrystals in our simulations by averaging \(\xi ({60}^{\circ })\) and \(\xi \left({160}^{\circ }\right)\) over a narrow angular bin:
$$\xi=\frac{\xi \left({60}^{\circ }\right)+\xi ({160}^{\circ })}{2}.$$
(6)
As evident in Fig. 4b, the smaller nanocrystals, characterized by strong quantum confinement, display a cubic structure. As the nanocrystals size increases, a transition occurs, with the average nanocrystal structure progressively shifting towards orthorhombic symmetry–results that closely align with the experimental XRD patterns shown in Fig. 4a. Simulations were also performed on analogous CsPbI3 perovskite nanocrystals and a similar phase behavior was observed. Comparative analysis of the size-dependent anisotropy for CsPbBr3 and CsPbI3 nanocrystals is presented in Supplementary Fig. S6.
Further theoretical understanding of the interplay between perovskite structural and optical properties was gained by performing atomistic electronic structure calculations on the relaxed structures for varying nanocrystal sizes. Accurate electron and hole quasiparticle states including spin-orbit coupling effects were computed within the semi-empirical pseudopotential framework as described in previous reports (Supplementary Fig. S7)34. We obtain a validated pseudopotential from Weinberg et al. describing local, nonlocal and spin-orbit coupling effects for CsPbI334. Electron-hole correlation was included by solving the Bethe-Salpether equation (BSE) within the static screening approximation, which describes excitons in the basis of electron-hole product states35. The electronic properties of CsPbI3 and CsPbBr3 show analogous trends36; thus, we compute radiative lifetimes using the validated CsPbI3 model as a proxy to understand the measured CsPbBr3 radiative lifetimes. Massively parallel software implementations were developed to enable investigation of nanocrystals spanning the strong to intermediately confined regimes, with edge lengths ranging from 2–7 nm. In addition to systems with cubic and orthorhombic symmetry, we relax nanocrystal structures at 0 K using the previously parametrized force field to obtain static input geometries32. It was verified that the 0 K structures show the same size dependent phase behavior as the 300 K simulations (Supplementary Fig. S6). This gives us three structures to compare for each size: cubic, orthorhombic, and relaxed.
We calculated the thermally averaged radiative lifetime in the time-dependent perturbation theory framework as:
$${{{\langle }}\tau }_{r}{{\rangle }}=\frac{1}{{{\langle }}{\kappa }_{r}{{\rangle }}}={\left.\left[\frac{1}{Z}\sum _{n}{e}^{-\beta {E}_{n}}\frac{{{\omega }_{n}}^{3}{\left|{\mu }_{n}\right|}^{2}}{3\pi {\varepsilon }_{o}{{\hslash }}{c}^{3}}\right.\right]}^{-1}$$
(8)
where \({\varepsilon }_{o},\hslash,{c}\) are the vacuum permittivity, reduced Planck’s constant, and speed of light, respectively. The parameters \({\omega }_{n}\) and \({\mu }_{n}\) correspond to the transition frequency and the transition dipole strength of exciton n. Reported radiative lifetimes are the Boltzmann thermal average over excitons. An exciton basis consisting of a few thousand electron and hole product states converges the exciton radiative rates from the BSE, yielding radiative lifetimes that agree well with experiments. A non-monotonic trend in the radiative lifetime is observed as the nanocrystal size increases from the strongly to the intermediately confined regime (Fig. 5a). Uniquely, our atomistic calculations capture this behavior across the size range, showing excellent agreement with experiment for both small and larger perovskite nanocrystals. The lifetime decreases between 2—5 nm, and we rationalize this decrease in radiative lifetime by analyzing the size-dependent oscillator strength of bright states. We find an increase in the oscillator strength of the lowest bright state as the nanocrystals size increases, independently of crystal symmetry (Fig. 5c). However, this does not cause the large nanocrystals approaching weak confinement to exhibit a reduced radiative lifetime. Instead, due to the increasing density of states (DOS) in larger nanocrystals, high-lying states exhibiting weak oscillator strength (i.e., dim states) become thermally accessible and lead to a decreased Boltzmann population of the bright triplet manifold of states (Fig. 5b). We underscore that the non-monotonic behavior depends sensitively on the exciton level details and ambient temperature conditions. We find that at lower temperatures, our model predicts a monotonically decreasing size-dependence of the radiative lifetimes (Supplementary Fig. S8) because the high-lying dim states become thermally inaccessible, in alignment with previously reported experimental findings13,15.
Fig. 5: Size-dependent radiative lifetimes calculation.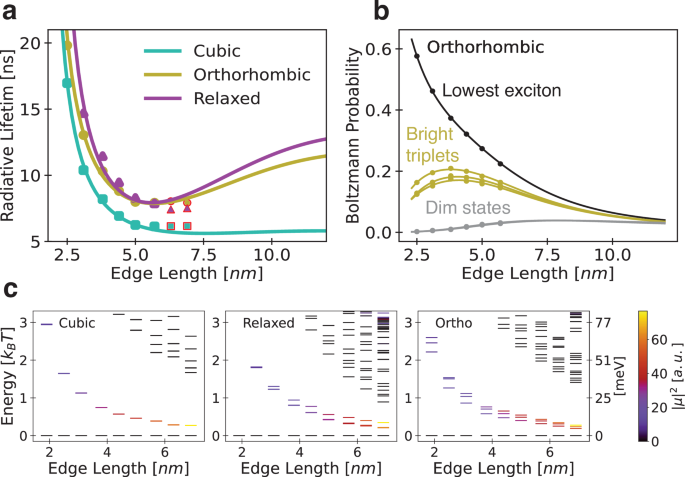
a Calculated size-dependent radiative lifetimes for cubic (teal squares), relaxed (purple triangles) and orthorhombic (gold circles) CsPbI3 nanocrystal structures with corresponding radiative lifetime extrapolations from fits of the exciton energies and oscillator strengths (lines). Only the energies and oscillator strengths of the first six sizes are fitted, and the test points (red ringed points) demonstrate non-monotonicity in the radiative lifetimes and fair agreement with the extrapolated trend. b Size-dependent Boltzmann probabilities of the dark ground state (black), bright triplet states (gold), and high-lying dim states (gray) show depopulation of the emissive triplets in large nanocrystals. c Calculated excitonic states as a function of nanocrystal size plotted for cubic, orthorhombic, and relaxed structures. Here, states within \(3{\kappa }_{B}T\) above the lowest exciton levels are visualized. The color of each state encodes indicates the exciton transition dipole square magnitude (proportional to oscillator strength) in atomic units [a.u.], which increases for the bright excitons with increasing nanocrystal size.
The nanocrystal crystal structure influences the exciton level details. The cubic geometries host degenerate excitons and large bright-dim gaps, while symmetry lowering to the relaxed and orthorhombic structures lifts degeneracies, spreads the excitonic spectrum, and closes the bright-dim gap. In fact, we find that the competition between oscillator strength and thermal depopulation only produces non-monotonicity for the low symmetry structures where the bright-dim gap is sufficiently small to compete with the size-dependent oscillator strength increase. We underscore this analysis by constructing a model fit of the size dependent optoelectronic properties. Size-dependent energies and oscillator strengths of excitons in cubic, relaxed, and orthorhombic nanocrystals with 2.5–5.7 nm edge lengths were fitted, and these fitted properties were used to compute the radiative lifetimes (Supplementary Figs. S9–S11). For emphasis, the radiative lifetimes were not fitted. Excitonic states in the BSE framework were calculated for two additional nanocrystals sizes of 6.3 and 6.9 nm (up to 7400 atoms), representing a substantial software development and computational effort due to our inclusion of full spinors, spin-orbit coupling, and open boundary conditions. We capture the non-monotonic turnaround in these test points for both relaxed and orthorhombic geometries, demonstrating that our model is consistent to extrapolate to larger sizes (Fig. 5a). Convergence of the final orthorhombic point proved numerically challenging but is included for completeness. Taking these data together, the interplay of size, symmetry, and excitonic structure manifests a dramatic non-monotonicity in lead halide perovskite nanocrystal radiative lifetimes, revealing that CsPbX3 nanocrystals nearing intermediate confinement show optimal features for applications where rapid photon emission is desirable.
In conclusion, the investigation of the effect of CsPbBr3 nanocrystal size on radiative lifetime at ambient temperature reveals an unexpected non-monotonic trend. Larger and smaller nanocrystals in the weak and strong quantum confinement regimes displayed longer radiative lifetimes, leaving the intermediately confined nanocrystals to exhibit the shortest radiative lifetimes. Interestingly, we observed a structural symmetry-lowering transition from cubic to orthorhombic symmetry that was supported by X-ray diffraction and MD simulations. The structural transition onset occurs for very small cubic nanocrystals with edge lengths around 2 nm and progresses to the lower symmetry orthorhombic phase as nanocrystal size increases. Simulations of excitons with an atomistic pseudopotential + BSE model revealed that large nanocrystals approaching the weak confinement regime showed extended radiative lifetime due to the thermal population at room temperature of high-lying states with weak oscillator strengths. In contrast, the unexpected lengthening of radiative lifetime in smaller nanocrystals within the strong confined regime was attributed to a significant reduction in oscillator strength, leaving the intermediately confined nanocrystals to exhibit the shortest radiative lifetimes. The observed non-monotonic radiative behavior emerges in orthorhombic and relaxed nanocrystals of lowered structural symmetry due to exciton level splitting that reduces the energy gap from the bright to dim states (bright-dim gap) and increases the density of the lower energy dim states; cubic nanocrystals are not predicted to show non-monotonic radiative lifetimes. This optoelectronic behavior lends additional support to the XRD measurements and MD simulations, all suggesting that larger perovskite nanocrystals adopt lower symmetry structures. This study emphasizes the intricate and unique interplay between the CsPbBr3 nanocrystal size and radiative lifetime, paving the way to improve and engineer optical materials with desirable radiative lifetimes for diverse optical applications.