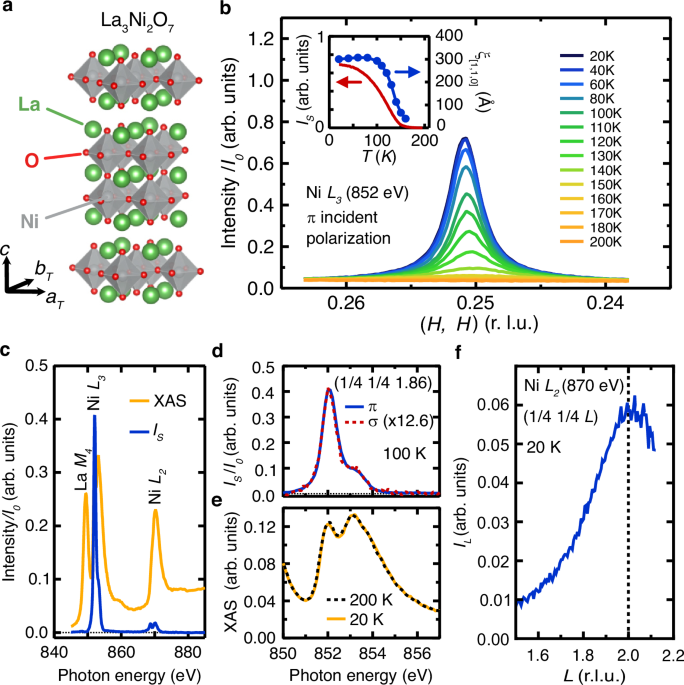
In Fig. 1b, we show RSXS measurements on the Ni L3 edge in π-polarization along the (H, H, 1.86) direction for a series of temperatures. Here, we employ the pseudo-tetragonal unit cell such at aT and bT parallel to the in-plane NiO bond directions. Below 160 K, a sharp peak emerges with \({{{\bf{Q}}}}_{{{\rm{SDW}}}}(20\,{{\rm{K}}})\) = \(\left(0.2508,\,0.2508,L\right)\), slightly incommensurate, but within experimental accuracy of the commensurate value \(\left(\frac{1}{4},\frac{1}{4},L\right)\). The peak intensity is approximately 45 times stronger in π versus σ polarization at 20 K, suggesting that the scattering originates from magnetic rather than charge ordering, consistent with previous measurements4. The resonance energy dependence of the high-temperature background subtracted scattering intensity, \({I}_{s}\left({{\hslash }}\omega,100{{\rm{K}}}\right)=I\left({{\hslash }}\omega,100{{\rm{K}}}\right)-I\left({{\hslash }}\omega,220\,{{\rm{K}}}\right)\), at the SDW peak maximum for L = 1.86 is shown in Fig. 1c, together with the x-ray absorption spectrum (XAS). This demonstrates that the \(\left(\frac{1}{4},\frac{1}{4}\right)\) Bragg peak is peaked only at the Ni L resonances, and not on the La M4 edge or off-resonance.
Fig. 1: Magnetic Resonant Scattering and X-Ray Absorption of La3Ni2O7.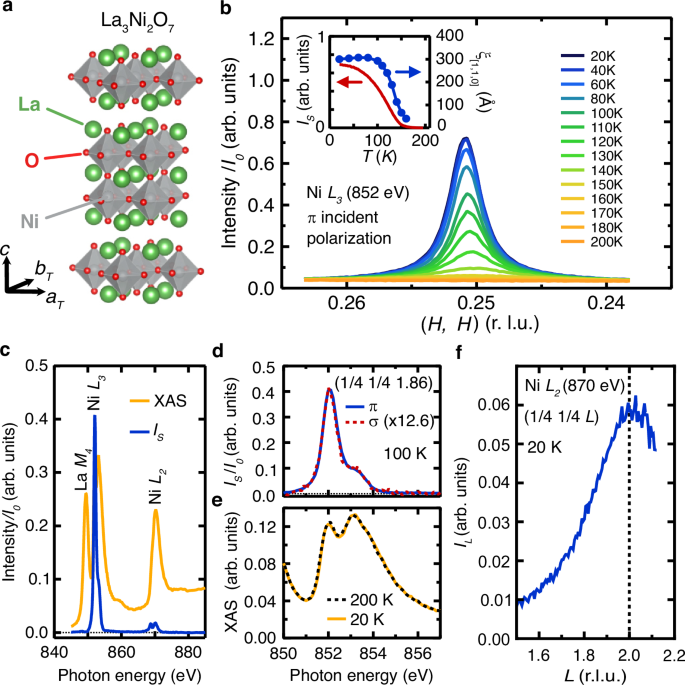
a The crystal structure of La3Ni2O7, with the pseudo tetragonal axes aT and bT denoting the in-plane NiO bond directions. b The intensity (scattering + background) for cuts along the (H, H, 1.86) direction through the SDW peak at various temperatures, measured at the Ni L3 absorption edge with π incident polarization for sample A. Inset: The SDW peak amplitude, \({I}_{s}(T)=I\left(T\right)-I\left(220{K}\right)\) (red), and correlation length along the [1 1 0] direction (blue) as a function of temperature. c The energy dependence of the SDW peak amplitude, \({I}_{s}\left(\hslash \omega,100{K}\right)=I\left(\hslash \omega,100{K}\right)-I\left(\hslash \omega,220{K}\right),\) measured with π incident light at L = 1.86 through the Ni L and La M edges (blue), along with the x-ray absorption (XAS) measured via partial fluorescence yield (orange). The scattering is peaked at the Ni L resonances but is absent off resonance or at the La M4 resonance. d The energy dependence of the SDW peak amplitude at 100 K and L = 1.86 at the Ni L3 edge with σ and π incident light. e The Ni L3 x-ray absorption measured using partial fluorescence yield (PFY) at base temperature (20 K) and above the SDW phase transition (200 K). f The L dependence of the SDW structure factor, IL, at 20 K of the SDW peak at the Ni L2 edge (870 eV) for sample B.
In Fig. 1f, we show the L dependence of the SDW structure factor, IL, at the in-plane \(\left(\frac{1}{4},\frac{1}{4}\right)\) wavevector on the Ni L2 edge (870 eV). Note, the L2 edge is chosen for this purpose for its higher energy and thus a larger accessible range of L relative to the Ni L3 edge. While the scattering intensity \({I}_{S}(L)\) is peaked at an incommensurate L value (see Supplementary Information Section VI), assessing the L dependence of the SDW structure factor, \({I}_{L}\), requires correction for the variation in the measurement geometry during the L scan to account for both the absorption of the incident and scattered x-rays and the projection photon polarization onto the crystallographic axes. These corrections are akin to the well-known polarization and absorption corrections of conventional x-ray diffraction but are generalized for absorption from a thin film and for resonant scattering from the in-plane magnetic structure identified below (see Supplementary Information Section VI). As shown in Fig. 1f, \({I}_{L}\) is peaked at L = 2, but with only a 14 ± 4 \({{\text{\AA}}}\) correlation length along the c – direction, revealing the highly two-dimensional nature of the magnetic order in La3Ni2O7.
We note that both the resonance energy and L dependence of \(\left(\frac{1}{4},\frac{1}{4}\right)\) SDW Bragg peak establish that the SDW intrinsically originates from La3Ni2O7 and not an impurity phase, as has plagued the identification of ostensible charge or spin density order in other related nickelates16,17. Specifically, the energy dependence of the scattering is consistent with magnetic order, with a similar energy dependence to other magnetically ordered nickelates18,19,20, and is inconsistent with a structural superlattice, such as staged oxygen impurities. The L dependence peaked at an integer L value, indicates the SDW order corresponds to the c-axis lattice constant of La3Ni2O7 as opposed to other magnetically ordered compounds such as RENiO318,19,20 or La2Ni2O521 that also exhibit (1/4, 1/4, L) magnetic order but have different lattice constants and/or order peaked at non-integer values of L.
In many related nickelates in the Ruddlesden-Popper sequence, including n = 1 La2−xSrxNiO4 and n = ∞ perovskite RENiO3 (RE = Nd, Pr, Sm), SDW order coincides with strong charge or bond disproportionation, where the local electronic and orbital environment of the Ni sites is strongly modulated at an atomic scale18,19,22,23,24,25,26,27. Whether such behavior also occurs in La3Ni2O7 remains an important open question. Evidence of charge order or bond disproportionation can be most directly identified from the observation of structural changes and superlattice charge peaks. In addition, charge order may exhibit anomalies in transport and thermodynamic properties, such as the metal-insulator transition that is tied to charge disproportionation in RENiO324,25, semiconductor-insulator transitions tied to spin-charge order in La2−xSrxNiO422 or La4Ni3O828,29, or the metal-metal transition tied to spin-charge order in La4Ni3O1030. In cuprate superconductors, charge order can also be evident in a change in the Hall and Seebeck coefficients, indicative of Fermi surface reconstruction with the onset of CDW order31.
Evidence of bond disproportionation in RENiO3 is also found in resonant x-ray diffraction and x-ray absorption spectroscopy. In RENiO3, the onset of bond disproportionation leads to spectroscopically distinct Ni sites that can be identified as temperature-dependent changes in the XAS across the metal-insulator transition32,33,34. With resonant x-ray scattering, signatures of bond disproportionation can be detected in the energy and polarization dependence of the resonant scattering. Ni sites having a different orbital occupation and local crystal field, such as long-bond and short-bond Ni sites in RENiO3, will modulate the x-ray scattering form factors on the different Ni sites, leading them to resonate at slightly different energies35. These distinct Ni sites also exhibit a different magnitude and orientation of the spin. As the scattering intensity depends on the orientation of the x-ray polarization with respect to the spin, Ni sites with distinct charge environments can result in the linear dichroism of the SDW peak intensity (σ versus π incident polarization) becoming energy dependent (see Supplementary Information Section III), as reported in RENiO3 heterostructures18.
Considering these signatures of charge order, we find no evidence for charge order or charge disproportionation in our samples of La3Ni2O7. We observe no distinct changes in the Ni L edge XAS spectra across TSDW (Fig. 1e), and the linear dichroism of the \(\left(\frac{1}{4},\frac{1}{4}\right)\) peak in La3Ni2O7 does not exhibit any observable energy dependence (Fig. 1d), suggesting that all Ni sites have the same orbital occupation and magnitude of spin in the SDW state. In addition, we do not detect strong anomalies in either the resistivity or Hall coefficient (See Supplementary Information Supplementary Fig. S1), nor do we identify evidence of structural phase transitions or superlattice peaks from hard x-ray diffraction (See Supplementary Information section II). While these measurements collectively constitute a null result, they suggest that the dominant order parameter is magnetic and that, unlike many other nickelates, any associated charge modulation in our samples is either absent, does not onset near TSDW or is too weak to be detected in our present measurements.
Measurement of spin configuration
We now determine the orientation of the staggered moments at 20 K, deep within the SDW state. For this, we make use of the sensitivity of the intensity of resonant scattering to the orientation of the photon polarization relative to the magnetic moments, analogous to polarized neutron scattering18,26,35,36. The resonant elastic x-ray scattering cross-section is given by refs. 35,37:
$${I}^{{\mathrm{cr}}}\left({{\boldsymbol{\epsilon }}}_{{\mathrm{in}}},{{\hslash }}\omega,{{\bf{Q}}}\right)\propto {\left|{{\boldsymbol{\epsilon }}}_{{\mathrm{out}}}^{*}\cdot \left({\sum}_{j}{F}_{j}\left({{\hslash }}\omega,{{\bf{Q}}}\right){e}^{i{{\bf{Q}}}\cdot {{{\bf{r}}}}_{j}}\right)\cdot {{\boldsymbol{\epsilon }}}_{{\mathrm{in}}}\right|}^{2}$$
(1)
where \(\hslash \omega\) is the photon energy, \({{\bf{Q}}}={{{\bf{k}}}}_{{\mathrm{out}}}-{{{\bf{k}}}}_{{\mathrm{in}}}\) is the momentum transfer and \({{{\boldsymbol{\epsilon }}}}_{{{\rm{in}}}}\) and \({{{\boldsymbol{\epsilon }}}}_{{{\rm{out}}}}\) are the incident and scattered x-ray polarization, respectively. Fj is a tensor that encodes the photon energy dependence of the scattering cross-section for site j in the lattice, and its elements depend on the orientation of the magnetic moment at site j35. (see Supplementary Information section III) Assuming spherical symmetry of the local valence charge density, consistent with the linear dichroism of the SDW peak being energy-independent (Fig. 1d), the scattering depends on the orientation of the staggered \(\Delta {\bf{m}}\) as
$${\sum}_{j}{F}_{j}\left({{\hslash }}\omega ,{{\bf{Q}}}\right){e}^{i{{\bf{Q}}}\cdot {{{\bf{r}}}}_{j}}\propto \left[\begin{array}{ccc}0 & {\Delta {{\rm{m}}}}_{\left[001\right]} & -{\Delta {{\rm{m}}}}_{\left[110\right]}\\ {-\Delta {{\rm{m}}}}_{\left[001\right]} & 0 & {\Delta {{\rm{m}}}}_{\left[-110\right]}\\ {\Delta {{\rm{m}}}}_{\left[110\right]} & -{\Delta {{\rm{m}}}}_{\left[-110\right]} & 0\end{array}\right],$$
(2)
where ∆mu are the components of the staggered moments in three orthogonal directions [001], [− 110] and [110].
These components can then be deduced by varying the alignment of ϵin relative to the [001], [− 110] and [110] directions. In an experiment, this is achieved by rotating the sample azimuthally by an angle ϕ about an axis normal to the \(\left[\frac{1}{4},\frac{1}{4},L\right]\) set of lattice planes (here L is 1.93), as depicted in Fig. 2a, which is accomplished by mounting the c-axis normal film on a 43.7° wedge. This approach enables the orientation of the moments to be rotated relative to the incident polarization, which can be set to be π, σ, circular or linear 45° (π − σ), with the scattering wavevector remaining centered on the \(\left(1/4,\,1/4,\,1.93\right)\) peak. As shown in Fig. 2b, the scattering intensity, measured here at 20 K, has a strong dependence on the azimuthal angle, ϕ as well as on the polarization of the incident light. In Fig. 2c, we plot the SDW peak amplitude as a function of azimuthal angle ϕ, for our various incident polarizations. Notably, the peak intensity exhibits a complex, non-monotonic dependence with ϕ and large variations with incident polarization. This azimuthal dependence can be compared to simulations of the staggered moments oriented along different directions, calculated using Eqs. 1 and 2, the sample geometry, and a correction for the geometry-dependent absorption of the incident and scattered x-rays (Supplementary Information Section IIIB). As shown in Fig. 2c the measurements show remarkable agreement with the moments forming diagonal, bicollinear spin stripes (Fig. 2d) with the magnetic moments lying entirely within the a − b plane but oriented perpendicular to \({{{\bf{Q}}}}_{{\mathrm{SDW}}}\). We emphasize this model was calculated without any free-fitting parameters, apart from an overall scaling factor.
Fig. 2: Measuring Orientation of Magnetic Moments.
a The measurement geometry for azimuthal angle (ϕ) dependent measurements. The sample is mounted on a 43.7 deg wedge to align the \(\left[\frac{1}{4},\frac{1}{4},1.93\right]\) set of planes with the azimuthal rotation axis. The incident photon polarization is set to be σ, π, linear 45° (π − σ) or circular. The sample was rocked about the vertical axis by angle θ to measure the intensity and width of the \(\left(\frac{1}{4},\frac{1}{4},1.93\right)\) SDW peak. b The scattering intensity, \({I}_{s}=I\left(T\right)-I\left(200{K}\right)\), versus θ through the SDW peak at ϕ values between 0 and 180 degrees for π, σ, circular and linear 45° incident x-ray polarization at 20 K. The scattering intensity, IS, is found by subtracting the background fluorescence measured above TSDW (200 K) from the total intensity (scattering + background fluorescence) measured at 20 K. c The SDW peak amplitude, IS, at 20 K versus ϕ for π, σ, circular and linear 45° incident polarization. Solid lines are the ϕ dependence calculated for a magnetic structure with \(\Delta {{\bf{m}}}\) parallel to [−110], depicted in (d). e The 3D magnetic unit cell is deduced from the azimuthal angle dependence and assuming anti-ferromagnetic bilayer coupling. f The ϕ and polarization dependence that would result from the spin configurations depicted in (g).
In contrast, the calculated polarization and ϕ dependence for other possible SDW scenarios (Fig. 2f, g), including \(\Delta {{\bf{m}}}\) out of the plane, \(\Delta {{\bf{m}}} \parallel {{{\bf{Q}}}}_{{\mathrm{SDW}}}\), or a non-collinear configuration, all bear no qualitative resemblance to the experimental data (Fig. 2c), indicating the relative contribution of \(\Delta {{\bf{m}}}\) out of the NiO plane or parallel to \({{{\bf{Q}}}}_{{\mathrm{SDW}}}\) is less than a few percent at 20 K.
Having constrained the orientation of moments predominantly within the NiO2 planes, we can now consider the full 3D magnetic structure, which is informed by the L dependence of the SDW scattering cross-section. The fact that the SDW order is peaked at L = 2 and is minimal at L = 1.5, (Fig. 1f) indicates that with the coupling within the bilayer (intra-bilayer coupling) and between bilayers (inter-bilayer coupling) are either both ferromagnetic or both antiferromagnetic (see Supplemental Information Section VI). Given that the reasonably straight interlayer Ni-O-Ni bond is likely to involve antiferromagnetic super-exchange and that the experimental magnon dispersion is well described by a model with a large AF bilayer coupling2, this suggests the magnetic structure is consistent with the one depicted in Fig. 2e, with both inter- and intra-bilayer AF coupling.
This bicollinear double spin-stripe configuration is notably different from many other nickelates, including the non-collinear spin-spiral magnetic order in thin films of RENiO318,19,20, the collinear order with moments parallel to \(\left(\frac{1}{4},\frac{1}{4},\frac{1}{4}\right)\) in ultrathin RENiO318, spin/charge stripes with moments perpendicular to the planes in the square-planar trilayer nickelate La4Ni3O829, the reported magnetic order, with moments along c, in La2Ni2O523, and spin-stripe order in La2-xSrxNiO438,39, which has staggered moments oriented within the NiO planes but not perpendicular to \({{{\bf{Q}}}}_{{\mathrm{SDW}}}\). Staggered moments in the NiO planes and perpendicular to \({{{\bf{Q}}}}_{{\mathrm{SDW}}}\) are found in both single-layer La2NiO4+δ 27 and the trilayer La4Ni3O1030,40, suggesting a potential link between the SDW in these compounds and La3Ni2O7. However, these compounds both exhibit spin-charge stripe order, with La2NiO4+δ being an insulator and La4Ni3O10 having incommensurate spin-charge stripe order. In both wavevector and orientation of moments, the SDW order in La3Ni2O7 is also similar to the bicollinear double spin stripe observed in FeTe41,42,43.
Anisotropic, unidirectional magnetic domains
The unidirectional, stripe-like character of the antiferromagnetic order is also manifest in the shape of the SDW domains, which break the rotational symmetry of the lattice. We measured the shapes and intensities of the SDW Bragg peaks in the H − K plane for both sets of SDW domains with orthogonal \({{\bf{Q}}}\) vectors, around \(\left(\frac{1}{4},\frac{1}{4},L\right)\) (in red) and \(\left(\frac{1}{4},-\frac{1}{4},L\right)\) (in blue) using a two-dimensional microchannel plate detector, shown in Fig. 3a. The Bragg peaks around \(\left(\frac{1}{4},\frac{1}{4},L\right)\) and \(\left(\frac{1}{4},-\frac{1}{4},L\right)\) have equal intensities to within experimental uncertainty ( ± 3 %), indicating an equal population of domains. In both sets of domains, the SDW peaks have highly anisotropic shapes, with a 2D Lorentzian fit giving correlation lengths that are much longer parallel to QSDW (ξ|| = 292 Å) versus perpendicular to \({{{\bf{Q}}}}_{{{\rm{SDW}}}}\) (ξ⊥ = 134 Å).
Fig. 3: Anisotropic Bragg peaks indicative of stripe-like SDW domains.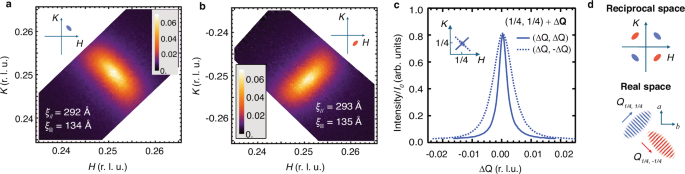
The shape of the (a) (1/4 1/4 L) and (b) (1/4 -1/4 L) Bragg peaks at 852 eV with π incident polarization. Measurement of H and K for sample A using a 2D channelplate detector (integrated between L = 1.81 and 1.90). The orthogonal peaks have the same intensities and widths. c Cuts through the (1/4 1/4 1.85) Bragg peak parallel and perpendicular to the in-plane Q vector. d The shape of Bragg peaks in reciprocal space and the corresponding domain structure in real space for anisotropic domains of unidirectional stripe order, consistent with the measurements in (a) and (b).
This peak shape is consistent with anisotropic domains of unidirectional SDW order, with each domain characterized by either (1/4, 1/4) or (-1/4, 1/4) order, as depicted in Fig. 3d. This anisotropy could be associated with orthorhombic structural twin domains or maybe orthogonal domains of unidirectional order occurring within a single structural domain. Intriguingly, this latter scenario is reminiscent of the anisotropic charge ordering reported in underdoped YBa2Cu3O7−δ and Bi2Sr2−xLaxCuO6+δ, where the CDW Bragg peaks likewise exhibit an anisotropy, with longer correlations lengths parallel to the CDW wavevector, indicative of orthogonal anisotropic unidirectional CDW domains within a single orthorhombic structural domain44,45.
Probing magnetic domain walls
In Fig. 2, the orientation of the staggered moment at 20 K was determined to be almost entirely within the a − b plane and perpendicular to \({{{\bf{Q}}}}_{{\mathrm{SDW}}}\) (i.e., \(\Delta {{\bf{m}}} \, \parallel \left[-{\mathrm{1,1,0}}\right]\) for \({{{\bf{Q}}}}_{{\mathrm{SDW}}}\) = (1/4, 1/4, L) domains or \(\Delta {{\bf{m}}}\parallel \left[{\mathrm{1,1,0}}\right]\) for \({{{\bf{Q}}}}_{{\mathrm{SDW}}}\) = (− 1/4, 1/4, L) domains). Insights may be gleaned from the small discrepancies between the model and measurements. In particular, measurements using σ polarization at ϕ = 0 are at a minimum in intensity for this magnetic orientation, with deviations of the staggered moment in the NiO planes, but parallel to \({{{\bf{Q}}}}_{{{\rm{SDW}}}}\) and/or along [001] required to provide a finite scattering intensity. We now leverage this sensitivity of the polarization to the staggered moment orientation to investigate how the spin configuration evolves with temperature. In Fig. 4b, we show a comparison between the temperature dependence of the SDW peak when measured with π versus σ polarization. At low temperatures (T K), the scattering intensity of the SDW peak measured in π polarization, Iπ, is more than an order of magnitude stronger than in σ polarization, Iσ. Upon raising the temperature to TSDW, Iπ, smoothly decreases whereas Iσ exhibits a non-monotonic temperature dependence, growing in intensity before peaking around 130 K, and then falling rapidly to zero at TSDW. On the other hand, the ratio of Iσ /Iπ, shown in Fig. 4c grows smoothly and monotonically with increasing temperature all the way up to TSDW when the peak vanishes, indicating that the component of the spins oriented away from the low T configuration (Fig. 2c) grows with increasing temperature, with Iσ/Iπ > 0.6 near TSDW.
Fig. 4: Temperature dependence of (1/4 1/4 L) Bragg peak with σ photon polarization.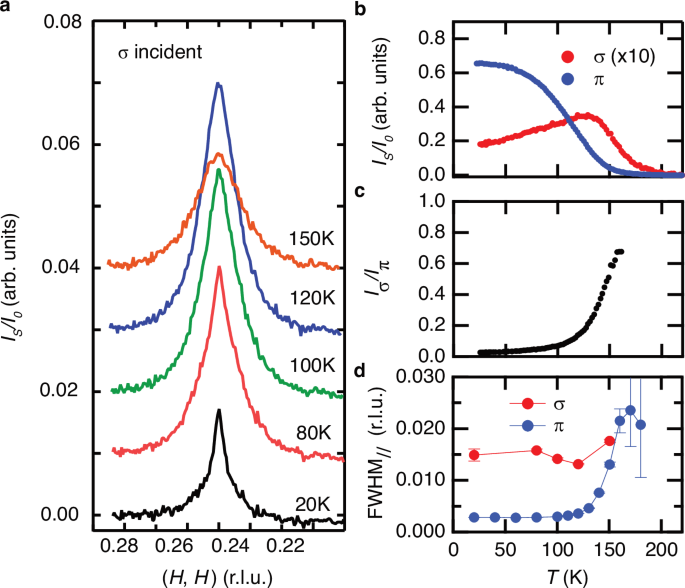
a Cuts of the scattering intensity through the SDW peak at L = 1.93 and 852 eV with incident σ photon polarization at various temperatures. The peak is broader with σ polarization than with π polarization (Fig. 1b) and exhibits a non-monotonic temperature dependence. b The temperature dependence of the (1/4 1/4 1.93) peak amplitude, \({I}_{s}\), with σ and π incident polarization. The peak emerges at 200 K, but peaks at 130 K with σ polarization. c The ratio of the scattering intensity from σ and π incident light, \({I}_{\sigma }/{I}_{\pi }\), which increases monotonically with increasing temperature. d The FWHM of the (1/4 1/4) peak with σ and π incident light. As described in supplementary section VII, IS with σ incident light is fit to two peaks (broad and narrow). The narrow peak has FWHM comparable to the IS with \(\pi\) incident light and is evident at 20 K in a) but diminished above 100 K. We attribute the narrow peak to an artifact of a few percent contribution of \(\pi\) incident light in the nominal σ polarized beam. The FWHM of the remaining broad peak is shown in d).
In addition to this anomalous temperature dependence, the width of the SDW Bragg peak is surprisingly broader when measured with σ versus π incident polarization (Fig. 4a, d) Note, in Fig. 4d the peak width with σ polarization is deduced by subtracting a narrow peak resulting from ~ 1.5% π incident light in the nominally σ polarized beam, as discussed in Supplementary Information Section VII. The broader peak with σ incident polarization indicates that the staggered moments parallel to \({{{\bf{Q}}}}_{{\mathrm{SDW}}}\) or along [001] (probed with σ incident light) have a shorter correlation length at low temperatures than the predominant spin configuration with staggered moments in the NiO plane and perpendicular to \({{{\bf{Q}}}}_{{\mathrm{SDW}}}\). This observation would be inconsistent with a uniform, temperature-dependent canting of all the spins. Instead, this could be consistent with the existence of real-space defects of the magnetic order, such as Bloch-like domain walls or antiferromagnetic skyrmion-like topological defects. Indeed, Bloch-like domain walls may naturally exist between two orthogonal unidirectional domains, where the transition between domains would necessitate a reorientation of the spins by 90° from one domain to its orthogonal counterpart, which could occur over an extended region, depending on the relative magnitude of the magnetic anisotropy and exchange terms.
In our interpretation of the data in terms of Bloch domain walls, the staggered moments would rotate away from [110] or [− 110] and out of the a − b plane, as depicted conceptually in Fig. 5. Here, \({I}_{\pi }\) would probe the bicollinear spin stripe regions within the core of each domain, while \({I}_{\sigma }\) would be sensitive to the rotated spin component in the domain walls. The relative volume fraction of domain walls would grow with increasing temperature until SDW order is lost at TSDW. This interpretation could explain the broader peak for \({I}_{\sigma }\) when compared to \({I}_{\pi }\), as shown in Fig. 4d. Finally, the influence of the domain walls may also be the source of the small deviations from a perfectly in-plane moment at 20 K depicted in Fig. 2c. This analysis represents a possible new approach to detecting defects in antiferromagnetic order. Unlike ferromagnetic domain walls, antiferromagnetic domain walls are often difficult to detect46. Further analysis of the polarization and temperature dependence of the (1/4 1/4) SDW peaks in La3Ni2O7 may provide key insights into the width, density and detailed magnetic configuration of the domain walls. Such investigations may be of key importance as the magnetic configuration close to TSDW, including a high density of domain walls, may represent the melting of long-range SDW order as the material approaches its superconducting phase.
Fig. 5: Conceptual representation of a magnetic domain wall between Q(110) and between Q(-110) SDW domains.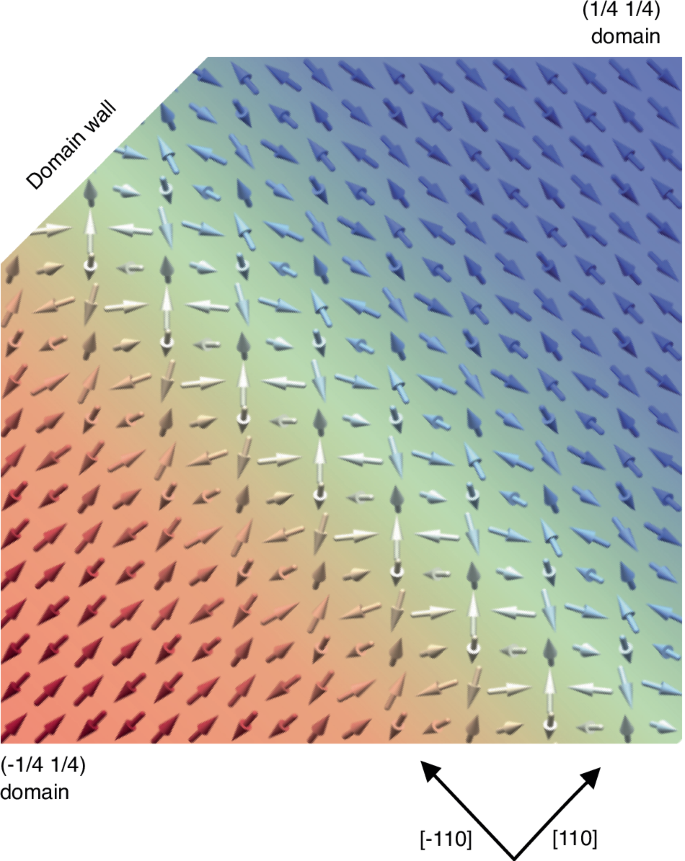
In the vicinity of a domain wall, the spin orientation may rotate to have a sizeable, staggered moment out of the plane and/or parallel to Q.