Connecting theory and experiment
While spin-1/2 chains in magnetic crystals have been studied in the past31,32,33,34, to our knowledge the important question of what happens to spinon excitations at temperatures high compared to the exchange coupling energy scale remains experimentally unexplored. This is largely because the exchange energy scales in most studied spin-chain materials are in the range of tens to hundreds of meV ( J/kB ~ 100 − 1000 K, kB is Boltzmann constant), making it difficult to access temperatures truly in excess of the interaction energies—for example, in KCuF3, J/kB ≈ 400 K, well above room temperature33. From this perspective, YbAlO3 is an ideal material to study because of the relatively weak exchange interaction in its effective spin-1/2 Hamiltonian ( J ≈ 0.21 meV, J/kB ≈ 2.4 K21,22) and the absence of magnetic order down to a temperature of 0.8 K. As a result, we can use inelastic neutron spectroscopy to probe the physics of the Heisenberg spin-1/2 chain in a temperature regime that is unattainable in other spin-1/2 chain materials.
The spin-1/2 Heisenberg Hamiltonian is a well-established low-energy effective description of a Mott-insulating Hubbard chain at half-filling35,36,37,38. In YbAlO3, a transparent insulator with an optical gap of approximately 5 eV, the Yb3+ ions form chains characterized by an estimated Hubbard interaction U ~ 20 eV and hopping amplitude t ~ 50 meV35,39. These parameters yield an exchange coupling J ~ 4t2/U ~ 0.5 meV, which is roughly consistent with experiment and supports the validity of the low-energy spin-1/2 model38. The temperature range explored in this work lies well below the regime37 where the charge sector above the Mott gap becomes relevant. The effective spin-1/2 Hamiltonian, accounting for the large orbital degeneracy of the Yb J = 7/2 multiplet in this parameter range, was rigorously derived from the one-dimensional Hubbard model in ref. 36. The crystal-field splitting between the ground and first excited doublets of the Yb multiplet, estimated to be ~ 20–30 meV21, thus represents the lowest atomic energy scale that can compromise the spin-1/2 description at elevated temperatures.
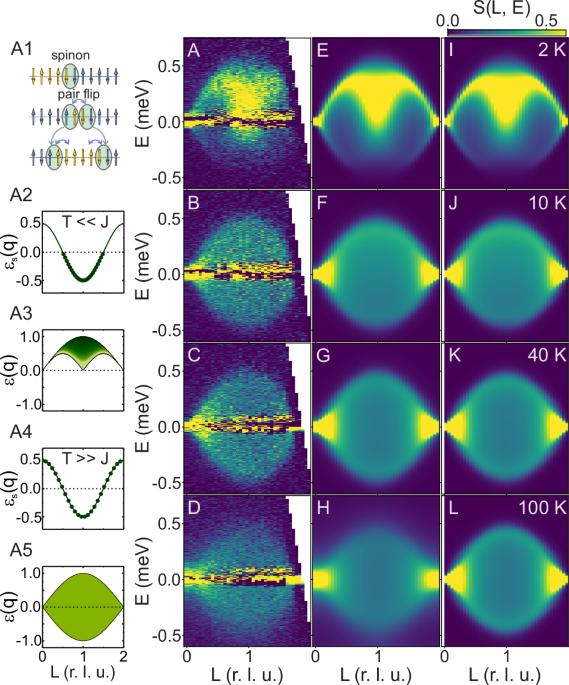
Here, we report a detailed INS investigation of the spinon spectrum in YbAlO3 as a function of temperature in the 2 − 100 K (~(1 − 40) × J) range. The excitation spectrum of the ideal spin-1/2 Heisenberg chain is known to consist of pairs of spinons, fractional elementary excitations each carrying S = 1/2 angular momentum3,4. Pair-states of these spinon excitations encode physical spin flips in the chain [this is schematically illustrated in Fig. 1(A1)], whose energy spectrum forms a continuum, at zero-temperature sharply bounded by the two-spinon boundaries (q is the wave vector, d is the lattice spacing)31,32,33,34,40,
$$\frac{\pi }{2}J| \sin qd| \le \epsilon (q)\le \pi J\left\vert \sin \left(\frac{qd}{2}\right)\right\vert$$
(1)
Qualitatively, the lower and upper two-spinon continuum boundaries show different behavior as a function of temperature, which can be understood by considering spinons as fermion quasiparticles half-filling the one-dimensional energy band, \({\epsilon }_{s}(q)=\frac{\pi }{2}J\sin qd\)23,41 (See Supplementary Information for details of data and theoretical analysis and DMRG calculations.). The lower continuum boundary arises because of the complete occupation of states below the spinon Fermi energy at zero temperature, which forbids excitations into the filled states [Fig. 1(A2,A3)]. With the increasing temperature, the Fermi distribution smears out, allowing state occupations above the Fermi level at the expense of the occupied states below it [Fig. 1(A4)]. As a result, the lower boundary blurs until it completely disappears at temperatures \(\gtrsim \frac{\pi }{2}J/{k}_{B}\). On the other hand, the upper boundary reflects the maximum energy that a spinon pair with a given q can have according to the dispersion, ϵs(q). In the absence of spinon decoherence through a finite collisional lifetime in the idealized system described by the quantum spin-chain Hamiltonian, the profile of the upper two-spinon boundary must remain completely untouched by temperature effects [Fig. 1(A5)]. The upper boundary of the excitation continuum is only blurred beyond the two-spinon boundary by the presence of multi-spinon-excitations. At T = 0, the total spectral weight above this upper boundary from such excitations is relatively small (~ 1%)40. While this blurring is in fact temperature-dependent, it is entirely governed by the quantum spin Hamiltonian and as our theoretical calculations show remains insignificant even at high temperatures, T ≫ J/kB.
Effects of finite lifetime on spinon spectra
In the presence of couplings to a system external to the quantum spin Hamiltonian, such as a thermal heat bath or other extrinsic source of decoherence, a quantum spin-chain will experience information loss to these external degrees of freedom. This will be reflected by a reduced spinon lifetime, measurable in neutron spectra by a broadening along the energy direction beyond instrument resolution. A blurring of the upper boundary of the excitation continuum in excess of the theoretically calculated width generated by multi-spinon excitations is then a metric for spinon decoherence, quantifying the degree of information loss from the spin-chain to the environment.
Theoretically, the sharp upper boundary of the two-spinon continuum in the dynamical structure factor, as measured by inelastic neutron scattering, is determined by the step-like behavior arising from the integration of a delta function that enforces energy conservation over the internal momentum of the two-spinon states40,42,43,44,45,46,47. Equivalently, this corresponds to integrating single-particle Green’s functions within the two-particle susceptibility (see the discussion in Supplementary Information Section II E for the case of the Jordan-Wigner fermion representation). When spinon eigenstates acquire a finite lifetime τ, the delta function transforms into a Lorentzian profile with half-width Γ = ℏ/τ. This transformation is mathematically represented as a convolution of the original expression with a Lorentzian function of half-width Γ. Assuming that the lifetime τ is wave-vector independent—an assumption justified a posteriori by comparison with experiment—this convolution can be moved outside the integration over the internal momentum of the spinon pair and applied directly to the dynamical structure factor of an ideal chain, thereby modifying the previously calculated sharp two-spinon boundary to reflect finite-lifetime effects.
While our treatment of the finite lifetime of unbound two-spinon states is phenomenological, a comparison with the experimental results presented below demonstrates that it adequately captures the essential physics of spinon decoherence. The analysis shows that decoherence arises from the thermal activation of a crystal-field doublet whose energy is approximately two orders of magnitude larger than that of the spinon dispersion, providing strong physical justification for neglecting the wave-vector dependence of the lifetime. Finally, we note that in extracting the finite spinon lifetime, we rely on comparison with state-of-the-art DMRG calculations, which are widely recognized as one of the most accurate numerical methods for one-dimensional quantum spin systems, particularly the spin-1/2 Heisenberg chain, where it has been extensively benchmarked against exact solutions from the Bethe ansatz48,49.
Analysis of spinon spectra with finite lifetime
Figure 1 shows the temperature dependence of the measured spinon continuum in YbAlO3 side-by-side with temperature-dependent realizations of the spin-1/2 Heisenberg model from finite-temperature DMRG calculations (see “Methods”). The left column shows our experimentally measured dynamical structure factors, normalized to absolute units as described in the Supplementary Information. The middle column shows a fit of our DMRG-calculated spectra to the experimental data, including convolution with the known instrumental resolution function and a Lorentzian broadening function with half-width Γ to model finite spinon life-time, τ = ℏ/Γ24,26. The right column shows the DMRG calculations without the Lorentzian broadening, demonstrating how the spectrum would appear if the effects of spinon thermal decoherence were absent. The waterfall plot in Fig. 2 shows constant-L line-cuts of data and the corresponding Lorentzian-broadened DMRG calculation at selected wave-vectors, which demonstrates the excellent agreement between our model and data (values for the reduced χ2 goodness-of-fit parameter are listed in the caption and are below 3 for all temperatures; L is the component of the wave vector, Q = (H, K, L), along the chain direction, see “Methods”).
Fig. 2: Line cuts along the energy axis of our data and fits to our model.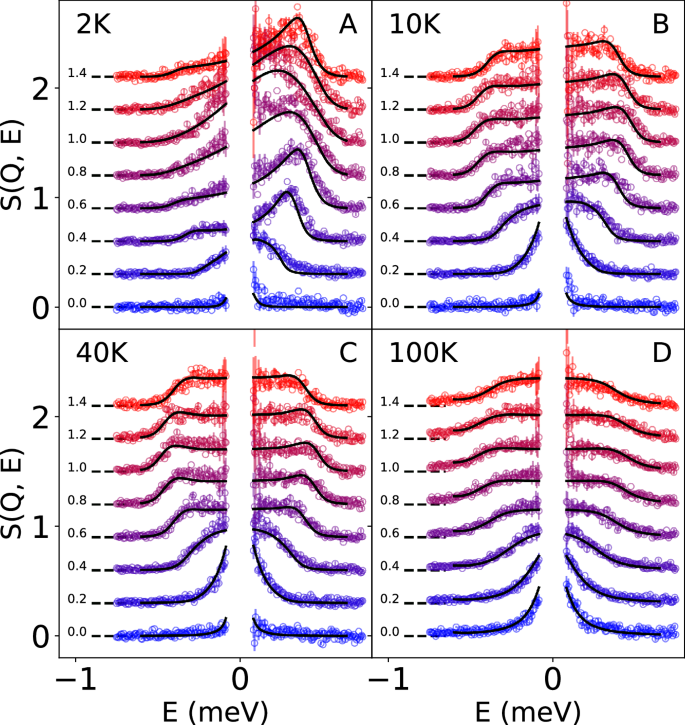
Curves are given an incremental offset for visualization, with dashed leader-lines from each curve signifying the zero of intensity. The labels next to each curve signify the central L value of each line-cut, which are 0.2 r. l. u. wide. A 2 K (r. χ2 = 2.1). B 10 K (r. χ2 = 1.9). C 40 K (r. χ2 = 1.3). D 100 K (r. χ2 = 1.2). Error bars represent one standard deviation (SD).
At 2 K, the lower continuum boundary is visible in both experiment and DMRG simulations, albeit already slightly blurred by thermal repopulation as temperature is comparable to the exchange coupling, J/kB = 2.4 K. At higher temperatures, 10 K and above, all signs of the lower continuum boundary have disappeared in both experiment and simulation [Fig. 1A–D] and instead been replaced by a flat continuum [Fig. 2B–D]. This flat continuum, however, remains clearly bounded by the dispersive upper boundary even at temperatures far higher than the exchange coupling. Remarkably, our experimentally measured datasets demonstrate this clear upper-boundary dispersion at temperatures as high as 100 K, forty times greater than the exchange interactions within the system. Only a slight blurring of the upper boundary can be seen, which is most clearly visible in the 1-dimensional plots in Fig. 2. This blurring appears well modeled by the wave-vector-independent Lorentzian damping, Γ, indicating finite spinon lifetime at high temperatures.
Figure 3A shows Γ as a function of temperature, revealing no measurable spectral broadening beyond resolution at temperatures below 60 K. Above this point, however, the dispersion does become measurably blurred, with Γ eventually reaching an energy-scale of ~ 0.1 meV at 100 K, consistent with thermally activated behavior. An Arrhenius type fit, \(\Gamma (T)={\Gamma }_{0}{e}^{-\frac{Ea}{{k}_{B}T}}\), yields activation energy of Ea ≈ 20 meV. This energy scale is consistent with the thermal population of crystal-field levels other than the ground-state doublet, which invalidates the Seff = 1/2 description of the Yb ions, leading to decoherence and information loss. Slight thermal depletion of the ground-state doublet is also consistent with a subtle reduction in the integrated intensity of the measured spinon continuum above 60 K, visible in the inset of Fig. 3A, though this effect is small (with ≲ 10% of doublets thermally activated at 100 K) and lies at the limit of our experimental accuracy. The onset of this decoherence mechanism would shift to higher temperatures if the first excited crystal-field level were higher in energy and would vanish entirely if its energy were infinite.
Fig. 3: Temperature dependence of INS spectral parameters and quantum Fisher information (FQ).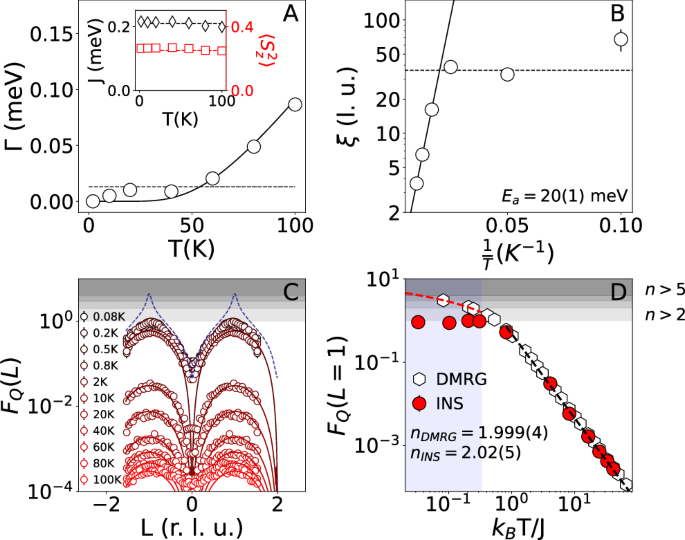
A Life-time broadening parameter as a function of temperature. Dashed line is instrumental resolution HWHM (= 0.013 meV) calculated for E = 0.5 meV. Solid curve is a fit to Arrhenius-type exponential function as described in the text. The inset shows fitted exchange interaction, J, and integrated intensity, \(\langle {S}_{z}^{2}\rangle\), at different temperatures; horizontal lines indicate nominal values, J = 0.21 meV21,22 and \(\langle {S}_{z}^{2}\rangle=1/4\). B Coherence length calculated using the spinon dispersion and extracted lifetime. Solid and dashed lines are asymptotic Arrhenius and resolution-limited behaviors as in (A). C Wave-vector dependence of the QFI, FQ(L), at various temperatures. Dashed curve is an approximation to asymptotic zero-temperature limit calculated from DMRG data at 200 mK as described in the text. D Temperature dependence of maximal quantum Fisher information, FQ(L = 1). Dashed black line is a power-law fit to the data in T ≥ 2 K range capturing asymptotic high-temperature behavior, FQ ~ ( J/T)n, with n = 2. Dashed red curve, shown in the region below TN = 0.8 K (shaded), is a fit of DMRG data below 4 K to a logarithmic dependence, \({F}_{Q}={\left[\ln (aJ/{k}_{B}T)\right]}^{\alpha }\), with J = 0.21 meV and fitting parameters a = 1.55(2) and α = 1.04(1), illustrating the low-T asymptotic behavior; in YbAlO3 it is arrested by static order below TN, where part of the excitation spectrum condenses into elastic Bragg peaks that do not contribute to QFI. Error bars represent one SD and, where not visible, are smaller than the symbol size.
We note that according to the Bethe ansatz, spinons are coherent quasiparticles in the 1D spin-1/2 Heisenberg chain with a well-defined dispersion \(\epsilon (q)=\frac{\pi }{2}J\sin q\)40,42,44,45,46,47,47, which is experimentally revealed through the sharp boundaries of the two-spinon continuum. In our estimate of the coherence length, we use the maximum group velocity derived from this dispersion, which reflects the maximum physical propagation speed of a single spinon excitation. As pointed out by Scheie et al. in ref. 49 and highlighted in Fig. 4 of our manuscript, this velocity is also experimentally revealed through a “light cone” feature in the Fourier-transformed real space-time response function, reflecting the maximum excitation propagation speed in the system, which is directly measurable from neutron scattering data. The coherence length, ξ ~ vτ, thus represents the distance over which a spinon can propagate coherently in the presence of finite-lifetime effects.
Fig. 4: Direct-space and time response functions, χ″(x, t) = − iF [χ″(Q, E)], as a function of temperature.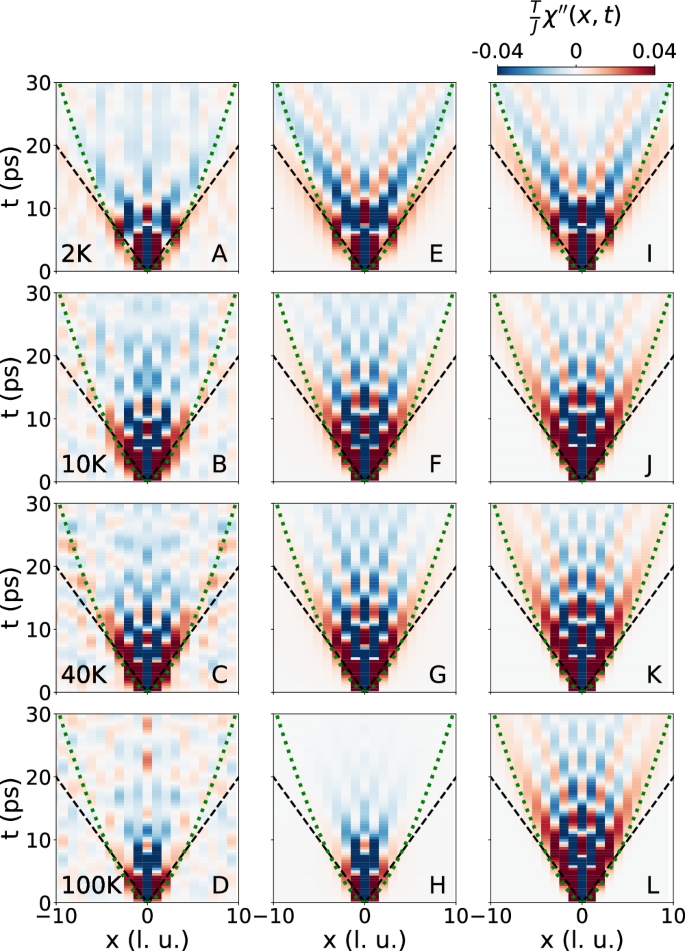
A–D Calculated from inelastic neutron scattering spectra; E–H Calculated from fits to inelastic neutron data; I–L Obtained from DMRG calculations. Dashed black lines mark the edge of the light-cone in the ballistic regime, \(t=\frac{x}{2\pi v}\), while dotted green curves highlight the long-time super-diffusive behavior, t ~ x3/2 54, prominent at high temperatures.
Using the group velocity of spinons from the dispersion near L = 0, v = πJ/2, we can obtain an effective spinon coherence length (mean free path), ξ = vτ = vℏ/Γ, shown in Fig. 3B versus the reciprocal of temperature. When measurable broadening does develop at temperatures above 60 K, the effective coherence length appears to track a decreasing exponential trend with increasing temperature. Fits to an Arrhenius-type model, \(\xi={\xi }_{0}{e}^{\frac{Ea}{{k}_{B}T}}\), where values ξ > ξ0 are replaced by a fitted constant ξ0 ≈ 35 in agreement with our resolution limit, are shown over-plotted on the measured data in Fig. 3B. According to this analysis, the coherence length exceeds 35 lattice units as it passes beyond the resolution limit of our measurements at staggeringly high temperature of 40 K (≈ 17J). The value of Ea ≈ 20 meV obtained through this analysis is close to values for the CEF splitting reported in the literature21. Thus, the major spin-decoherence mechanism at play is likely to be thermal excitation of crystal-field levels outside the Seff = 1/2 doublet, which presents defects in the chain that are able to change the number of spinons in the system on measurable timescales.
The coherence length encoded in the spinon lifetime exceeds ≈ 35 lattice units (ξ > 12 nm) and is comparable to the mesoscopic quantum coherence length of Haldane-gap magnons observed near zero temperature in spin-1 chains25. There, however, magnon coherence is quickly lost with the increasing temperature due to collisions that change the quasiparticle content of the excited states and therefore limit the quasiparticle lifetime25,27,28. Consequently, magnons become over-damped at temperatures where thermal energy becomes comparable to the energy of spin interactions. Remarkably, this collisional lifetime mechanism is absent in the case of spinons in the spin-1/2 chain as spinons retain their intrinsic coherence at temperatures much higher than those characteristic of the spin Hamiltonian.
Quantum Fisher information in the high-temperature limit
It is of interest to put our results in the context of quantum metrology, which allows calculating model-independent quantities called entanglement witnesses that can be used to place bounds on the degrees of multipartite quantum entanglement present in the system50,51. Of specific relevance is the quantum Fisher information (QFI), \({F}_{Q}(\hat{A})\)52, a quantity that can be defined at finite temperature for any system through an imaginary part of dynamical susceptibility with respect to a variable, \(\hat{A}\), in that system, \({\chi }_{A}^{{\prime\prime} }(E)\),
$${F}_{Q}(\hat{A})=\frac{1}{4\pi }\int_{0}^{\infty }dE\tanh \left(\frac{E}{2{k}_{B}T}\right){\chi }_{A}^{{\prime\prime} }(E)$$
(2)
For the spin-1/2 chain, the QFI, FQ, can be obtained for \(\hat{A}={\hat{S}}^{z}\) from the dynamical spin susceptibility at any wave-vector, χ″(Q, E). Equivalently, it can obtained from the dynamical spin structure factor, S(Q, E), measured by INS (Fig. 1), which is related to χ″(Q, E) via the fluctuation-dissipation theorem26,50,51. The obtained QFI can then be used to place lower limits on the level of multipartite entanglement in the system, where QFI FQ > n at a certain wave vector imply at least (n + 1)-partite entanglement in the system (Kramers-Rao bound)50,52,52 provided no symmetries are taken into account.
Figure 3C shows the wave-vector-dependent QFI calculated from our neutron spectra for temperatures down to 80 mK (open circles), as well as from our idealized DMRG model (solid curves). The dashed curve represents an approximation to the theoretical maximum at zero temperature, FQ∣T=0 = 4S(Q)49, where \(S(Q)=\int_{-\infty }^{\infty }S(Q,E)dE\) is static structure factor given by Fourier transform of the single-time two-point spin correlation function, obtained from DMRG calculations at 200 mK (≈ 0.01J/kB). The temperature dependence of the maximum quantum Fisher information FQ(L = 1) is shown in Fig. 3D with power-law fits to the asymptotic behavior for both experiment and the idealized DMRG model. Our analysis shows excellent agreement between DMRG and neutron scattering measurements at all temperatures above the magnetic ordering transition, TN ≈ 0.8 K. At very low temperatures, FQ in the idealized model continues to rise, demonstrating at least quadpartite entanglement at 200 mK. In contrast, in YbAlO3 the QFI is arrested with FQ ≈ 1 at TN, though enough spectral weight remains at high energy for it to demonstrate at least bipartite entanglement.
At high-temperature, FQ(L = 1) exhibits a near-perfect T−2 power-law decay for both experiment and theory. Already for temperatures T ≳ 0.5J/kB, FQ(L = 1) is below 1, the value where it indicates the presence of at least bipartite entanglement. Thus FQ as a metric for quantum coherence has limited usefulness at high temperatures. This poses a challenge of developing novel quantum metrology to capture high-temperature quantum behaviors in integrable systems, including the observed coherence of spinon excitations.
Real-space–time response
The observed long-range dynamical coherence associated with propagating spinons contrasts sharply with the local character of single-time two-spin correlation function, \(\langle {S}_{j}^{z}{S}_{{j}^{{\prime} }}^{z}\rangle \approx 1/4{\delta }_{j{j}^{{\prime} }}\) (\({\delta }_{j{j}^{{\prime} }}\) is Kronecker delta) at T ≫ J/kB, and classical expectation of non-propagative, over-damped or diffusive dynamics in this regime53. Like QFI, the single-time correlation is insensitive to dynamical coherence because it encodes an energy-integrated (single-time) property, static structure factor, S(Q). At high temperature, S(Q) ≈ 1/4 is Q-independent, indicating vanishing single-time spin-spin correlations.
The time-dependent, dynamical correlations revealing spinon coherence can be visualized by Fourier transforming the measured χ″(Q, E) to describe the real-space linear response, χ″(x, t)48 (See Supplementary Information for details of data and theoretical analysis and DMRG calculations.). This is shown in Fig. 4 as a sequence of color-plots scaled by the thermal factor T/J, where panels (A–D) show Fourier-transformed (FT) inelastic neutron data, (E–H) show the corresponding Fourier-transforms of our fits to the data, and (I–L) show the space-time theoretical DMRG data. At all temperatures, χ″(x, t) is measurably nonzero only in a region defined by a coherent “light cone” bounded by the spinon velocity and approaching zero width at the origin (x → 0 as t → 0) in line with purely local single-time correlations. This light cone feature corresponds in the wave-vector-energy domain to the dispersive upper boundary of the spinon spectrum, and its presence at high temperatures testifies to the coherent nature of excitations. Remarkably, the linear ballistic transport regime appears to persist on a mesoscopic length scale at short times even when the thermal energy scale markedly exceeds interactions. At long times, however, the transport appears to cross over into a super-diffusive regime, x ~ t 2/3. Such a super-diffusive behavior is predicted in the high-temperature limit of the Heisenberg chain and has been of interest for some number of years54, but to our knowledge this is the clearest experimental signature of such a behavior to date. At very high temperatures, experiment and fits experience a Lorentzian broadening along the energy axis, which indicates a shortening of the coherence time and a faster decay of dynamical correlations absent in the purely theoretical model, Fig. 4(I–L).