Model system
We use the Generalized Holstein-Tavis-Cummings (GHTC) Hamiltonian23,24,25,26 to describe N excitons interacting with \({{{\mathcal{M}}}}\) cavity modes, and \(N\gg {{{\mathcal{M}}}}\) in line with typical experimental conditions. Typically, one estimates \(N/{{{\mathcal{M}}}} \sim 1{0}^{6}-1{0}^{9}\) for systems used in experiments27. The total Hamiltonian can be written in the form of the system-bath model and is expressed as \(\hat{H}={\hat{H}}_{{{{\rm{S}}}}}+{\hat{h}}_{{{{\rm{B}}}}}+{\hat{H}}_{{{{\rm{SB}}}}}\). The system Hamiltonian \({\hat{H}}_{{{{\rm{S}}}}}\) consists of the excitonic degrees of freedom (DOF) and the photonic DOF of the cavity. Each exciton is modeled as an effective two-level system that consists of the ground state \(\left\vert {g}_{n}\right\rangle\) and excited state \(\left\vert {e}_{n}\right\rangle\) (for the nth exciton). Without making the long-wavelength approximation26, \({\hat{H}}_{{{{\rm{S}}}}}\) is expressed as follows,
$${\hat{H}}_{{{{\rm{S}}}}}= \hslash {\omega }_{0}{\sum}_{n=1}^{N}{\hat{\sigma }}_{n}^{{{\dagger}} }{\hat{\sigma }}_{n}+{\sum}_{k}^{{{{\mathcal{M}}}}}\hslash {\omega }_{k}{\hat{a}}_{k}^{{{\dagger}} }{\hat{a}}_{k}\\ + {\sum}_{k}{\sum}_{n=1}^{N}\hslash {g}_{k}\left[{\hat{a}}_{k}^{{{\dagger}} }{\hat{\sigma }}_{n}{e}^{-i{k}_{\parallel }\cdot {x}_{n}}+{\hat{\sigma }}_{n}^{{{\dagger}} }{\hat{a}}_{k}{e}^{i{k}_{\parallel }\cdot {x}_{n}}\right] \hfill,$$
(1)
where \({\hat{\sigma }}_{n}^{{{\dagger}} }=\left\vert {e}_{n}\right\rangle \left\langle {g}_{n}\right\vert\) and \({\hat{\sigma }}_{n}=\left\vert {g}_{n}\right\rangle \left\langle {e}_{n}\right\vert\) are the creation and annihilation operators of the nth molecule’s exciton, and ω0 is the excitation energy between the molecule’s ground and excited state. Furthermore, \({\hat{a}}_{k}\) and \({\hat{a}}_{k}^{{{\dagger}} }\) are the photonic field annihilation and creation operators for mode k whose frequency is ωk. Note that the GHTC model described here does not contain exciton inter-site hopping or exciton-exciton interactions, which might prove to be important for a realistic description of polariton transport.
For Fabry–Pérot (FP) cavities, the dispersion is
$${\omega }_{k}({k}_{\parallel })=c\sqrt{{k}_{\perp }^{2}+{k}_{\parallel }^{2}},$$
(2)
where c is the speed of light in vacuum. When k∥ = 0, the photon frequency is ωc ≡ ωk(k∥ = 0) = ck⊥. The second line of Eq. (1) represents light-matter interaction, where \({g}_{k}={g}_{{{{\rm{c}}}}}\sqrt{({\omega }_{k}/{\omega }_{{{{\rm{c}}}}})}\cos \theta\) is the k-dependent light-matter coupling strength4, and \(\tan \theta={k}_{\parallel }/{k}_{\perp }\) is the incident angle. Note that the θ angle inside the cavity differs from the angle of incidence outside the cavity if the cavity background refractive index is not 1. Furthermore, xn is the position of the nth exciton. We consider the cavity modes inside the same simulation box as the excitons, with total size NL along the k∥ direction (L = xn − xn−1).
As such, k∥ has discrete (but quasi-continuous) values of \({k}_{\parallel }=\frac{2\pi }{NL}k\), where the mode index is \(k\in [-\frac{{{{\mathcal{M}}}}-1}{2},…0,…\frac{{{{\mathcal{M}}}}-1}{2}]\). Diagonalizing \({\hat{H}}_{{{{\rm{S}}}}}\) in the singly excited subspace leads to \(2{{{\mathcal{M}}}}\) polariton states \(\left\vert {\pm }_{k}\right\rangle\), with eigen-energies
$${\epsilon }_{\pm k}=\hslash {\omega }_{\pm k}=\frac{\hslash }{2}({\omega }_{k}+{\omega }_{0})\pm \frac{\hslash }{2}\sqrt{{({\omega }_{k}-{\omega }_{0})}^{2}+4N{g}_{k}^{2}},$$
(3)
where + and − denote the upper polariton (UP) and LP branches, respectively. In addition, there are \(N-{{{\mathcal{M}}}}\) dark states \(\left\vert {{{{\mathcal{D}}}}}_{k}\right\rangle\) with energies \(\hslash {\omega }_{{{{\mathcal{D}}}}k}=\hslash {\omega }_{0}\), which do not mix with photonic states and form the dark exciton branch. The definition of these dark states is provided in Supplementary Note 1.
Under the polariton representation, the system Hamiltonian in Eq. (1) is expressed as \({\hat{H}}_{{{{\rm{S}}}}}={\sum }_{\mu,k}\hslash {\omega }_{\mu k}{\hat{P}}_{\mu,k}^{{{\dagger}} }{\hat{P}}_{\mu,k}\), where \({\hat{P}}_{\mu,k}^{{{\dagger}} }\), \({\hat{P}}_{\mu,k}\) are the polariton creation and annihilation operators for polariton state k on polariton band μ, respectively, and the band label \(\mu \in \{+, – , {{{\mathcal{D}}}}\}\). Specifically,
$${\hat{P}}_{+,k}^{{{\dagger}} }= \cos {\Theta }_{k}{\hat{B}}_{k}^{{{\dagger}} }+\sin {\Theta }_{k}{\hat{a}}_{k}^{{{\dagger}} }$$
(4a)
$${\hat{P}}_{-,k}^{{{\dagger}} }=-\sin {\Theta }_{k}{\hat{B}}_{k}^{{{\dagger}} }+\cos {\Theta }_{k}{\hat{a}}_{k}^{{{\dagger}} },$$
(4b)
where \({\hat{B}}_{k}^{{{\dagger}} }=(1/\sqrt{N}){\sum }_{n=1}^{N}{e}^{-i{k}_{\parallel }\cdot {x}_{n}}{\hat{\sigma }}_{n}^{{{\dagger}} }\) creates the collective bright excitons, and
$${\Theta }_{k}=\frac{1}{2}\arctan \left(\frac{2\sqrt{N}{g}_{k}}{{\omega }_{k}-{\omega }_{0}}\right)\in \left[0,\frac{\pi }{2}\right)$$
(5)
is the mixing angle. Details on the derivation in the polariton representation, as well as the expressions of the polariton operators, are provided in Supplementary Note 1. We present a schematic illustration of the model system above, as well as the polariton band structure, in Fig. 1. Without coupling to phonons, the polariton exhibits band-like transport characterized by the group velocity
$${v}_{g,\pm }({k}_{\parallel })=d{\omega }_{\pm k}/d{k}_{\parallel },$$
(6)
where the k∥-dependence of ω±k is carried by ωk via Eq. (2).
Fig. 1: Schematics of the GHTC model and band structure.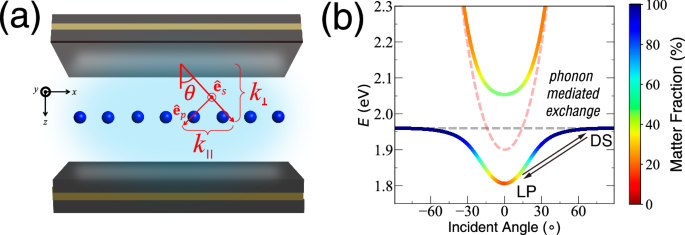
a Schematics of the model setup. Inside an optical cavity, the separated molecules collectively interact with many cavity modes. b Polariton band structure, where the matter fraction is shown in terms of the colorbar. The dashed lines are the bare photon (red) and matter (silver) dispersions, respectively. The phonon-mediated exchange effect between the lower polariton (LP) and the dark states (DS) manifold is also indicated, which is the main cause of polariton group velocity renormalization.
The bath Hamiltonian \({\hat{h}}_{{{{\rm{B}}}}}\) describes the nuclear DOF, which we assume is a phonon environment that consists of a set of non-interacting harmonic oscillators, \({\hat{h}}_{{{{\rm{B}}}}}={\sum }_{n=1}^{N}{\sum }_{\alpha }\hslash {\omega }_{\alpha }{\hat{b}}_{\alpha,n}^{{{\dagger}} }{\hat{b}}_{\alpha,n}\), where \({\hat{b}}_{\alpha,n}\), \({\hat{b}}_{\alpha,n}^{{{\dagger}} }\) are the αth bosonic bath phonon annihilation and creation operators in the nth molecule with phonon frequency ωα. Furthermore, \({\hat{H}}_{{{{\rm{SB}}}}}\) describes the exciton-phonon interaction \({\hat{H}}_{{{{\rm{SB}}}}}=\mathop{\sum }_{n=1}^{N}{\hat{\sigma }}_{n}^{{{\dagger}} }{\hat{\sigma }}_{n}\otimes {\sum }_{\alpha }{c}_{\alpha }({\hat{b}}_{\alpha,n}+{\hat{b}}_{\alpha,n}^{{{\dagger}} })\), where cα is the exciton-phonon coupling strength. We assume the coupling strength is identical for all excitons and cα is therefore independent of the label n. Based on the Caldeira–Leggett model28,29, the baths as well as their interactions with the system are described by the spectral density
$$J(\omega )=\frac{\pi }{\hslash }\mathop{\sum}_{\alpha }{c}_{\alpha }^{2}\delta (\omega -{\omega }_{\alpha }),$$
(7)
and \(\lambda=(1/\pi )\int_{0}^{+\infty }d\omega \; \,J(\omega )/\omega={\sum }_{\alpha }{c}_{\alpha }^{2}/{\omega }_{\alpha }\) is the reorganization energy.
We further introduce the Fourier transform of the bath phonon operators \({\hat{b}}_{\alpha,k}=(1/\sqrt{N}){\sum }_{n=1}^{N}{e}^{\,i{k}_{\parallel }\cdot {x}_{n}}{\hat{b}}_{\alpha,n}\). Using these transforms, the bath Hamiltonian is expressed as \({\hat{h}}_{{{{\rm{B}}}}}={\sum }_{k}{\sum }_{\alpha }\hslash {\omega }_{\alpha }{\hat{b}}_{\alpha,k}^{{{\dagger}} }{\hat{b}}_{\alpha,k}\), and the polariton-phonon interaction Hamiltonian is given by
$${\hat{H}}_{{{{\rm{SB}}}}}={\sum}_{\mu,k,\nu,{k}^{{\prime} }}{\zeta }_{\mu k}\cdot {\zeta }_{\nu {k}^{{\prime} }}{\hat{P}}_{\mu,k}^{{{\dagger}} }{\hat{P}}_{\nu,{k}^{{\prime} }}{\sum}_{\alpha }\frac{{c}_{\alpha }}{\sqrt{N}}\left({\hat{b}}_{\alpha,k-{k}^{{\prime} }}+{\hat{b}}_{\alpha,{k}^{{\prime} }-k}^{{{\dagger}} }\right),$$
(8)
where the band labels \(\mu,\nu \in \{+,-,{{{\mathcal{D}}}}\}\), and ζμk is a state-dependent coefficient that characterizes the matter fraction of the polariton state, with \({\zeta }_{+k}=\cos {\Theta }_{k}\) and \({\zeta }_{-k}=\sin {\Theta }_{k}\). The ζ+k and ζ−k are commonly referred to as the Hopfield coefficients24,30,31, and we note that \({\zeta }_{{{{\mathcal{D}}}}k}=1\). These polariton-phonon interactions will modify the polariton band structure, and will, in turn, affect the polariton transport properties such as the group velocity in Eq. (6).
Theory
We derive the expression for vg-renormalization using the equilibrium Green’s functions at finite temperature. We restrict our discussions to polariton transport in the weak exciton-phonon coupling regime and the band-like transport regime4,6. The single-particle Green’s function of the polaritons at finite temperature is expressed as follows32,
$${G}_{\mu,k}(t)\equiv -i\theta (t)\langle {\hat{P}}_{\mu,k}(t){\hat{P}}_{\mu,k}^{{{\dagger}} }(0)\rangle,$$
(9)
where θ(t) is the Heaviside step function, the time-dependence of the operators read as \({\hat{P}}_{\mu,k}(t)={e}^{\frac{i}{\hslash }\hat{H}t}{\hat{P}}_{\mu,k}(0){e}^{-\frac{i}{\hslash }\hat{H}t}\), and \(\langle \hat{A}\rangle \equiv \,{{\mbox{Tr}}}\,[\hat{A}{e}^{-\beta \hat{H}}]/\,{{\mbox{Tr}}}\,[{e}^{-\beta \hat{H}}]\) denotes the thermal average under finite temperature β ≡ 1/(kBT), where kB is the Boltzmann constant. Similarly, one defines the Green’s function of the phonons as \({D}_{q}(t)\equiv -i{\sum }_{\alpha }({c}_{\alpha }^{2}/N)\cdot \langle {{{\mathcal{T}}}}({\hat{b}}_{\alpha,q}(t)+{\hat{b}}_{\alpha,-q}^{{{\dagger}} }(t))({\hat{b}}_{\alpha,-q}(0)+{\hat{b}}_{\alpha,q}^{{{\dagger}} }(0))\rangle\), where \({{{\mathcal{T}}}}\) is the time-ordering operator. The Green’s function in Eq. (9) can be determined by the self-consistent Dyson equation in the time domain as32
$$\left(i\hslash \frac{\partial }{\partial t}-{\epsilon }_{\mu k}\right){G}_{\mu,k}(t)-\int_{0}^{t}d\tau \,{\Sigma }_{\mu,k}(t-\tau ){G}_{\mu,k}(\tau )=\delta (t),$$
(10)
where Σμ,k(t) is the self-energy, and ϵμk = ℏωμk is the bare polariton energy. Eq. (10) is recast in the frequency domain as
$${{{{\mathcal{G}}}}}_{\mu,k}^{-1}(\omega )=\hslash (\omega -{\omega }_{\mu k}+i\eta )-{\Sigma }_{\mu,k}(\omega ),$$
(11)
where \({{{{\mathcal{G}}}}}_{\mu,k}(\omega )\) is the Fourier transform of Gμ,k(t), and we take η → 0+. To obtain the polariton band renormalization, we further define the renormalized polariton energies \({\tilde{E}}_{\mu k}={E}_{\mu k}+i{\Gamma }_{\mu k}\) and plug it into Eq. (11), arriving at the expression33
$${E}_{\mu k}=\hslash {\omega }_{\mu k}+\,{{\mbox{Re}}}\,[{\Sigma }_{\mu,k}({\tilde{E}}_{\mu k}/\hslash )],$$
(12)
$${\Gamma }_{\mu k}=\,{{\mbox{Im}}}\,[{\Sigma }_{\mu k}({\tilde{E}}_{\mu k}/\hslash )],$$
(13)
which has to be solved self-consistently for Eμk and Γμk. Consequently, Eμk is the renormalized polariton band, and the renormalized polariton group velocity is obtained via \({\tilde{v}}_{g,\pm }({k}_{\parallel })=(1/\hslash )d{E}_{\pm k}/d{k}_{\parallel }\), which leads to
$${\tilde{v}}_{g,\pm }({k}_{\parallel })={v}_{g,\pm }({k}_{\parallel })+\frac{1}{\hslash }\frac{d}{d{k}_{\parallel }}\,{{\mbox{Re}}}\,\left[{\Sigma }_{\pm,k}({\tilde{E}}_{\pm k}/\hslash )\right].$$
(14)
The second term in the right-hand side of Eq. (14) characterizes the modification of the polariton group velocity due to polariton-phonon interaction. We hypothesize that this term is the main cause of the renormalization of vg4,21.
In most cases, Eq. (12) cannot be solved exactly, and approximations are needed to obtain the self-energy in a closed form. Here, we derive the leading contribution to polariton band renormalization using the standard tools of diagrammatic perturbation theory. The first-order self-energy is expressed as32,34,35
$${\Sigma }_{\mu,k}^{(1)}(t)=i{\zeta }_{\mu k}^{2}{\sum}_{{{{\boldsymbol{\nu}}}},{k}^{{\prime} }}{\zeta }_{{{{\boldsymbol{\nu}}}} {k}^{{\prime} }}^{2}\cdot {D}_{k-{k}^{{\prime} }}^{(0)}(t){G}_{{{{\boldsymbol{\nu}}}},{k}^{{\prime} }}^{(0)}(t),$$
(15)
where \({G}_{\pm,k}^{(0)}(t)=-i\theta (t){e}^{-i{\omega }_{\pm k}t}\) and \({G}_{{{{\mathcal{D}}}},k}^{(0)}(t)=-i\theta (t){e}^{-i{\omega }_{0}t}\) are the non-interacting Green functions of the polaritons and the dark excitons, respectively, and the low-temperature limit is taken because ϵμk ≫ kBT. Furthermore, \({D}_{k-{k}^{{\prime} }}^{(0)}(t)\) is the free phonon propagator under finite temperature, and is expressed as
$${D}_{q}^{(0)}(t)=-i{\sum}_{\alpha }\frac{2{c}_{\alpha }^{2}}{N}[(1+{\overline{n}}_{\alpha }){e}^{-i{\omega }_{\alpha }| t| }+{\overline{n}}_{\alpha }{e}^{\,i{\omega }_{\alpha }| t| }],$$
(16)
where \({D}_{q}^{(0)}(t)\) is independent of q, \({\overline{n}}_{\alpha }=1/({e}^{\beta \hslash {\omega }_{\alpha }}-1)\) is the Bose-Einstein distribution function, and the bath modes are degenerate such that ωα,q = ωα,−q = ωα. A diagrammatic representation for the polariton Green’s functions and self-energies are provided in Supplementary Fig. 1. Eq. (15) is the Fan-Migdal self-energy33, and when substituted in Eq. (14), leads to the following expression for the modified polariton bands
$${E}_{\mu k}^{(2)}=\hslash {\omega }_{\mu k}+{\zeta }_{\mu k}^{2}\cdot {\sum}_{\nu,{k}^{{\prime} }}{\sum}_{\alpha }{\zeta }_{\nu {k}^{{\prime} }}^{2}\cdot \frac{2{c}_{\alpha }^{2}}{N}\cdot {\Xi }_{\mu k,\nu {k}^{{\prime} }}({\omega }_{\alpha }),$$
(17)
where \({\Xi }_{\mu k,\nu {k}^{{\prime} }}({\omega }_{\alpha })\) is the real part of the polarizability and is given by
$${\Xi }_{\mu k,\nu {k}^{{\prime} }}({\omega }_{\alpha })=\,{{\mbox{Re}}}\,\left[\frac{1+{\overline{n}}_{\alpha }}{{\omega }_{\mu k}-{\omega }_{\nu {k}^{{\prime} }}-{\omega }_{\alpha }+i\eta }+\frac{{\overline{n}}_{\alpha }}{{\omega }_{\mu k}-{\omega }_{\nu {k}^{{\prime} }}+{\omega }_{\alpha }+i\eta }\right].$$
(18)
A detailed derivation of Eq. (18) is provided in Supplementary Note 2. For continuous spectral density functions, the summation over the phonon modes α in Eq. (17) can be written as an integral in terms of J(ω) (see Supplementary Note 3). We note that the band modification can also be obtained directly from the total Hamiltonian using Rayleigh-Schrödinger perturbation theory33, by treating \({\hat{H}}_{{{{\rm{SB}}}}}\) as perturbative interactions that cause 2nd-order energy corrections (that scatter \(\left\vert -,k\right\rangle\) to dark states then scatter back). This derivation is provided in Supplementary Note 2D, with the results identical to Eq. (17) (with η = 0).
In this work, we focus on the LP’s vg renormalization, which is dominated by scattering to the dark exciton states (a total of \(N-{{{\mathcal{M}}}}\) of them), as opposed to scattering to the \({{{\mathcal{M}}}}\) LP and \({{{\mathcal{M}}}}\) UP states because \(N-{{{\mathcal{M}}}}\gg 2{{{\mathcal{M}}}}\). Thus, one can explicitly perform the summation over \({k}^{{\prime} }\) that only includes the dark exciton contributions with \({\sum }_{{k}^{{\prime} }}f({\omega }_{\nu {k}^{{\prime} }})\approx (N-{{{\mathcal{M}}}})f({\omega }_{0})\), and the \(N-{{{\mathcal{M}}}}\) factor will cancel with 1/N in Eq. (17) under the large N limit. The validity of this approximation is further demonstrated numerically in Supplementary Fig. 2. This cancellation also indicates that in simulations, as long as one can keep \((N-{{{\mathcal{M}}}})/N\to 1\), one should expect the same converged results, and the detailed choice of N or \({{{\mathcal{M}}}}\) does not matter that much (assuming sufficient resolution of the polariton wavepacket in the spatial and k-space).
With the above considerations, the renormalized LP group velocity becomes
$${\tilde{v}}_{g,-}={v}_{g,-}+\frac{d}{d{k}_{\parallel }}\left[| {C}_{k}{| }^{2}{\sum}_{\alpha }2{c}_{\alpha }^{2}\cdot {\Xi }_{-k,0}({\omega }_{\alpha })\right],$$
(19)
where the Hopfield coefficient ∣Ck∣2 is expressed as
$$| {C}_{k}{| }^{2}={\sin }^{2}{\Theta }_{k}=\frac{1}{2}\left[1+\frac{{\omega }_{k}-{\omega }_{0}}{\sqrt{{({\omega }_{k}-{\omega }_{0})}^{2}+4N{g}_{k}^{2}}}\right],$$
(20)
which characterizes the matter fraction of the LP. Furthermore, Ξ−k,0(ωα) only considers the dark exciton contribution and is expressed as
$${\Xi }_{-k,0}({\omega }_{\alpha })=\frac{{\overline{n}}_{\alpha }\cdot ({\omega }_{\alpha }-\Delta {\omega }_{-k})}{{({\omega }_{\alpha }-\Delta {\omega }_{-k})}^{2}+{\eta }^{2}}-\frac{1+{\overline{n}}_{\alpha }}{{\omega }_{\alpha }+\Delta {\omega }_{-k}},$$
(21)
where Δω−k = ω0 − ω−k > 0 is the energy gap between the dark exciton states and the LP band at \({k}_{\parallel }=\frac{2\pi }{NL}k\). Eq. (19) provides an analytic expression of the LP group velocity based on the current theory. It predicts that the magnitude of the vg renormalization will depend linearly on λ [through \({c}_{\alpha }^{2}\)], and also predicts that vg is sensitive to Ck and temperature [through \({\overline{n}}_{\alpha }\)]. In Supplementary Fig. 3, we present the plot of the amplitude of vg renormalization against the matter fraction ∣Ck∣2, and against the temperature, respectively. Further taking the η → 0 limit of Eq. (21), one can analytically express Eq. (19) as
$$\begin{array}{rcl}\Delta {v}_{g,-}&\equiv &{\tilde{v}}_{g,-}-{v}_{g,-}\hfill\\ &=&-\frac{d}{d{k}_{\parallel }}\left[| {C}_{k}{| }^{2}{\sum} _{\alpha }2{c}_{\alpha }^{2}{\omega }_{\alpha }\frac{\Delta {\omega }_{-k}\cdot (2{\overline{n}}_{\alpha }+1)-{\omega }_{\alpha }}{\Delta {\omega }_{-k}^{2}-{\omega }_{\alpha }^{2}}\right].\end{array}$$
(22)
In most experiments, the LP initial excitation is in a region Δω−k ≫ ωα, thus Ξ−k,0(ωα) is negative. For a broad range of phonon frequencies, the high-frequency phonon makes a positive contribution to Ξ−k,0(ωα), but the overall results should still be dominated by the low-frequency phonons, making Ξ−k,0(ωα) negative. Note that Eq. (19) is only valid when dark excitons dominate the sum in Eq. (17). Nevertheless, one is able to derive simpler analytic answers from Eq. (17) or Eq. (19) under different regimes of spectral densities J(ω) or temperatures.
Mechanistic picture
We want to comment on the mechanistic picture suggested by Eqs. (22) and (17). The LP group velocity renormalization occurs mainly due to the presence of the dark states as a virtual scattering state. The transition from LP to all dark states, and scattering back to the LP (\(\left\vert -,k\right\rangle \to \left\vert {{{\mathcal{D}}}}\right\rangle \to \left\vert -,k\right\rangle\)) leads to the reduction of the group velocity, which can be understood as the perturbative energy correction up to second order. Indeed, the overall scaling of Δvg,− ∝ 1/Δω−k. This scaling means that even with large light matter detunings, such that the dark states are never appreciably populated from the LP, these dark states still act like virtual states, such that their perturbative presence will lead to energy correction of LP and hence vg renormalization. In this sense, we can classify the physical picture predicted by Eq. (22) as the super-exchange-like mechanism, where the dark exciton states act like virtual states to mediate the population transfer with LP. For small light-matter detuning (such as in ref. 3), the LP might be able to transfer the population to the dark states. Note that the typical super-exchange process describes indirect energy transfer to another state mediated by virtual states, rather than back to the initial state36,37. For a large light-matter detuning, dark states will only be virtually populated and thus will not be detected spectroscopically, as experimentally observed under resonant excitation of the LP in ref. 4. Supplementary Fig. 5 presents the polariton band structure and group velocity modification under different detunings, and Supplementary Fig. 6 presents a two-dimensional “heat map” of the detuning effect under different ωc and k∥. Furthermore, Supplementary Fig. 7 presents the population dynamics of the polariton and dark states obtained from Ehrenfest dynamics simulations under different detunings. We also note that the mechanism is akin to the Raman scattering process, which is evidenced by the expression of \({\Xi }_{\mu k,\nu {k}^{{\prime} }}({\omega }_{\alpha })\) in Eq. (18). In fact, Eq. (17) is the Raman-type polarizability in the frequency domain, which is the well-known Kramers–Heisenberg–Dirac (KHD) expression38,39,40,41, but now with temperature dependence (because the interaction is \({\hat{H}}_{{{{\rm{SB}}}}}\), which is temperature dependent, and not the dipole interaction with the field in the original KHD expression). Supplementary Note 2D clearly shows how the \({\hat{H}}_{{{{\rm{SB}}}}}\) term mediates the transition from LP to dark states and back to LP bands. As such, the vg-renormalization can also be described as a phonon-mediated Raman-type scattering process, which is a non-resonant process. A schematic illustration is provided in Fig. 1b. Finally, the mechanism is also akin to the model used in the quantum relaxation process (see Chapter 9 of ref. 29).
Note that under the polariton representation, an alternative mechanistic picture could be phonon-mediated attractive interactions between polaritons and dark excitons, manifested by the negative energy correction in Eq. (17) (and one can further obtain an effective interacting polariton Hamiltonian via a Schrieffer–Wolff transformation32,42,43, for example). In this sense, polariton attractions provide a backward drag force to the polariton wavefront and slow down the propagation. This mechanistic picture is consistent with the dark states manifold-mediated scattering effect discussed above. Note that the above-mentioned is just an interpretation, and the current theory or simulations do not explicitly consider the many-body interactions (such as exciton-exciton or polariton-polariton interactions).
We emphasize that the current theory predicts a less sensitive bath characteristic phonon frequency ωf dependence of vg. See Supplementary Fig. 8 for details. Nevertheless, increasing ωf could lead to a more significant LP → DS population transfer, which breaks the equilibrium theory (See Supplementary Fig. 9). On the other hand, when increasing the light-matter detunings so that LP → DS population transfer is suppressed, Supplementary Fig. 10 shows that vg is indeed less sensitive to ωf. Furthermore, we emphasize that the polariton band modification expressed in Eq. (17), or approximately [c.f. Eq. (19)], \({E}_{-,k}^{(2)}\approx \left[| {C}_{k}{| }^{2}{\sum }_{\alpha }2{c}_{\alpha }^{2}\cdot {\Xi }_{-k,0}({\omega }_{\alpha })\right]\) does not cause the shift of the optical signal44. For angle-resolved cavity photonic spectra, our results indicate that in optical measurements of the polariton dispersion, phonon coupling will only broaden the spectra, not change the peak frequency or band dispersion (see Supplementary Fig. 11). As such, \({E}_{-,k}^{(2)}\) is a unique quantity that renormalizes the group velocity, but does not directly influence linear optical signals. Our model thus closely matches experimental measurements that display no measurable renormalization of the polariton dispersion measured from linear reflectance or transmission spectra, but a large group velocity renormalization in nonequilibrium measurements of polariton propagation.
Numerical results
To quantitatively examine the accuracy of the above theory (Eq. (17), or the corresponding \({\tilde{v}}_{g,-}\)), we perform quantum dynamics simulations for the GHTC model Hamiltonian using the Ehrenfest method21, and verify various scaling relations and predictions made by the theory. For the system Hamiltonian, we chose the exciton energy ℏω0 = 1.96 eV, the cavity frequency ℏωc = 1.90 eV, and the collective light-matter coupling strength \(\sqrt{N}{g}_{{{{\rm{c}}}}}=120\) meV. Details of the models and computations are provided in Supplementary Note 4, with a brief summary provided in the “Methods” section.
Figure 2 a presents the modified polariton band structure (Eq. (17)) with different λ. One observes that the modification of vg increases as λ and the matter fraction increase. For the LP branch, the second term in Eq. (17) is negative, which effectively provides an attractive interaction between polaritons (mediated by phonons) and decreases the LP energy. Since \({\zeta }_{\mu k}^{2}\) is the matter fraction of the polariton branch, it is straightforward to see that as k∥ increases, \({\zeta }_{-k}^{2}\) increases with a larger matter fraction, thus providing more modifications to the LP band. The modified polariton band structure consequently leads to polariton group velocity renormalization. Note that when both λ and k∥ are large, the polariton dispersions bend down and have a negative slope (red and green curves in Fig. 2a), implying that \({\tilde{v}}_{g,-}\) becomes negative. This behavior is unphysical due to the breakdown of the perturbation theory used to derive Eq. (17). The quantum dynamics simulations21 suggest that under this regime, the transport will become diffusive with a very small vg. For the results presented later, we only focus on the region of k∥ ≥ 0 predicted by the analytic theory in Eq. (19).
Fig. 2: Polariton energy and group velocity renormalization due to polariton-phonon interaction.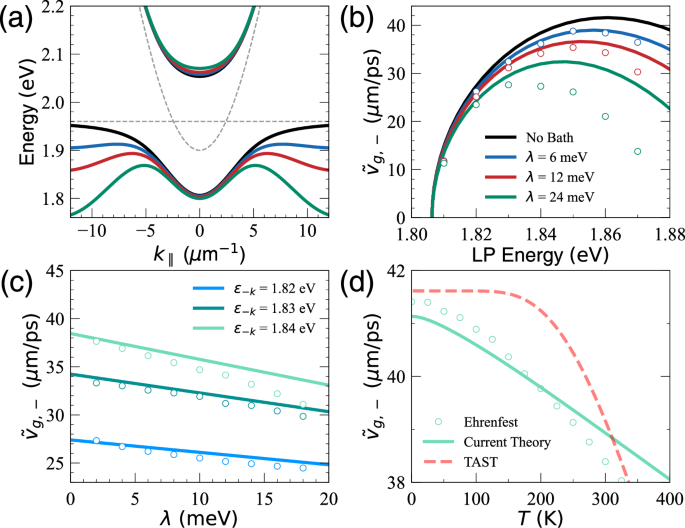
a Modified polariton band structure under different λ. b Group velocity of the LP branch \({\tilde{v}}_{g,-}\) as a function of the bare LP energy (black curve in (a)). under different λ. c Scaling relation of the LP group velocity \({\tilde{v}}_{g,-}\) with λ. d Temperature-dependence of the LP group velocity \({\tilde{v}}_{g,-}\) at LP energy ϵ−k = 1.86 eV and λ = 6 meV. Theoretical results using Eq. (17) (solid lines) are compared to Ehrenfest dynamics simulations (open circles).
Figure 2b presents the LP group velocity as a function of the bare LP energies (see the black curve in Fig. 2a) and for different λ, where the theoretical results using Eq. (17) are compared to quantum dynamics simulations (open circles). One sees that as λ increases, the magnitude of the group velocity renormalization increases (from the blue curve to the green curve), further deviating from the derivative of the LP band, vg (black solid curve). Furthermore, as the LP energy increases, the matter character of the LP state \(| {C}_{k}^{2}|\) also increases, which further reduces the group velocity. For all cases, the theory agrees very well with the numerical simulations for small λ (λ, the polariton-phonon interaction enters the non-perturbative regime, and the first-order self-energy level theory in Eq. (17) becomes inadequate. As a result, the theory gradually deviates from numerical simulations, as expected. Nevertheless, the theory describes the overall semi-quantitative trend of the data from the simulation.
Figure 2c presents the scaling relation of the LP group velocity \({\tilde{v}}_{g,-}\) (c.f. Eq. (19)) as a function of λ, which characterizes the modification to the LP group velocity by the polariton-phonon interaction. Importantly, the theory in Eq. (19) predicts that this renormalization magnitude is proportional to \({c}_{\alpha }^{2}\) and thus \(| \Delta {v}_{g,-}|=| {\tilde{v}}_{g,-}-{v}_{g,-}| \propto \lambda\). Figure 2c presents \({\tilde{v}}_{g,-}\) versus λ at different LP energies. We observe that \({\tilde{v}}_{g,-}\) scales linearly with λ, and the slope increases as the matter fraction increases. It is clear from Eq. (17) that the polariton band structure (or group velocity) modification is proportional to λ due to its quadratic dependence on cα. The results obtained from quantum dynamics simulations agree quite well with the theory, especially for cases with small λ and matter fractions. As λ and matter fraction increase, the Ehrenfest results gradually deviate from the theory and show a nonlinear dependence on λ, due to non-perturbative effects; see the ϵ−k = 1.84 eV (shallow green) curve for example. Nevertheless, the semi-quantitative trend is always captured by the theory, and we stress that there are no free parameters in the current theory. Furthermore, our quantum dynamics simulation is based on the Ehrenfest MQC approximation, which may lead to inaccurate results when λ is large. Future efforts are needed to evaluate vg in the large λ regime using more accurate quantum dynamics approaches.
Figure 2d presents the temperature dependence of the polariton group velocity renormalization. Figure 2d presents \({\tilde{v}}_{g,-}\) versus T at LP energy ϵ−k = 1.86 eV and λ = 6 meV. From a theoretical standpoint, the temperature dependence is mainly carried by the Bose–Einstein distribution function in Eq. (17), which is nonlinear in T. In particular, under the high-temperature limit (ℏωα ≪ kBT for all ωα), the Bose-Einstein distribution function can be approximated as \({\overline{n}}_{\alpha }\approx {k}_{{{{\rm{B}}}}}T/(\hslash {\omega }_{\alpha })\propto T\). As a result, the modification of the polariton band structure (or group velocity) is proportional to T. At temperatures near 300 K, the parameters we used satisfy the high-temperature limit; thus Δvg,− scales linearly with T. In the Ehrenfest dynamics simulations, the nuclear quantum effect comes from the initial Wigner distribution of the nuclear thermal density only, and the exciton-phonon dynamics beyond the quantum-classical limit are not captured. Considering this, the deviation between Ehrenfest dynamics and the theory is likely due to the inaccuracy of Ehrenfest dynamics at very low temperatures, as we expect that our analytic theory should be accurate under the low λ, even when T → 0 limits (because there is no additional approximations related to the temperature dependence factor in Eq. (21)). Nevertheless, both the current theory (solid green line) and the numerical simulation agree reasonably well across all temperature regimes. Overall, the theory and simulations predict that vg,− decreases as T increases. This is because when T increases, the phonon fluctuations cause transitions from the LP band to the dark exciton states, thus reducing the group velocity. We also want to emphasize that there is no free parameter in the current theory to predict the temperature dependence.
Note that a phenomenological expression has previously been proposed based on the TAST6, due to scattering from \(\left\vert {-}_{k}\right\rangle\) to the dark states, resulting in the following expression for the group velocity renormalization
$${\tilde{v}}_{g,-}=\frac{{v}_{g,-}}{1+G\cdot {e}^{-\beta \hslash \Delta {\omega }_{-k}}},$$
(23)
where G is a free parameter. See Supplementary Note 5, as well as Supplementary Information S3 in ref. 6 for further details. The TAST is based on the idea that transport depends on the proportion of time the system spends in the LP band relative to the dark states, resulting in a temperature-dependent modification of vg that is sensitive to the energy gap Δω−k. Although the TAST makes intuitive sense (and aligns with findings from our microscopic theory), we found that Eq. (23) does not give the correct temperature dependence when G is treated as a temperature-independent parameter. In Fig. 2, the result from TAST is plotted as the red dashed curve, with a fitting parameter G = 3.0 to reproduce the correct value of \({\tilde{v}}_{g,-}\) at T = 300 K. One sees that it does not give the correct T-dependence across a broad range of temperatures unless one further chooses a T-dependent G parameter. The reason TAST fails to reproduce an accurate T-dependence is because the expression from TAST scales as \(1/(1+{e}^{-\beta \hslash \Delta {\omega }_{-k}})\), whereas the microscopic theory in Eq. (19) posits that the temperature dependence is \({\overline{n}}_{\alpha }\approx {e}^{-\beta \hslash {\omega }_{\alpha }}\) under the low-temperature limit when ℏωα ≫ kBT, and \({\overline{n}}_{\alpha }\approx {k}_{{{{\rm{B}}}}}T/(\hslash {\omega }_{\alpha })\) under the high-temperature limit when ℏωα ≪ kBT. Additionally, TAST assumes that the transition between the LP band and dark exciton states follows Boltzmann statistics, whereas, in our current theory, the phonons obey Bose-Einstein statistics, which mediate the (virtual) transitions between the LP band and the dark states. Our microscopic theory also predicts that Δvg,− should depend on Δω−k, but this dependence (in Eq. (19)) is not in the Boltzmann factor. As such, at a low temperature when kBT ≪ ℏΔω−k (for a large energy difference between LP and dark excitons), but still has kBT ~ ℏωα (for low-frequency acoustic phonon α), TAST predicts that there is no renormalization, and the current theory predicts that there will be a finite magnitude of renormalization (see Fig. 2D for T vg renormalization can be found in Fig. 3c in ref. 13. On the other hand, if one wants to choose the mechanistic interpretation based on Eq. (23), then our current theory will give a precise expression of how G should depend on temperature, which is \(G=({e}^{\beta \hslash \Delta {\omega }_{-k}}/{\tilde{v}}_{g,-})\frac{d}{d{k}_{\parallel }}\left[| {C}_{k}{| }^{2}{\sum }_{\alpha }2{c}_{\alpha }^{2}\cdot {\Xi }_{-k,0}({\omega }_{\alpha })\right]\), see details in Supplementary Note 5. In that sense, we view our current theory as a more general, microscopic one compared to TAST.
We developed a microscopic theory that successfully explains the renormalization of polariton group velocity due to polariton-phonon interactions. We analyze a theoretical model based on the GHTC Hamiltonian, which comprises N identical copies of molecular systems consisting of excitons and phonons that are collectively coupled to \({{{\mathcal{M}}}}\) cavity modes, which satisfy some dispersion relation. The theory uses a diagrammatic perturbative treatment of the equilibrium Green’s function of the polaritons, revealing how exciton-phonon interactions renormalize the LP band and thus reduce the group velocity in polariton transport. Crucially, the theory captures the λ and T dependence of the vg renormalization magnitude and semi-quantitatively agrees with results from quantum dynamics simulations. We emphasize that there is no free parameter in our microscopic theory, and every quantity is derived from the microscopic light-matter interaction Hamiltonian.
We expect the theory will eventually break down with increasing λ and matter fraction, such that the system enters into the non-perturbative regime. However, for λ ≤ kBT, the analytic theory almost quantitatively agrees with the numerical results. Although the theory does not capture transient non-equilibrium dynamical behaviors in the short-time regime, it yields semi-quantitatively accurate answers compared to numerical simulations that do include all transient non-equilibrium effects. This strongly suggests that the LP vg renormalization is largely dictated by the renormalization of the LP band due to phonons and is less sensitive to the transient dynamics.
Our theory yields several predictions regarding the scaling relation with matter fraction ∣Ck∣2, phonon bath reorganization energy λ, temperature, etc., and these have been verified through our quantum dynamics simulations. These predictions can, in principle, be verified with experiments3,4,6. The theory is simple enough to be extended to multidimensional systems with multiple dispersive matter bands and phonons, such as semiconductor materials. It is also feasible to implement our theory along with ab initio simulations33.