Black holes appear stranger and more bewildering the more deeply scientists study them. They display complex characteristics that defy simple explanations. One such characteristic is the vibrations they emit when perturbed.
When they’re perturbed, black holes ‘ring’ like a bell in distinctive patterns that physicists call Quasinormal Modes (QNMs). QNMs are damped oscillations that illustrate how black hole react to perturbations and eventually return to equilibrium. By studying QNMs, researchers hope to learn more gravitational wave astronomy and the complex physics of black holes.
When black holes merge, their QNMs are strong enough to detect from Earth. They’re a precious opportunity to learn more about a black hole’s mass and its shape. Measuring black hole masses is challenging, and to do so, researchers often rely on the orbital dynamics of stars that orbit them. QNMs are complex, and scientists define them as having both real and imaginary parts, if that makes sense. The real part determine the frequency of the oscillations, and the imaginary part determines the decay rate.
This artist’s illustration shows two black holes merging. The vibrations from the merger can reveal a lot about the black holes when the right methods are applied. Image Credit: NASA
QNMs contain fundamental information about black holes and depend only on their mass, charge, and angular momentum, not on their formation or how they were perturbed. However, precise calculations of these vibrations is challenging. Vibrations that are quickly weakening are especially challenging to calculate.
Researchers at Kyoto University in Japan attempted a new method of measuring them called the Wentzel–Kramers–Brillouin (WKB) method. Their work is in new research in Physical Review D, and it’s titled “Path to an exact WKB analysis of black hole quasinormal modes.” The lead author is Taiga Miyachi.
While WKB is used in mathematics, its application in physics and black hole research is still being developed. “To our knowledge, this is the first concrete application of the exact WKB analysis to the black hole perturbations,” the authors write in their paper.
“The foundations of the exact WKB method were largely developed by Japanese mathematicians. As a researcher from Japan, I have always found this field intellectually and culturally familiar,” said corresponding author Taiga Miyachi in a press release.
The researchers were able to follow the wave patterns in detail, even where other methods failed. They used Stokes curves to determine where the waves experience sudden changes. Stokes curves or Stokes lines mark boundaries in complex planes. Stokes curves can spiral infinitely and have paths that branch away from black holes, and previous researchers have overlooked them. But by incorporating them into their work, Miyachi and colleagues have revealed a black hole’s rich structure.
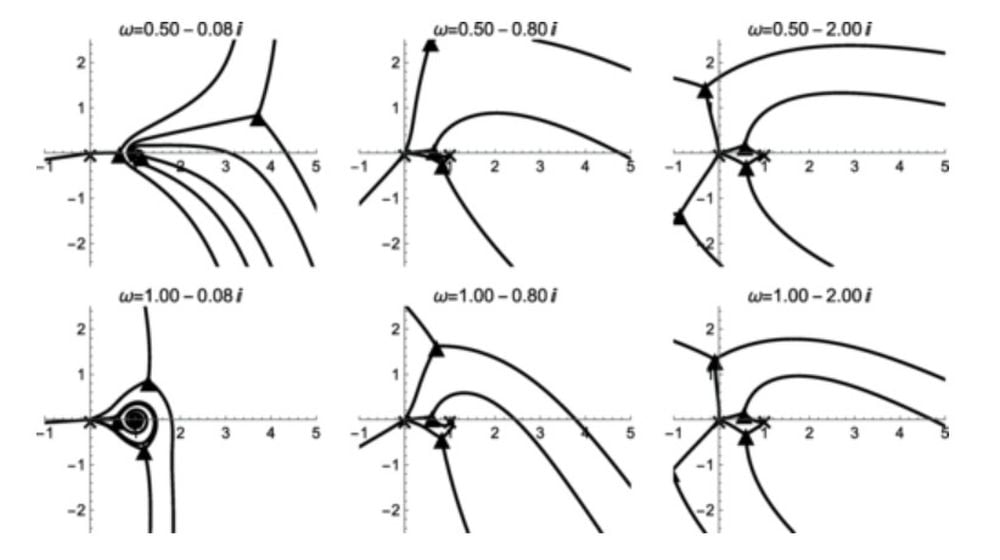This figure from the research shows some of the Stokes curves the researchers worked with. They’re representative of some of the values for QNM frequencies. Image Credit: Miyachi et al. 2025. Physical Review D.
“We were surprised at how complex and beautiful the underlying structure of these vibrations turned out to be. We found spiraling patterns in our mathematical analysis that had been missed before, and these turned out to be key in understanding the full picture of quasinormal modes,” said Miyachi.
In their paper’s conclusion the authors wrote, “In summary, the exact WKB analysis is a versatile and powerful tool for addressing black hole perturbation theories across a wide range of contexts.”
Most of us rely almost completely on words to describe Nature. But Galileo Galilei urged us to understand that mathematics is the language of Nature. In his 1623 work, Il Saggiatore (The Assayer), Galileo wrote:
“Philosophy is written in this grand book, the universe, which stands continually open to our gaze. But the book cannot be understood unless one first learns to comprehend the language and interpret the characters in which it is written. It is written in the language of mathematics, and its characters are triangles, circles, and other geometrical figures, without which it is humanly impossible to understand a single word of it; without these, one is wandering about in a dark labyrinth.”
Most of us will never understand the kind of complex mathematics used in this research. But we can understand its importance. It’s made it possible to analyze black hole vibrations and to learn more about these beguiling objects that are fundamental parts of Nature.
With this method, astrophysicists will be able to analyze the vibrations coming from perturbed black holes, especially merging ones. These analyses should improve the accuracy of our gravitational wave observatories and deepen our understanding of black holes.