FIMS/SPEAR data
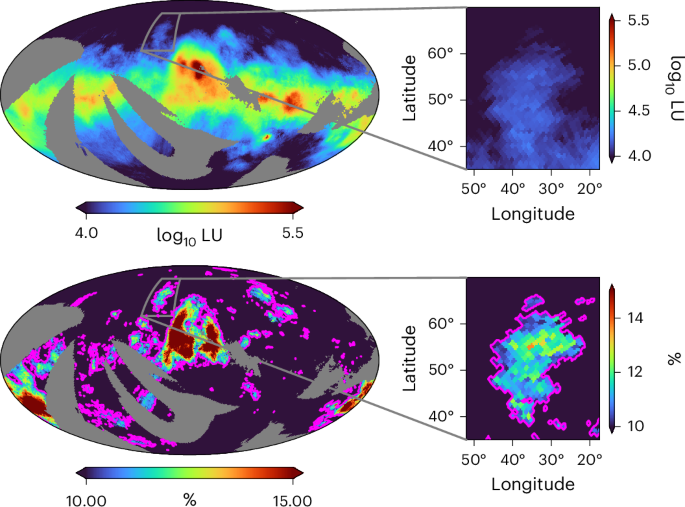
We briefly review the data collection and identification of the H2 lines. For this investigation, we have used data from the FIMS/SPEAR long-wavelength channel (L-channel; 1,350–1,710 Å), which includes several key transitions of molecular hydrogen fluorescence. While the spectral resolution of the data is too low for individual line identification, the collected data provides low-resolution H2 bumps within the L-channel spectrum that can be used to detect H2 fluorescence. The H2 fluorescence features are dominant in two bands, from 1,450 to 1,525 Å and from 1,560 to 1,630 Å. Reference 13 used data from the FIMS/SPEAR mission to construct a nearly all-sky map of diffuse molecular hydrogen fluorescence in emission, as well as an FUV continuum map.
The FIMS/SPEAR all-sky diffuse-background FUV spectrum, weighted by exposure time and with direct stellar photons excluded, consists of multiple components: dust-scattered stellar continuum, hydrogen two-photon continuum, extragalactic background continuum, atomic emission lines and H2 fluorescence emission lines. The spectrum includes atomic emission lines such as Si iv λ1403, Si ii* λ1533, C iv λλ1548, 1551, He ii λ1640 and Al ii λ1671, along with several quasi-bandlike features of H2 fluorescence emission lines. The H2 fluorescence features are most prominent in the wavelength ranges 1,450–1,525 Å and 1,560–1,630 Å. To improve the signal-to-noise ratio, the original data cube, with stellar photons removed, was rebinned to the larger wavelength bin size of 3 Å. As a result, the seven H2 fluorescence emission lines with significant peaks consist of many narrow lines and appear as broad lines in the coarse-grained spectrum. An example spectrum can be seen in Fig. 1 of ref. 13. The data are public on the NASA Mikulski Archive for Space Telescopes (MAST) archive.
To extract only the H2 fluorescence emission, ref. 13 removed all continuum background components and atomic emission lines. The H2 fluorescence emission map was constructed using a pixel size of approximately 0.92° (ref. 41). The spectrum for each pixel was obtained by smoothing the spectra of neighbouring pixels with weights proportional to the exposure time. The radius of the smoothing circle for each pixel was adaptively increased from 2° to 15° in steps of 1° until the signal-to-noise ratio per spectral bin was greater than 15. The Eos cloud is a robust feature of the data regardless of whether adaptive smoothing is utilized or not (Supplementary Fig. 1).
The origins of the H2 line emissionModelling the limited sensitivity of FIMS/SPEAR
The Eos cloud was discovered through H2 fluorescence lines, which were observed by FIMS/SPEAR during its all-sky survey. A variety of factors limited the instrument’s ability to capture all of the H2 fluorescence lines. The primary limitation is the instrument’s bandpass, which is unable to capture H2 lines below 1,350 Å. The spectral resolution and sensitivity of the instrument impose further limitations for the remaining in-band emission lines. From the H2 emission map and corresponding exposure time maps developed in ref. 13, the average exposure time per pixel is ~2,200 s for the Eos cloud. Due to contamination during launch operations, the L-channel sensitivity suffered a loss of ~74% (refs. 42,43). Given the relatively low exposure time, significant loss in sensitivity and low R ≈ 550, only a small fraction of the total intensity emitted in the H2 lines is detected. We define this fraction to be
$$\eta =\frac{\langle {{\mathcal{I}}}_{\det }\rangle }{{{\mathcal{I}}}_{{\rm{tot}}}}$$
(1)
where \({{\mathcal{I}}}_{{\rm{tot}}}\) is the total H2 line intensity emitted by the Eos cloud and \(\langle {{\mathcal{I}}}_{\det }\rangle\) is the H2 line intensity detected by FIMS/SPEAR, both in LU.
To determine the fraction η for the Eos cloud, we utilize the H2Spec model developed in ref. 44 to generate synthetic H2 spectra. H2Spec requires as inputs the column density of H2, the gas temperature of H2 and a source spectrum. We assume that the observed H2 is pumped by the Draine UV interstellar radiation field (ISRF)45, which is parameterized by the Draine field strength:
$$\chi =\frac{u}{{u}_{0}}$$
(2)
where u is the FUV energy density within a wavelength range of 912–2,480 Å and u0 is the FUV energy density of the Draine ISRF. A value of χ = 1 corresponds to a unit Draine field (which is equivalent to G0 = 1.7, where G0 is the field strength in units of the Habing field46). We use χ = 1 as the first model input, representative of the typical UV background for the solar neighbourhood45, along with an H2 gas temperature of T = 100 K. We also explored T = 500 K but found that this did not strongly affect the line amplitudes. We generate synthetic fluorescence spectra with H2Spec, where the H2 column density of the emitting layer is the sole variable. The value of \({{\mathcal{I}}}_{{\rm{tot}}}\) is then calculated for each synthetic spectrum.
To estimate \(\langle {{\mathcal{I}}}_{\det }\rangle\), we model the instrument’s response to the synthetic H2 fluorescence spectrum. We first convolve the synthetic spectrum with a line spread function consistent with a fully illuminated instrument slit. We then calculate the noise floor of a single FIMS/SPEAR observation of the Eos cloud by utilizing the 3σ instrument sensitivity curve as a function of wavelength, found in Fig. 1 of ref. 47. These sensitivities were calculated before FIMS/SPEAR was launched, and account for the ~74% loss in sensitivity in the instrument response model. We adjust the sensitivity curve to be consistent with the exposure time reported in the H2 exposure time map. Finally, the observed spectrum is interpolated onto the FIMS/SPEAR L-channel bandpass.
We combine the H2Spec model and the instrument response model to determine the value of η for the FIMS/SPEAR cloud. We fit the H2 column density to the observed range of \(\langle {{\mathcal{I}}}_{\det }\rangle\) values in the Eos cloud, \(\langle {{\mathcal{I}}}_{\det }\rangle =(1.29\pm 0.29)\times 1{0}^{4}\) LU. The best fit results in \({{\mathcal{I}}}_{{\rm{tot}}}=(1.44\pm 0.10)\times 1{0}^{5}\) LU. Therefore, the Eos cloud is observed to have η = (8.96 ± 2.11) × 10−2. For reference, the value obtained for the model assuming T = 500 K was η = (7.77 ± 1.11) × 10−2.
In the following sections, we compare the value of \({{\mathcal{I}}}_{{\rm{tot}}}\) with model predictions, first considering an analytic photodissociation region model that assumes chemical steady state and then considering an out-of-equilibrium model.
Chemical steady-state theoretical model
Following ref. 48, the total H2 line intensity in a steady-state photodissociation region is given by
$${{\mathcal{I}}}_{{\rm{tot}}}=\frac{Rn}{4\uppi {\sigma }_{\mathrm{g}}}\frac{1-{p}_{{\rm{diss}}}}{{p}_{{\rm{diss}}}}\ln \left(1+\frac{3\chi }{n/[10\,{{\rm{cm}}}^{-3}]}\right)\beta$$
(3)
$$=3.5\times 1{0}^{4}\,\left(\frac{n}{10\,{{\rm{cm}}}^{-3}}\right)\ln \left(1+\frac{3\chi }{n/[10\,{{\rm{cm}}}^{-3}]}\right)\,{\rm{LU}},$$
(4)
where \({{\mathcal{I}}}_{{\rm{tot}}}\) (LU) is the total line FUV intensity, R (cm3 s−1) is the H2 formation-rate coefficient on dust grains, n (cm−3) is the hydrogen nucleus number density (including H and H2), σg (cm2) is the dust absorption cross-section in the Lyman–Werner band per hydrogen nucleus, pdiss is the photodissociation probability per H2 photo-excitation, χ is the illuminating FUV radiation field intensity in units of the Draine field and β is a dimensionless factor accounting for the attenuation of H2 emission lines by dust (Appendix A in ref. 38).
This model assumes chemical steady state between H2 formation on dust grains and H2 photodissociation by Lyman–Werner radiation within an optically thick, uniform-density one-dimensional slab, externally irradiated by Lyman–Werner radiation normal to the slab surface. For a full derivation, see ref. 48 and Appendix A in ref. 38. We express Sternberg’s dimensionless parameter αG (characterizing the H2 dissociation-to-formation-rate ratio) in terms of the radiation-intensity-to-density ratio χ/n, assuming αG = 59χ/n cm3 for standard solar metallicity gas (see equation 22 in ref. 49).
In equation (4), we evaluate the expression assuming standard parameter values: pdiss = 0.15, R = 3 × 10−17 cm3 s−1, σg = 1.9 × 10−21 cm2 and β = 0.5 (ref. 38). Notably, \({{\mathcal{I}}}_{{\rm{tot}}}\) is only weakly sensitive to metallicity and dust-to-gas ratio variations, as both R and σg are proportional to the effective area of dust grains, causing their effects to largely cancel out in equation (4).
Supplementary Fig. 2 presents the theoretical prediction of \({{\mathcal{I}}}_{{\rm{tot}}}\) as a function of χ (blue curve) for n = 10 cm−3, as given by equation (4). The surrounding shaded region corresponds to models with densities varying from n = 1 cm−3 (lower envelope) to n = 100 cm−3 (upper envelope). The vertical magenta-shaded zone encloses expected values of χ = 0.5–1, representing a parameter space around the standard ISRF value χ = 1. The horizontal orange strip above the theoretical models represents the total H2 line intensity emitted by the Eos cloud found in the previous section.
Our analysis reveals that the chemical steady-state model predictions are below the observed total H2 line intensity emitted by the Eos cloud considering a typical UV ISRF. This discrepancy could be attributed to a combination of factors, including the impact of additional excitation sources, such as energetic photoelectrons produced by X-ray absorption, and the invalidity of the chemical steady-state assumption for the Eos cloud. Both factors are likely contributors, given the cloud’s proximity to the NPS/Loop I and its shape imprinted on the NPS/Loop I.
Non-steady-state model
Regarding out-of-equilibrium H2: as described in equation 9 of ref. 38, the observed H2 dissociation rate is given by
$${\dot{\varSigma }}_{\mathrm{D}}^{({\rm{obs}})}=0.3\,{{\mathcal{I}}}_{5}\left(\frac{{N}_{21}}{1-{{\rm{e}}}^{-1.9{N}_{21}}}\right)\,M_{\odot }\,{{\rm{pc}}}^{-2}\,{{\rm{Myr}}}^{-1},$$
(5)
where \({{\mathcal{I}}}_{{\rm{tot}}}\) is the total photon intensity summed over all the FUV emission lines (photons cm−2 s−1 sr−1) and \({{\mathcal{I}}}_{{\rm{5}}}\equiv {{\mathcal{I}}}_{{\rm{tot}}}/1{0}^{5}\,({\rm{photons}}\,{{\rm{cm}}}^{-2}\,{{\rm{s}}}^{-1}\,{{\rm{sr}}}^{-1})\), and N21 ≡ N/1021 (cm−2) is the average column density of atomic neutral hydrogen. With the estimated averaged \({{\mathcal{I}}}_{{\rm{tot}}}=1.4\times 1{0}^{5}\) LU from FIMS/SPEAR line modelling and average N21 ≈ 0.4 from GALFA, we obtain \({\dot{\varSigma }}_{\mathrm{D}}^{({\rm{obs}})}=0.32\,M_{\odot }\,{{\rm{pc}}}^{-2}\,{{\rm{Myr}}}^{-1}\).
Similarly, equation 12 of ref. 38 provides an estimate of the formation rate (\({\dot{\varSigma }}_{\mathrm{F}}^{({\rm{obs}})}\)), with this power-law relation:
$${\dot{\varSigma }}_{\mathrm{F}}^{({\rm{obs}})}=0.14\,{f}_{{\rm{H}}}{N}_{21}^{1+\alpha }\,M_{\odot }\,{{\rm{pc}}}^{-2}\,{{\rm{Myr}}}^{-1},$$
(6)
where α = 1.3 and fH ≡ N(H)/N. The power-law relation with N21 arises from calibration using numerical simulations50,51 to approximate the product of the formation-rate coefficient of H2 on dust grains and the ISM density. More discussion on the derivation of equation (6) can be found in ref. 38. For the Eos cloud, the estimated formation rate using fH = 1 and the average N21 ≈ 0.4 from GALFA is \({\dot{\varSigma }}_{\mathrm{F}}^{({\rm{obs}})}=0.02\,M_{\odot }\,{{\rm{pc}}}^{-2}\,{{\rm{Myr}}}^{-1}\).
These calculations suggest that photodissociation (from X-rays and UV) dominates H2 formation for this cloud. Future studies using spectral resolution higher than that of FIMS/SPEAR could directly test how far the cloud is from chemical equilibrium37.
All-sky maps of O vi, CO and X-ray data
All-sky maps showing the O vi, CO and X-ray data are provided in Fig. 4 to give context to the location of the cloud on the sky in various tracers. In particular, in addition to the ROSAT soft-X-ray data, the Eos cloud can be seen as a foreground shadow to other hot gas tracers. In the top panel of Fig. 4, we show the cloud contours overlaid on an all-sky map of five-times ionized oxygen (O vi) published in ref. 52. O vi traces hot, ionized regions probably produced by supernova remnants in the ISM with temperatures around a million degrees Kelvin. The cloud discussed herein produces a characteristic absorption in the O vi emission map, similar to what is shown by the soft-X-ray data, indicating that it is a cooler, denser foreground object. We note that the exact shape of the structures in these emission maps depends on where the hot gas causing the O vi ions originates and can include geometric effects of the line of sight and magnetic field. O vi absorption to stars with known distances will be of great value in understanding the relation between the hot gas and the Eos cloud. On the basis of the spatial correspondence between the X-ray data, O vi emission map and Eos cloud, it is very likely that this interaction between the molecular complex and hot gas provides the nearest example of a hot–cold ISM gas interface, which is also thought to be responsible for the O vi absorption observed through many sight lines throughout the Galaxy.
Jeans stability
Given the presence of even a small mass of cold CO-bright gas, it is natural to enquire about the fate of this diffuse high-latitude molecular cloud. Is it on its way to being actively star forming, as is the case of present-day, more massive molecular clouds in the Local Bubble vicinity? Or will the cloud photodissociate before star formation can take place? Using a range of cloud masses and temperatures, we can estimate the Jeans mass of the cloud, assuming a radius of 25.54 pc (estimated using the dust-based distance to the cloud and size on the sky). Masses larger than the Jeans mass are unstable to gravitational contraction, which occurs when the gravitational free-fall timescale is shorter than the sound-crossing timescale.
Supplementary Fig. 3 shows the ratio of the cloud mass to the Jeans mass, considering only thermal support. For a range of estimated masses from 3D dust maps (Supplementary Fig. 4) and over a range of reasonable temperatures for the H2 gas, the cloud is marginally stable against gravitational collapse for temperatures above 100 K. This reflects the very low densities of the diffuse gas of ρ = 0.08 M⊙ pc−3. We note that our calculations make simplistic assumptions about spherical geometry and lack estimations for turbulence and magnetic fields. However, adding these terms would only strengthen the support of the cloud against collapse. Future work will examine the role of turbulence and magnetic fields in the Eos cloud with additional analysis of 21-cm emission maps and Planck polarization data.
Building the 3D dust density map
We compute a 3D dust map of the solar neighbourhood out to a distance of 350 pc using the 3D dust mapping algorithm Dustribution23,24,25 modified with a variational nearest-neighbour Gaussian process53. Variational nearest-neighbour Gaussian processes can scale to almost unlimited numbers of voxels in the map in linear, rather than cubic, time; these modifications will be described in more detail in a forthcoming paper. This volume is divided into voxels such that (nl, nb, nd) = (360, 180, 117) with equal spacing in l and d and in sin b, giving us a grid resolution of l, b, d = 1°, 1°, 3 pc.
Dustribution takes in any catalogue of 3D dust extinction and distances and computes its 3D dust density and extinction within the given region. For the purposes of this Article, we utilize the catalogue of ref. 54, which derives stellar parameters from Gaia Data Release 3 BP/RP spectra, BP/RP and G photometry and parallaxes, 2MASS and Wide-field Infrared Survey Explorer photometry and LAMOST spectra using a data-driven approach.
To derive the 3D isocontour from Astrodendro requires several input parameters: the minimum density above which cells may be included in structures, the minimum difference at which substructures may be identified and the minimum number of pixels in a structure, which we set to 4 × 10−5 mag pc−1, 0.15 dex and 8 pixels, respectively, on the basis of the final mean Dustribution model parameters.
For validation, we compare the Eos cloud line-of-sight width and masses with those of ref. 55. Applying the above methods to determine distance and mass, we derive a line-of-sight distance of 90–140 pc and a mass of 1.6 × 103 M⊙. While the line-of-sight width is in excellent agreement with our results from Dustribution, there is a difference of approximately a factor of 3 in the recovered masses. This mass discrepancy could be a result of the differences in the implementation and the resolutions of the two 3D dust density maps.
CO mass
Several large and well-known molecular complexes in the Local Bubble vicinity are actively star forming, including Taurus, Ophiuchus, Lupus, Chamaeleon and Corona Australis1. These clouds are all observed in dense and cold gas tracers such as CO. In Fig. 4, second row, we show the CO data from ref. 6. As previously mentioned, a small CO cloud (MBM 40) is present at l = 37.75° and b = 44.75°.
While the distance to MBM 40 is not well constrained, if it is associated with the Eos cloud we can compute its mass, given the known distance to Eos. Adopting a CO-to-H2 conversion factor of 2 × 1020 cm−2 (K km s−1)−1 (ref. 56) and including a factor of 1.36 for heavy elements, we can compute the cloud mass from the CO luminosity:
$$M\,({M}_{\odot })=0.0013{L}_{\mathrm{CO}}\,\left({\mathrm{K}}\,{\mathrm{km}}\,{\mathrm{s}}^{-1}\,{\text{deg}}^{2}\right)\,[d\,{(\text{pc})}]^{2}.$$
(7)
Using LCO = 1.53 K km s−1 deg2 from ref. 6 and d = 100 pc, the mass of the Eos cloud predicted by the CO emission is estimated to be M = 19.9 M⊙. Variations of a factor of a few in mass may be expected due to uncertainties in the CO-to-H2 conversion factor at high Galactic latitudes22,57. The CO luminosity estimates a cloud mass that is two to three orders of magnitude off of the mass estimated from dust and traces a much smaller volume than the more diffuse H2 gas. This highlights the importance of tracking CO-dark gas when estimating cloud masses and extents.