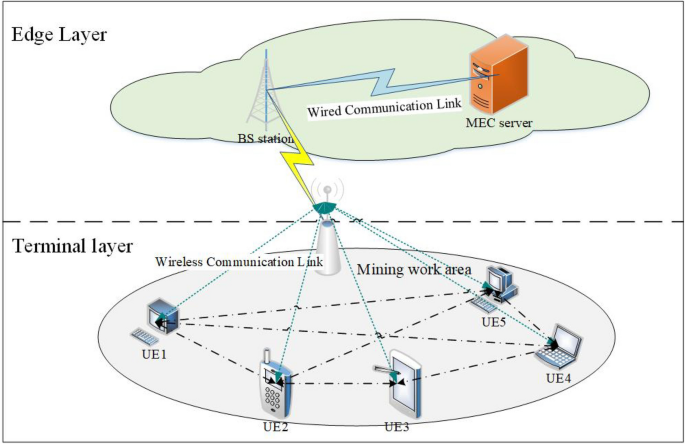
In this section, we present experimental validation and discussion of the proposed IGA-DDPG algorithm. Consider a mining edge computing scenario with a mining working face area of 600\(\times\)600 square meters. In this area, an MEC server and a communication base station are deployed, with mobile terminal devices randomly distributed throughout the mine. The available bandwidth resources are divided into 90 subchannel bands. Based on the described physical interference model, the channel gain is set as \(h = d^{-4}\), where \(d\) represents the propagation distance53. Experiments were conducted on the MATLAB 2020b simulation platform to verify the effectiveness of the proposed IGA-DDPG algorithm. The key parameters for system simulation are listed in Table 3.
Table 3 Parameter settings table.
We compare the IGA-DDPG proposed in this paper with the following five task offloading benchmark schemes:
-
IGWO ( Improved Grey Wolf Optimizer metaheuristic algorithm): This algorithm is an enhanced version of the Grey Wolf Optimizer (GWO) that incorporates a nonlinear convergence factor and dynamic weighting. It is selected because it represents a swarm intelligence-based heuristic optimization approach that has been widely applied in task scheduling and resource allocation problems. Comparing IGA-DDPG with IGWO helps evaluate the effectiveness of reinforcement learning (RL) in optimizing offloading strategies.
-
TGA (Traditional Genetic Algorithm Optimization): The traditionalThe genetic algorithm is a widely used evolutionary optimization technique. TGA is chosen as a baseline because, like IGA-DDPG, it is an evolutionary optimization method, albeit without reinforcement learning integration. This comparison allows us to assess the advantages of combining genetic algorithms with deep reinforcement learning in complex offloading scenarios.
-
BODM (Binary Offloading Decision Mechanism): This method follows a binary offloading approach, where tasks are either fully executed locally or offloaded to an MEC server. BODM is included as a baseline to compare against methods that allow more flexible task partitioning and collaborative computing, such as IGA-DDPG, which enables fine-grained offloading decisions.
-
PNCM (Partially Non-Cooperative Mechanism): In this scheme, tasks can be executed locally or offloaded to the MEC server, but they cannot be offloaded to other service terminals. PNCM represents a semi-collaborative offloading model, making it an appropriate baseline to compare against the cooperative task execution capabilities of IGA-DDPG.
-
FLEM (Fully Local Execution Mechanism): This scheme represents the most basic execution strategy, where all computational tasks are performed locally on the user device. FLEM serves as an essential baseline to highlight the benefits of offloading strategies, particularly in terms of reduced computation time and system cost.
Time complexity and space complexity evaluation
In Table 4,By comparing the time and space complexity, IGA-DDPG demonstrates optimal computational efficiency and storage requirements, with a time complexity of \(O(GPN) + O(EBN)\) and a space complexity of \(O(GP + EB)\). This enables efficient resource scheduling and dynamic optimization in large-scale MEC task offloading scenarios. In contrast, IGWO is suitable for medium-scale task offloading; however, due to its broader optimization search space, its computational complexity, \(O(IN^2)\), remains higher than that of IGA-DDPG. TGA has the highest computational complexity, reaching \(O(GPN)\). Due to its population evolution mechanism, its optimization speed is relatively slow, making it unsuitable for large-scale MEC tasks. BODM and PNCM exhibit relatively lower computational complexity, with \(O(N\log N)\) and \(O(N^2)\), respectively, making them suitable for small-scale task offloading scenarios. However, they still have limitations in dynamic resource optimization. FLEM, which relies entirely on local computation, has the lowest time complexity of \(O(N)\), but suffers from poor task processing efficiency, making it inadequate for MEC computing demands. Overall, IGA-DDPG integrates genetic algorithms and deep reinforcement learning, achieving efficient task scheduling optimization while maintaining low computational complexity. Compared to traditional algorithms, IGA-DDPG outperforms in terms of computational complexity, storage consumption, and task scheduling efficiency.
Table 4 Parameter settings table.Comparative analysis of IGA-DDPG, IGA, and DDPG
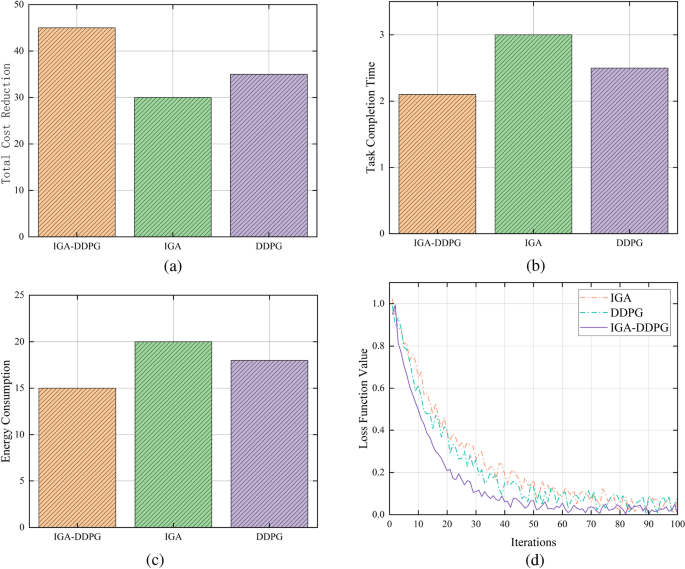
This section compares the performance of the IGA-DDPG, IGA, and DDPG algorithms based on total cost reduction, task completion time, and energy consumption. The experimental results are presented in Fig. 2. As shown in Fig. 2a, IGA-DDPG achieves the highest total cost reduction, significantly outperforming both IGA and DDPG. The total cost reduction for IGA-DDPG is 45%, whereas IGA and DDPG achieve only 30% and 35%, respectively. This indicates that IGA-DDPG provides a more effective trade-off between energy efficiency and computational performance, demonstrating its superior optimization capabilities in complex task offloading environments.
Comparative analysis of IGA-DDPG, IGA, and DDPG.
Figure 2b illustrates the task completion time for the three algorithms. The IGA-DDPG algorithm achieves the lowest task completion time of 2.1 seconds, significantly outperforming DDPG (2.5 s) and IGA (3.0 s). The shorter completion time indicates that IGA-DDPG effectively optimizes task scheduling and resource allocation, reducing system latency while maintaining a balanced computational load. In contrast, IGA and DDPG experience higher delays due to suboptimal exploration-exploitation balancing and less efficient convergence behavior.
Figure 2c presents the energy consumption of each algorithm. IGA-DDPG consumes the least energy at 15J, while DDPG and IGA consume 18J and 20J, respectively. The lower energy consumption of IGA-DDPG highlights its enhanced power efficiency, which is critical for resource-constrained edge computing environments. The higher energy consumption of IGA and DDPG indicates less efficient decision-making, leading to increased computational overhead and unnecessary processing cycles.
Figure 2d shows the loss function value over iterations. The IGA-DDPG algorithm achieves the fastest and most stable convergence, with the lowest loss values across all iterations. The improved convergence speed of IGA-DDPG compared to IGA and DDPG indicates its ability to rapidly learn optimal task offloading policies, leading to more efficient and adaptive performance. IGA and DDPG exhibit slower convergence and higher loss fluctuations, suggesting greater instability and suboptimal parameter updates during the training process.
Impact analysis of the number of mining terminals
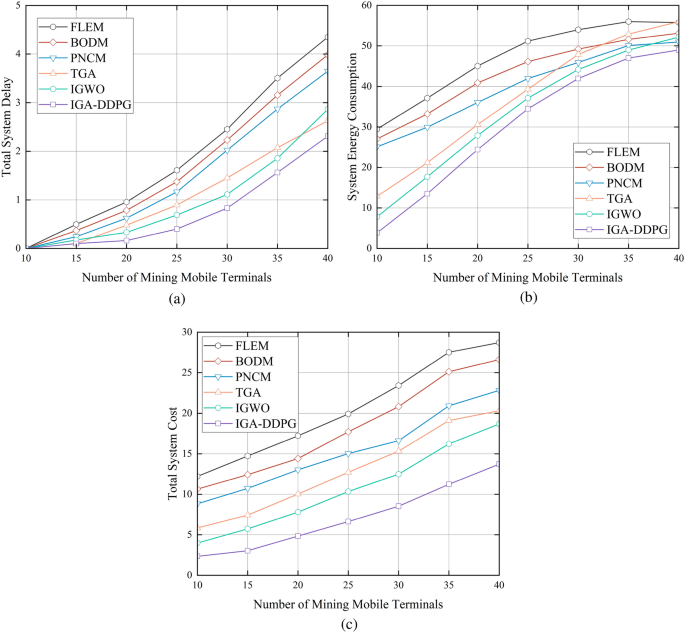
This section compares the performance of the proposed IGA-DDPG algorithm with five baseline algorithms under different numbers of mining mobile terminals. The number of terminals is gradually increased from 10 to 40, and the evaluation focuses on total system delay, energy consumption, and total system cost.
Figure 3a presents the total system delay of different algorithms. When the number of terminals is fewer than 15, system delay remains nearly zero across all algorithms. This is because most tasks are executed locally, reducing the need for task offloading, which would otherwise introduce additional transmission and computation delays. However, as the number of terminals increases beyond 20, offloading becomes necessary due to resource limitations, causing a significant rise in system delay across all algorithms.Among the tested algorithms, IGA-DDPG exhibits the lowest system delay across all terminal sizes due to its optimized task allocation and dynamic offloading strategy. FLEM consistently shows the highest system delay, as it lacks offloading capabilities, resulting in severe local resource congestion. BODM and PNCM perform better than FLEM but experience sharp increases in delay when the number of terminals exceeds 25, indicating poor scalability. IGWO and TGA achieve moderate results, but their delay values still significantly exceed those of IGA-DDPG. On average, IGA-DDPG reduces system delay by 67.7%, 63.0%, 56.6%, 33.5%, and 29.5% compared to FLEM, BODM, PNCM, TGA, and IGWO, respectively.
Performance comparison of task offloading strategies under different numbers of terminals.
Figure 3b illustrates the total energy consumption for task offloading. Regardless of terminal scale-whether small-scale (10-20 terminals) or high-load (30-40 terminals)-IGA-DDPG consistently achieves the lowest energy consumption among all algorithms. As the number of terminals increases, the energy consumption of other algorithms rises significantly, whereas IGA-DDPG demonstrates a more stable growth trend, ensuring both lower absolute energy consumption and a smaller growth rate.Although TGA exhibits relatively low energy consumption for small-scale scenarios (10-15 terminals), its energy consumption increases rapidly when the number of terminals reaches 35 or 40, becoming one of the highest among all algorithms. FLEM incurs the highest energy consumption due to inefficient local execution, followed by BODM and PNCM, which also exhibit steep energy growth due to suboptimal task allocation strategies. IGWO performs better than BODM and PNCM but still lags behind IGA-DDPG in terms of energy efficiency. On average, IGA-DDPG reduces system energy consumption by 39.9%, 34.5%, 29.7%, 24.9%, and 18.1% compared to FLEM, BODM, PNCM, TGA, and IGWO, respectively.
Figure 3c presents the total system cost across different numbers of mining terminals. The total system cost is calculated based on a weighted combination of system delay and energy consumption, providing a comprehensive assessment of the efficiency of each algorithm. Across all tested terminal sizes, IGA-DDPG consistently achieves the lowest system cost, demonstrating its superiority in balancing multiple objectives. As the number of terminals increases, FLEM exhibits the highest total cost, primarily due to its high system delay and excessive energy consumption. **BODM and PNCM initially perform well but experience rapid cost escalation beyond 25 terminals, indicating that they are less effective in large-scale deployment scenarios. TGA and IGWO demonstrate relatively moderate cost increases, but they still accumulate significantly higher costs than IGA-DDPG as terminal numbers grow. Overall, IGA-DDPG achieves a more effective global trade-off in multi-objective optimization scheduling, making it the most cost-efficient solution among all tested algorithms. On average, IGA-DDPG reduces total system cost by 67.7%, 63.6%, 57.0%, 48.1%, and 29.8% compared to FLEM, BODM, PNCM, TGA, and IGWO, respectively.
Impact analysis of task data size
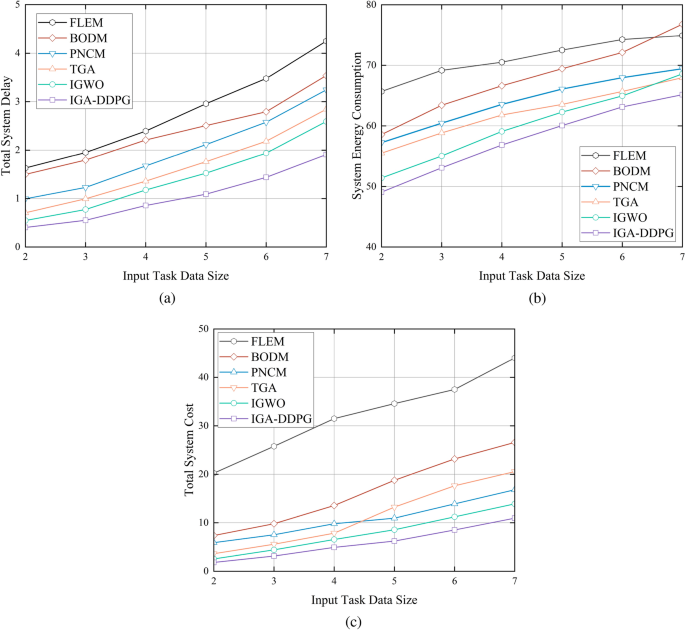
This section compares the performance of the proposed IGA-DDPG algorithm with five baseline algorithms under different computational task models. The input data size is gradually increased from 2 Mb to 7 Mb, and the evaluation focuses on system delay, energy consumption, and total system cost.
Figure 4a presents the total system delay for different input task data sizes. As the task data size increases from 2 Mb to 7 Mb, the system delay of all algorithms gradually increases, indicating that task data size is a direct influencing factor on system delay. The performance differences between the algorithms are significant. IGA-DDPG consistently outperforms all other algorithms with the lowest system delay, demonstrating its superior task offloading and scheduling efficiency. FLEM performs the worst, as all tasks are executed locally, leading to a severe increase in processing time and congestion. BODM and PNCM show better performance than FLEM but experience sharp increases in delay for larger task sizes, revealing their limitations in large-scale task handling. IGWO and TGA achieve moderate results, but their delay values remain significantly higher than those of IGA-DDPG. On average, IGA-DDPG reduces system delay by 64.6%, 59.1%, 49.4%, 38.2%, and 26.1% compared to FLEM, BODM, PNCM, TGA, and IGWO, respectively.
Performance of task offloading strategies under different input data sizes.
Figure 4b illustrates the total energy consumption for task offloading. As the input task data size increases from 2 Mb to 7 Mb, the energy consumption of all algorithms rises accordingly. However, IGA-DDPG consistently maintains the lowest energy consumption, with a relatively controlled increase even at high data sizes. This demonstrates the adaptive and global optimization capabilities of IGA-DDPG, making it more competitive in mining edge computing systems under surging traffic. It provides an efficient solution for achieving low energy consumption under high loads.Although TGA exhibits relatively low energy consumption for smaller task sizes, it undergoes a sharp increase when the task data size exceeds 5 Mb, making it one of the least energy-efficient algorithms. FLEM has the highest energy consumption, due to its inefficiency in local task execution, followed by BODM and PNCM, which also show steep energy growth due to suboptimal task allocation strategies. IGWO performs better than BODM and PNCM but remains less energy-efficient compared to IGA-DDPG.On average, IGA-DDPG reduces system energy consumption by 18.8%, 14.7%, 9.9%, 7.2%, and 5.4% compared to FLEM, BODM, PNCM, TGA, and IGWO, respectively.
Figure 4c presents the total system cost for different input task data sizes. The total system cost is calculated based on a weighted combination of system delay and energy consumption, providing a comprehensive evaluation of overall system efficiency. Across all tested task data sizes, IGA-DDPG consistently achieves the lowest total cost, demonstrating its effectiveness in balancing multiple optimization objectives.As the task data size increases, FLEM incurs the highest total cost, primarily due to its high system delay and excessive energy consumption. BODM and PNCM initially perform well but experience rapid cost escalation when the task data size exceeds 5 Mb, indicating their poor scalability. TGA and IGWO demonstrate relatively moderate cost increases, but their total cost still remains significantly higher than that of IGA-DDPG.Overall, IGA-DDPG achieves the most controlled growth in total system cost, proving its efficiency in reducing overall operational expenses. On average, IGA-DDPG reduces total system cost by 82.9%, 66.0%, 49.3%, 47.1%, and 33.6% compared to FLEM, BODM, PNCM, TGA, and IGWO, respectively.
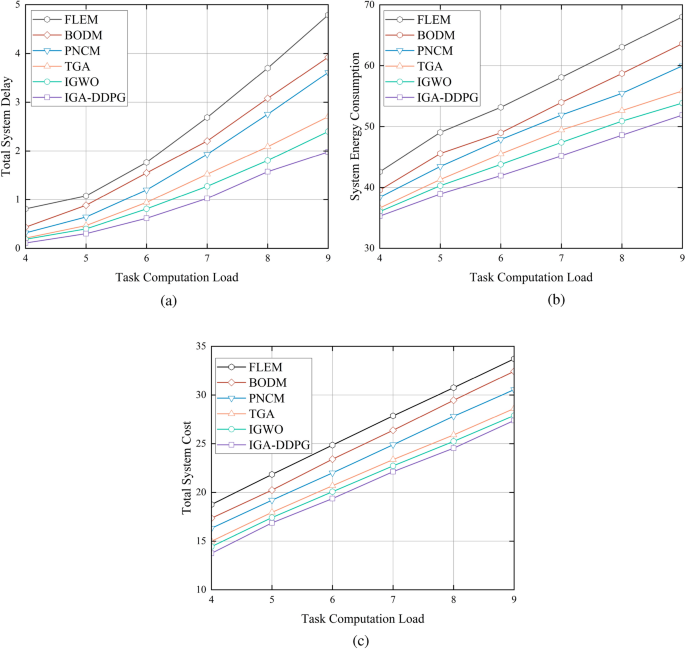
Impact analysis of the task computation load model
This section compares the performance of the proposed IGA-DDPG algorithm with five baseline algorithms under different computational task models. The task computation load is gradually increased from 4 GHz to 9 GHz, and the evaluation focuses on system delay, energy consumption, and total system cost.
Figure 5a presents the total system delay for different task computation loads. It can be observed that as the computation load increases from 4 GHz to 9 GHz, IGA-DDPG consistently achieves the lowest system delay and exhibits the most gradual increase among all algorithms.At the highest load of 9 GHz, the delay of IGA-DDPG is only approximately 1.98 seconds, whereas the delays of other algorithms range from 2.7 to 4.8 seconds, indicating that IGA-DDPG maintains superior efficiency under increasing workloads. FLEM exhibits the highest system delay, as it lacks offloading capabilities, leading to severe local computation congestion. BODM and PNCM show better performance than FLEM but experience sharp increases in delay as computation load increases, indicating their poor scalability. IGWO and TGA perform moderately well, but their delays remain significantly higher than those of IGA-DDPG. On average, IGA-DDPG reduces total system delay by 67.8%, 58.8%, 50.3%, 33.6%, and 17.4% compared to FLEM, BODM, PNCM, TGA, and IGWO, respectively.
Performance of task offloading strategies under different computational loads.
Figure 5b illustrates the total energy consumption for task offloading. As the computation load increases from 4 GHz to 9 GHz, the energy consumption of all algorithms rises significantly. This corresponds to the increased resource consumption, higher network communication, and heavier processing loads associated with greater computational demands.As the computation load increases, the performance advantage of IGA-DDPG becomes increasingly pronounced compared to traditional algorithms such as FLEM and BODM. Moreover, IGA-DDPG maintains a stable low-energy consumption gap compared to TGA and PNCM, ensuring energy-efficient performance across different computation loads.On average, IGA-DDPG reduces total system energy consumption by 21.3%, 15.3%, 11.6%, 6.8%, and 4.1% compared to FLEM, BODM, PNCM, TGA, and IGWO, respectively.
Figure 5c presents the total system cost for different task computation loads. From 4 GHz to 9 GHz, the total system cost for all algorithms increases monotonically. However, IGA-DDPG consistently maintains the lowest total cost across all computation loads, demonstrating its effectiveness in balancing energy efficiency and task delay optimization.As computation load increases, the total cost curves for BODM and PNCM become steeper, indicating their poor adaptability to higher workloads. Although TGA performs relatively well among traditional methods, its delay results suggest that IGA-DDPG maintains a significant advantage across all computation loads. IGWO also performs better than BODM and PNCM but remains suboptimal compared to IGA-DDPG.On average, IGA-DDPG reduces the total system cost by 21.4%, 17.6%, 12.8%, 6.3%, and 3.9% compared to FLEM, BODM, PNCM, TGA, and IGWO, respectively.
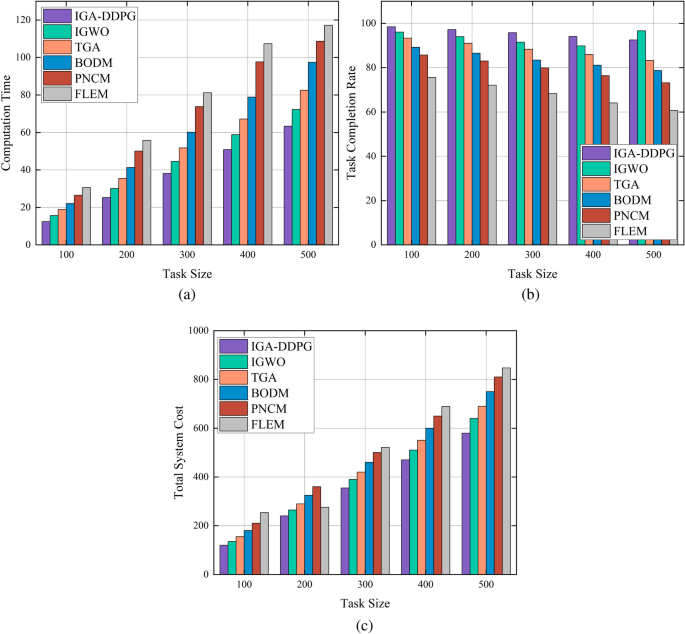
Performance analysis in large-scale scenarios
This section compares the performance of the proposed IGA-DDPG algorithm with five benchmark algorithms under different task scales. The task scale increases from 100 to 500, and the evaluation metrics include computation time, task completion rate, and total system cost.
Figure 6a illustrates the computation time of different algorithms. As the task scale increases, the computation time for all algorithms grows, indicating that task complexity directly affects computational overhead. IGA-DDPG consistently maintains the lowest computation time across all task scales, demonstrating superior computational efficiency. IGWO and TGA exhibit moderate computation time but are significantly higher than IGA-DDPG. In contrast, BODM and PNCM experience the fastest increase in computation time due to their exhaustive search strategies, leading to a sharp rise in computational burden for large-scale tasks. FLEM has the highest computation time, as all tasks are executed locally, resulting in severe computational bottlenecks. On average, IGA-DDPG reduces computation time by 49.2%, 43.9%, 35.2%, 28.1%, and 21.4% compared to FLEM, PNCM, BODM, TGA, and IGWO, respectively.
Performance of task offloading strategies in large-scale scenarios.
Figure 6b presents the task completion rate of different algorithms. As the task scale increases, the task completion rate of all algorithms declines due to resource constraints. However, IGA-DDPG consistently achieves the highest task completion rate, ranging from 98.5% to 92.5%, ensuring reliable task execution even under high computational loads. IGWO and TGA exhibit slightly lower task completion rates, ranging from 96.1% to 89.8% and 93.4% to 83.2%, respectively. In contrast, BODM and PNCM experience a more rapid decline, dropping to 78.7% and 73.2% at the largest task scale, indicating weaker adaptability under high-load scenarios. FLEM has the lowest task completion rate, reaching only 60.7%, as it fully relies on local computation, resulting in excessive task processing delays and an increased task failure rate. On average, IGA-DDPG improves the task completion rate by 52.2%, 47.1%, 36.2%, 27.4%, and 19.7% compared to FLEM, PNCM, BODM, TGA, and IGWO, respectively.
Figure 6c illustrates the total system cost, which includes computational resource consumption and execution latency. As the task scale increases, the total system cost rises for all algorithms. Due to its adaptive optimization strategy, IGA-DDPG achieves the lowest total cost across all task scales. IGWO and TGA exhibit moderate system costs, but their costs increase more rapidly as the task scale grows. BODM and PNCM experience a sharp rise in system cost when the task scale exceeds 300, reflecting their high computational overhead in large-scale task environments. FLEM consistently incurs the highest system cost, as all tasks are executed locally, leading to excessive computational resource consumption and a lower task completion rate, which further increases the overall system cost. On average, IGA-DDPG reduces the total system cost by 31.5%, 28.9%, 23.7%, 18.5%, and 12.3% compared to FLEM, PNCM, BODM, TGA, and IGWO, respectively.
Analysis of variance (ANOVA)
To assess whether the performance differences among the compared algorithms are statistically significant, we adopted the ANOVA-based experimental methodology employed in53.
Based on the results of one-way analysis of variance (ANOVA), we conducted significance tests on three key performance indicators: latency, energy consumption, and total cost. As shown in Table 5, the p-values for all three metrics are significantly lower than the significance level of \(\alpha = 0.05\), specifically \(9.0100 \times 10^{-5}\), 0.0194, and \(7.6803 \times 10^{-8}\), respectively. These results indicate that there are statistically significant differences in the performance of different algorithms across all evaluated metrics.
Table 5 Analysis of variance.