The flat bands of magic-angle twisted bilayer graphene1 (MATBG) offer a rich playground for condensed matter physics, as they host both strong electronic interactions and non-trivial topology2. A variety of symmetry-breaking ground states emerge at non-zero integer fillings of the moiré unit cell ν, where ν = 4n/ns and ns is the carrier density in a fully occupied moiré band. The contrasting properties of its ground states (which include superconductivity3,4,5, Mott-like physics4,6 and topological states7,8,9,10) suggest the coexistence of itinerant and localized electrons within the flat bands. In addition, the sawtooth-like evolution of the electronic entropy11,12,13,14,15 around integer ν, as well as the presence of Landau fans that only disperse away from the charge neutrality point (CNP)3,4,5,6, point to a distinct asymmetry of the charge ± 1 excitations of the symmetry-broken ground states.
Thermoelectric transport, parameterized by the Seebeck coefficient (S), constitutes an accurate probe of Fermi surface properties of condensed matter systems. In particular, S is highly sensitive to the band dispersion and the scattering mechanisms near the Fermi level EF. Generally, the sign and magnitude of S contain information about the charge of the majority carriers and their effective masses, as described by the semiclassical Mott relation16 (SMR) \({S}_{{\mathrm{Mott}}}\propto -T\frac{\partial }{\partial \mu }\mathrm{ln}\,\sigma \left(\,\mu \right)\), where T, μ and σ are the temperature, chemical potential and conductivity, respectively. In strongly correlated systems, such as cuprate superconductors17,18,19, heavy fermion compounds20,21 or narrow gap semiconductors22,23,24,25, deviations from the SMR can arise due to the coexistence of contrasting electronic orbitals21,25, reconstructing Fermi surfaces17,18 and the finite lifetimes of incoherent electron excitations19,24.
The thermoelectricity in the MATBG flat bands has been shown to violate the SMR26,27,28. Previous works reported no sign changes in S at integer fillings, where σ(μ) peaks, and observed a nonlinear temperature dependence where S does not extrapolate to zero in the limit of T → 0. This non-semiclassical thermoelectric response was attributed to electron–hole (e–h) asymmetry in the density of states of the flat bands. However, these studies used MATBG samples that lacked well-developed, symmetry-broken correlated states, which are predicted to be e–h asymmetric29,30,31,32,33. These findings were modelled using weakly interacting frameworks based on the SMR. Crucially, the SMR is not applicable to the MATBG flat bands, because it assumes rigid band filling. In addition, it neglects effects such as band-dependent scattering rates, which can substantially alter thermoelectric transport34.
In this Article, we explore the low-temperature thermoelectricity of the MATBG flat bands through optical excitation of gate-defined p–n junctions. We find strong evidence of photo-thermoelectric (PTE) voltage generation driven by the Seebeck effect in the MATBG flat bands. The PTE response develops oscillations at each integer filling, which arise from the formation of symmetry-broken correlated states. The thermoelectricity remains electron-like for positive fillings of the flat bands, despite interaction-induced reconstructions of the charge-one excitation bands and the opening of gaps around integer fillings. This observation points to a scenario in which electrons with long transport lifetimes dominate the thermoelectric transport over incoherent hole-like excitations. We provide a natural interpretation via the topological heavy fermion (THF) mapping of MATBG35,36, where the contrasting properties of light and heavy electrons37 inherently account for the observed response. We also study the high-temperature thermoelectricity of the flat bands, finding signatures of the persistent influence of strong electron correlations, even in the absence of symmetry-breaking ordered states.
We probed the low-temperature thermoelectric transport of the flat bands using laser excitation (at wavelength λ = 1,550 nm) to locally heat up a MATBG p–n junction, as sketched in Fig. 1a. We focused on two high-quality MATBG samples (with twist angles θ = 1.14° and θ = 1.06°) that exhibit well-developed correlated resistive states at non-zero ν (Fig. 1b), as well as superconducting phases (Supplementary Information). We note that both devices feature large activation gaps at half-filling (Δ+2 ≈ 1.9 meV), demonstrating the presence of strong electronic interactions. A gate-defined p–n junction was created by splitting the top graphite gate, allowing independent control of the carrier concentration on each side. The junction was defined in a section of the Hall bar device with a homogeneous twist angle near 1.1°. Figure 1c depicts the dual top-gate map of the junction’s longitudinal resistance (Rxx), where both sides of the junction feature pronounced correlated states that can be addressed independently.
Fig. 1: PTE effect in a gate-defined MATBG p–n junction.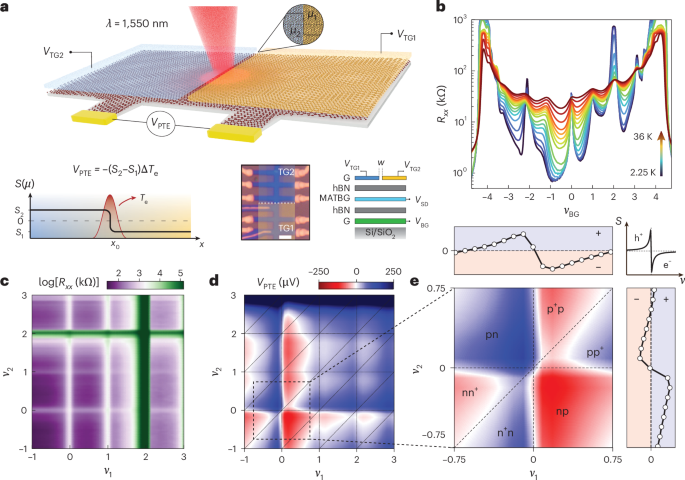
a, A local thermal gradient is created at the interface of a MATBG p–n junction using a focused laser beam. The gate-defined step in μ enables the generation of VPTE across the junction. VTG1 and VTG2, top-gate voltages; hBN, hexagonal boron nitride. Insets: origin of VPTE (left; x0 denotes the junction position), an optical micrograph of the sample (middle) and a schematic cross-section of the heterostructure (right; VBG, back-gate voltage; VSD, source–drain voltage for the transport measurements; w, junction width; G, few-layer graphite used as top and back gates.). b, Temperature-dependent four-terminal resistance of Device 1 (θ = 1.14°) before splitting the top gate at 2.25, 2.8, 3.6, 5, 6.5, 8, 10, 12, 14, 16, 18, 20, 24, 30 and 36 K. c, Dual-gate map of Rxx of Device 1 at TL = 35 mK. Correlated states for each side of the junction appear at integer values of ν1 and ν2. d, VPTE response in the electron-doped flat bands of Device 1 at TL = 10 K. Oscillations emerge around each integer filling. e, VPTE response near the CNP shows a characteristic six-fold symmetry, which confirms the thermoelectric origin of the response. Dashed lines in d and e are visual guides. Insets: linecuts of the dual gate map along the horizontal and vertical dashed lines, where one of the top gates is kept at neutrality. All gate voltage dependences are plotted as a function of the filling of the moiré bands. This conversion is calculated using the carrier density at full filling and the gate capacitances, which are both extracted from magneto-transport data.
The continuous-wave excitation induces a local increase in the electronic temperature ΔTe centred at the junction’s interface. Using the split top gates, we established a chemical potential difference Δμ (and so a Seebeck coefficient difference ΔS) across the junction. The gate-dependent response around the CNP exhibits multiple sign changes in a characteristic six-fold pattern (Fig. 1e), as reported previously for single-layer graphene38. This pattern reflects the antisymmetric gate-dependence of S in e–h-symmetric semimetals and semiconductors. Here, the sign of the net PTE voltage (VPTE) does not depend only on the polarity of the junction (p–n or n–p), as in the photovoltaic effect, but is instead determined by the Seebeck coefficient on each side of the junction (the sign of the response is reversed between pp+ and p+p). This clearly establishes the PTE effect as the origin of the optoelectronic response38,39. In the Supplementary Information we discuss and rule out contributions from other potential mechanisms of voltage generation.
We consistently found six-fold symmetric patterns around the CNP across multiple samples and various experimental conditions (Supplementary Fig. 18). This results in a net PTE voltage given by VPTE = −(S2 − S1)ΔTe, with Si(μi) the Seebeck coefficient of each side of the junction38,39,40,41 (see the lower left sketch in Fig. 1a). We note that the PTE effect confers multiple advantages for the study of thermoelectric transport, including spatial control of the ΔTe profile and efficient carrier heating in graphene-like systems42,43.
The PTE response indicates graphene-like, hot carrier dynamics in MATBG for above-gap excitation. Here the absorbed photon energy is efficiently converted into an increased temperature Te + ΔTe of the carrier distribution at EF, while the phonon degrees of freedom stay in equilibrium at lattice temperature TL (ref. 44). As the MATBG flat bands lie near EF, thermoelectric transport of the hot carriers serves as a powerful tool to probe the low-energy electronic spectrum of MATBG. This picture is consistent with existing studies of light–matter interactions in MATBG in this wavelength range45,46, which we discuss in Supplementary Section V. In the following, we leverage the PTE response of the p–n junction to investigate the low-energy electronic spectrum of the strongly interacting flat bands.
We explored the thermoelectric response of the p–n junction, focusing on the conduction flat band (ν > 0), which exhibits stronger correlated states in transport. In Fig. 1d, the dual gate map of VPTE(ν1,ν2) reveals multiple sign changes that appear at integer νi for each side of the junction. These features coincide with the correlated states in the dual-gate Rxx map, indicating that VPTE captures the interaction-driven instabilities of the MATBG flat bands11,12,13. To study these oscillations in more detail, we simplified the measurement scheme by fixing one side of the junction at the CNP, so that S2 = SCNP = 0. The PTE response then reads VPTE = −(S2 − S1)ΔTe = S1ΔTe, and can be directly linked to S1. We focused on this side of the junction because Rxx(ν1) exhibits larger resistive peaks than Rxx(ν2). This measurement scheme mimics the configuration used in Joule heating approaches, which feature a homogeneous S and an asymmetric ΔTe. We restricted ourselves to the linear heating regime (ΔTe Te = TL) by using low excitation powers. We estimated ΔTe using a steady-state, two-temperature model that includes the experimentally determined thermal relaxation time of the devices (Supplementary Section IV).
The low-temperature, gate-dependent thermoelectric response VPTE(ν1) of both devices is shown in Fig. 2a. The evolution of VPTE across the CNP is conventional, exhibiting an antisymmetric, sign-changing doping dependence, where holes result in a positive S and electrons in a negative S. Following electron doping of the flat bands, we observed oscillatory features of the thermoelectric response around each integer ν1. These oscillations can be attributed to the formation of symmetry-breaking ground states36. Strikingly, VPTE remains electron-like (negative) at ν1 = 1,2, despite the prominent gap-like oscillations. This sign-preserving thermoelectric response contrasts with the SMR expectation, where the Seebeck coefficient SMott should cross zero when the carrier type changes across gaps or at extrema of the density of states. The negative sign of VPTE indicates reduced hole contributions to thermoelectricity, highlighting the pronounced e–h asymmetry of the charge excitations of the symmetry-broken ground states.
Fig. 2: Sign-preserving thermoelectric responses in the flat bands at low temperatures.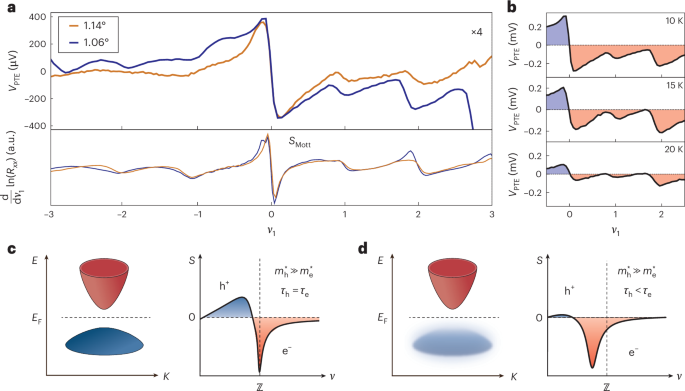
a, PTE response across the flat bands at TL = 10 K under low-power excitation for Device 1 (θ = 1.14°) and Device 2 (θ = 1.06°). In this measurement, S2 = 0. Bottom: expectation from the semiclassical Mott formula, where \({S}_{{\mathrm{Mott}}}\propto \frac{\text{d}}{\text{d}{\nu }_{1}}\mathrm{ln}({R}_{{xx}})\). The response of Device 1 has been scaled by a factor of 4. b, Temperature-dependent thermoelectric response for Device 2 at 10 K (top), 15 K (middle) and 20 K (bottom). As TL increases, the response evolves towards conventional sign-changing thermoelectricity at integer fillings. c, Left: two-band model for a generic symmetry-broken ground state at \(\nu\,{\mathbb{=}}\,{\mathbb{Z}}\) with large effective mass asymmetry (\({m}_{\mathrm{h}}^{* }\gg {m}_{\mathrm{e}}^{* }\)) and equal scattering lifetimes τh = τe. Right: computed Seebeck coefficient in the scenario of extreme mass asymmetry (\({m}_{\mathrm{h}}^{* }=150\,{m}_{\mathrm{e}}^{* }\)), exhibiting slight e–h asymmetry but preserving the sign change near \(\nu\,{\mathbb{=}}\,{\mathbb{Z}}\). d, Left: band structure for \(\nu\,{\mathbb{=}}\,{\mathbb{Z}}\) in a two-band, light–heavy scenario where the two bands feature distinct scattering rates (carrier lifetimes). The hole band has a shorter carrier lifetime, illustrated by spectral broadening of the states (τ ∝ 1/ΔE). Right: computed Seebeck coefficient in the light–heavy scenario with \({m}_{\mathrm{h}}^{* }=150\,{m}_{\mathrm{e}}^{* }\), τe = 6τh. The lifetime asymmetry drastically modifies the Seebeck coefficient, which becomes fully negative across the integer filling.
In the electron-doped flat bands (ν1 > 0), the magnitude of VPTE decreases for increasing TL, as shown in Fig. 2b. Within the studied temperature range, the Seebeck-driven response did not extrapolate to zero as TL → 0. This observation, previously reported in strongly correlated systems17,18,19,20,23, underscores the key role of non-semiclassical correlation effects in thermoelectric transport in the MATBG flat bands. The hole peak in the VPTE oscillations around ν1 = 1,2 recovers its positive sign at TL = 20 K, in agreement with the computed ordering temperatures of the symmetry-broken phases in MATBG47.
In Fig. 2c,d we illustrate different scenarios for e–h asymmetry in the electron-doped correlated states. Following the interaction-induced reconstruction of the Fermi surface, the MATBG flat bands are known to support symmetry-broken ground states at integer fillings \(\nu ={\mathbb{Z}}\). The charge-one excitations above these ground states can be phenomenologically modelled by two quadratically dispersing bands around EF (Fig. 2c)30,31. We first considered strong mass asymmetry of the bands as the potential origin of the sign-preserving thermoelectric response. In this scenario, the hole band has larger effective mass \({m}_{\mathrm{h}}^{* }\gg {m}_{\mathrm{e}}^{* }\), but all carriers share a common carrier lifetime τ. Within a two-band model36, we computed S under conditions of extreme mass asymmetry (\({m}_{\mathrm{h}}^{* }=150{m}_{\mathrm{e}}^{* }\)). The Seebeck coefficient (Fig. 2c, right) exhibits reduced hole-like contributions but still features a zero crossing across the gap. The persistence of the sign change suggests that asymmetry in the dispersion of the electron and hole bands is insufficient to explain the observed behaviour. Other factors beyond the band dispersion, such as the carrier scattering rate in the flat bands, must also be considered.
Realistic modelling of the transport properties of the correlated states of MATBG must account for the energy (or band) dependence of the carrier lifetime τ = τ(E). Next, we included a band-dependent carrier lifetime in the two-band model (Fig. 2d). By considering τe = 6τh and maintaining the mass asymmetry ratio at \({m}_{\mathrm{h}}^{* }=150{m}_{\mathrm{e}}^{* }\), we replicated the electron-like oscillations of the Seebeck coefficient (Fig. 2d). In this scenario, hole-like transport is suppressed through the combined effects of the increased scattering rate, which reduces τh, and the lower group velocity vg(E) of the hole band. Notably, S exhibits electron-like characteristics even for sizable hole doping of the symmetry-broken ground state at \(\nu ={\mathbb{Z}}-{\rm{\delta }}\). This observation strongly suggests that the energy dependence of τ(E), set by the scattering processes, profoundly influences the thermoelectric transport of such general correlated ground states. Similar effects have been reported in other strongly correlated systems23,24, including heavy fermion compounds21,48. In localized heavy bands, e–e interactions can induce large scattering rates that result in shorter transport lifetimes and diminished transport contributions.
While this minimal model already contains the main features needed to explain the anomalous PTE response—the mass and lifetime asymmetry—we further compared our results with the recently developed THF mapping of MATBG35. In the THF model, the flat bands result from the hybridization between strongly correlated, highly localized heavy f electrons and highly dispersive, itinerant light c electrons (Fig. 3a). The topology is then carried by the light electrons, while the flatness of the bands is a direct consequence of the localized nature of the heavy electrons. This model therefore naturally accommodates coexisting electronic species with contrasting transport coefficients. The c electrons form coherent excitations that dominate the transport properties, whereas the incoherent excitations formed by f electrons do not contribute directly to transport. Indirectly, however, the strong interactions between localized f electrons may impact electronic transport by breaking the global symmetries of MATBG and inducing gaps in the dispersion of the c electrons. In what follows, we provide a microscopic model for the low-temperature thermoelectricity of MATBG by considering the symmetry-broken phases of the THF model. The latter have been shown to persist for finite doping and relatively low temperatures47.
Fig. 3: Seebeck coefficient of the symmetry-broken ground states in the THF model.
a, Illustration of the coexisting electronic species in the THF mapping of MATBG. The c electrons (red) are itinerant and weakly interacting, while the f electrons (blue) are highly localized in the moiré scale and incoherent due to strong electronic interactions. b–d, THF band structures for the KIVC symmetry-broken correlated ground states around ν = 0 (b), 0.8 (c) and 2 (d). The colour coding of the bands indicates their light or heavy character. The band structure in c is shown away from ν = 1 to highlight the spectrally broadened f states. e, Seebeck coefficient for the KIVC state in b at ν = 0. f, Seebeck coefficient for the KIVC + valley-polarized (VP) state in c in the vicinity of v = 1. g, Seebeck coefficient for the KIVC state in d in the vicinity of v = 2. At positive, non-zero integer fillings, the hole bands are formed by incoherent f electron excitations and give rise to a sign-preserving, oscillating Seebeck coefficient. The Seebeck coefficients in e–g are computed for T ≈ 0.65Torder.
Using self-consistent second-order perturbation theory36, we computed the interacting energy bands and corresponding Seebeck coefficients for the correlated insulating ground states of MATBG at twist angle θ = 1.06°. All computed band structures and S correspond to temperatures T ≈ 0.6–0.7Torder, where Torder denotes the self-consistently determined ordering temperature of each ground state. The low-temperature band structures of the Kramers intervalley coherent (KIVC)35,49, or KIVC + valley-polarized, ground states near integer fillings ν = 0,1,2 are shown in Fig. 3b–d. The colour coding denotes the light (c) or heavy (f) character of the bands (Fig. 3a). The coherent (incoherent) excitations appear as sharp (blurred) energy states, associated with long (short) transport lifetimes. Generally, the c electron states form the bands near Γ, while f states appear away from the Brillouin zone centre.
The essential properties of the THF band structures discussed here do not depend on the exact choice of the symmetry-broken ground state36. Other states, such as the intervalley coherent Kekulé spiral state50, can be considered but do not change the light–heavy dichotomy in the dispersion of the symmetry-broken states. At ν = 0, the bands near EF consist of light excitations for both holes and electrons. As the charge ±1 excitations are symmetric around EF, the Seebeck coefficient (Fig. 3e) exhibits a conventional antisymmetric line shape, consistent with our observations for MATBG near CNP (Fig. 1e).
The interacting THF band structures for the symmetry-broken ground states at non-zero integer ν (shown in Fig. 3c,d) exhibit a marked asymmetry of the charge ±1 excitations. We found that the low-energy hole-like excitations correspond to localized f states, while itinerant c electrons form the bands just above EF. The strong interactions between f states lead to a reduced τ for the heavy carriers near EF. Indeed, we found that the symmetry-broken correlated insulators at positive integer fillings replicate the light–heavy scenario sketched in Fig. 2d, as the weakly dispersive hole band features states with reduced carrier lifetimes.
We then computed the Seebeck coefficient for the symmetry-broken states at non-zero integer fillings (Fig. 3c,d). The hole-like contributions to thermoelectricity are quenched due to the reduction of τ for the localized f states, resulting in a fully negative Seebeck coefficient across the interaction-driven gaps near ν = 1,2. These findings align well with our experimental observations (Fig. 2a). Notably, for ν = 1,2, the negative peak of S is shifted towards the CNP in the theoretical computations. This effect, also present in the experimental data, arises from the highly broadened spectral weight of the f-electron bands below EF (ref. 33). Detailed THF band structures and Seebeck coefficients for different ground states, fillings and temperatures are presented in ref. 36.
Overall, the light–heavy structure of the symmetry-broken correlated states within the THF model provides a natural explanation for the observed PTE response at low temperatures. The crucial role of the finite carrier lifetimes of the f states is emphasized in the observation of a negative, sign-preserving Seebeck coefficient. From the measured response and the estimated ΔTe (Supplementary Section IV), we obtained S ≈ 50–150 μV K−1 for TL = 10 K across the conduction flat band, in good agreement with theoretical computations36 and previous reports26,27,28. We note that, while the Seebeck coefficient is typically small in semimetals, due to e–h compensation, the asymmetry in dispersion and lifetime in the correlated states of MATBG leads to a large Seebeck coefficient.
We now focus on thermoelectric transport at higher lattice temperatures. As the temperature rises, the symmetry-broken ground states disappear and MATBG transitions into a symmetry-preserving unordered state47,51, with Hubbard bands observed in scanning tunnelling microscopy experiments52,53. Theoretical calculations estimate the critical temperature for this symmetric state to be around 10–20 K (ref. 47). The PTE response at TL = 30 K and 50 K for an absorbed optical power Pabs = 5.47 μW is illustrated in Fig. 4a. Unlike the low-temperature behaviour, we observe hole-like thermoelectricity with S > 0 for 0 ν1 4a). However, the distinct gap-like oscillations around each integer ν1 (Fig. 4b) indicate the persistence of electron correlations in the high-temperature, symmetric state.
Fig. 4: Thermoelectric response in the high-temperature, symmetric state of MATBG.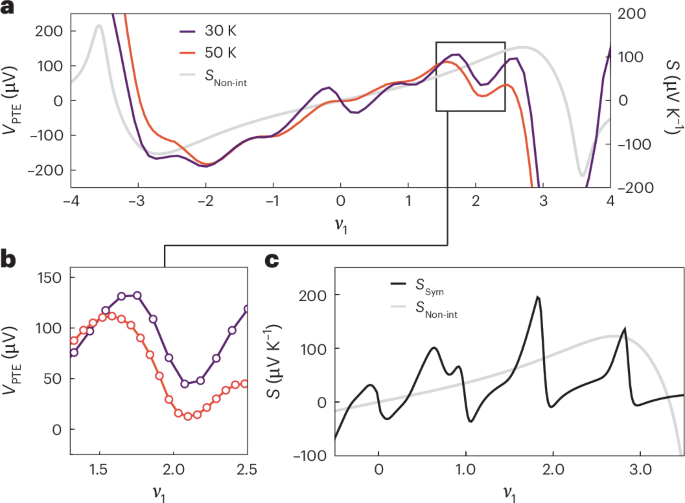
a, PTE response in Device 2 (θ = 1.06°) at TL = 30 K (purple) and 50 K (red). The grey trace shows the expectation from the non-interacting limit of the THF model (SNon-int) for TL = 15 K, τe/τh = 4. b, Zoom-in of the high-temperature oscillations of the thermoelectric response near ν = 2. c, SSym of the THF model at TL = 15 K. The grey trace depicts SNon-int at the same temperature.
To model the high-temperature thermoelectric transport, we used the THF model with identical parameters to the low-temperature case. However, we examined symmetric solutions, in which none of the model’s symmetries are spontaneously broken36,51,54. The computed symmetric Seebeck coefficient SSym is illustrated in Fig. 4c for TL = 15 K, and shows marked oscillations at integer ν along with a positive (hole-like) offset, similar to the non-interacting scenario36. The oscillations arise from gap openings through interactions between the localized f states. Overall, the THF model qualitatively reproduces the Seebeck effect at high temperatures under the assumption that the solution must preserve symmetry. The temperature mismatch between the theory and experiment stems from less precise modelling of the non-interacting dispersion, which is susceptible to extrinsic effects such as strain or lattice relaxation.
The PTE response at elevated temperatures highlights the presence of electron correlations beyond the ordering temperatures of the symmetry-broken ground states. The qualitative match with the Seebeck coefficient for the symmetric solution of the THF model provides further support for heavy fermion physics in MATBG. These findings also emphasize that electron interactions can induce gap openings in the electronic spectrum of the flat band even when all system symmetries are preserved.
While the band asymmetry of the correlated ground states has been predicted in other theoretical frameworks29,30,31,32,33, heavy fermion mapping of MATBG35 offers two distinct advantages. First, it enables computations beyond the Hartree–Fock level, allowing us to self-consistently obtain the band and state-resolved carrier lifetime, which is central to the observed low-temperature behaviour. Second, it provides an intuitive picture of the contrasting ground states observed in the MATBG flat bands based on the coexistence of distinct carrier types with different masses and scattering rates.
Future studies of the thermoelectricity of MATBG flat bands could investigate the Nernst effect21,55 or locally map thermoelectric transport56. The role of phonon drag contributions, particularly for Joule heating schemes, remains an open question due to the limited experimental insight into the phonon spectrum of MATBG and its coupling to electronic transport57,58. The signatures of coexisting light and heavy electrons reported here also motivate the investigation of Kondo physics in van der Waals heterostructures59,60,61,62.
In terms of applications, the large measured PTE response (and predicted Seebeck coefficient) suggest the potential for applications of MATBG as a thermoelectric material; for example, in active thermoelectric cooling at cryogenic temperatures55,63. Correlated materials have been proposed before as excellent candidates for thermoelectric materials22,64. Future MATBG devices based on the PTE effect could leverage broadband absorption65, efficient carrier heating42,43 and ultrafast thermal relaxation57.