Synthesis
Ternary Au56In28.5Eu15.5 and Au54In27.5Sn3Eu15.5 iQC alloys were synthesized using the arc-melting technique. High-purity raw elements of Au (99.99 wt%), In (99.99 wt%) and Eu (99.9 wt%) were utilized in the synthesis process. During the arc-melting process, a relatively low current of 70 A is applied to melt the raw materials and to prevent the vapourization of Eu. The samples are flipped and remelted three times to ensure compositional homogenization. At the final stage of melting, to prevent the precipitation of second phases during cooling, the melt is rapidly cooled by immediately reducing the current from 70 A to 0 A.
Characterization
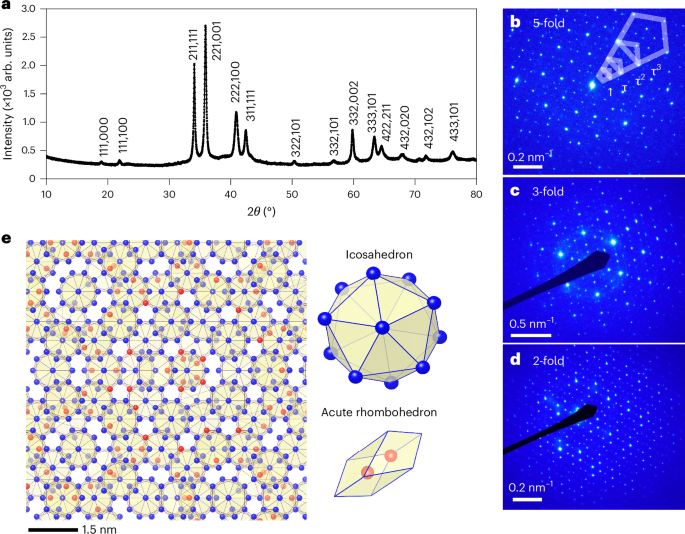
Phase identification was performed through powder XRD analysis using a Rigaku SmartLab SE X-ray diffractometer with Cu Kα radiation. To index the powder XRD pattern and estimate the 6D lattice parameter (a6D), Elser’s method was used. The reported a6D value in this study is an average of the estimates derived from the 211111, 221001 and 332002 peaks.
For phase characterization, selected-area electron diffraction patterns were acquired using the JEM-2010F transmission electron microscope located at the Advanced Research Infrastructure for Materials and Nanotechnology, the University of Tokyo. To prepare the sample for selected-area electron diffraction analysis, the bulk material was initially crushed in ethanol, and the resulting small particles were then transferred onto a copper grid.
For microstructural characterization, scanning electron microscopy (JEOL JSM-IT100) was utilized.
Magnetization measurements
Bulk magnetization measurements were performed using a superconducting quantum interference device magnetometer, Quantum Design MPMS3. These measurements were carried out over a temperature range spanning from 0.4 K to 300 K, with an external d.c. field up to 7 × 104 Oe. Both ZFC and FC conditions were examined during these measurements.
Neutron diffraction
Neutron powder diffraction experiments were performed using the high-resolution powder diffractometer ECHIDNA installed at the OPAL reactor, Australian Nuclear Science and Technology Organization. Because of the high neutron absorption of all the constituent elements, namely, Au, In and Eu, neutrons with a relatively short wavelength (λ = 1.6220 Å) were selected using Ge 335 reflections. In addition, the powder sample was loaded in the double-walled vanadium can with inner and outer radii of 4.74 mm and 5.29 mm, respectively, to reduce the attenuation effect. The can was set in a closed-cycle 4He refrigerator with a base temperature of 3 K. A complementary neutron diffraction experiment was performed using the thermal-neutron triple-axis spectrometer ISSP-GPTAS installed at JRR-3. Incident neutrons with ki = 3.83 Å−1 (λ = 1.64 Å) were selected using pyrolytic graphite 002 reflections, and higher-order harmonic neutrons were removed using two pyrolytic graphite filters. To reduce the background, a triple-axis setup with a pyrolytic graphite 002 analyser was used, and 40′-40′-40′-80′ collimations were used. The finely pulverized sample was pasted on a single-crystal Si plate using CYTOP as a glue. The thickness of the Si plate was 0.5 mm, whereas the dimensions of the pasted pulverized sample were 38 mm (w) × 38 mm (h) × 0.4 mm (t). The sample-pasted plate was sealed in the Al sample can with the 4He exchange gas to achieve thermal homogeneity. The sample can was set to the closed-cycle 4He refrigerator with the Si plate bisecting the angle between –ki and kf, that is, the transmission geometry. The base temperature of the triple-axis experiment is approximately 3 K.
Neutron powder diffraction analysis
The neutron powder diffraction patterns of Au56In28.5Eu15.5 iQC were analysed using the custom-built Rietveld and Pawley analysis code msas6D, which is capable of refining the atomic structure of the QC using 6D crystallography (T.J.S., manuscript in preparation). The peak profile function used in the following analysis is the split pseudo-Voigt function39, and the profile parameters estimated using a standard alloy sample were used as the fixed parameters.
For the atomic structure analysis, the published crystal structure of Cd–Yb iQC32 was further simplified as follows. The shapes of the occupation domains (ODs) for all the atoms are approximated to be spherical (or spherical shell) instead of polyhedral40. The positions of the ODs in the 6D chemical unit cell are (0, 0, 0, 0, 0, 0) (V site), (1/2, 0, 0, 0, 0, 0) (E site), (1/2, 1/2, 1/2, 1/2, 1/2, 1/2) (B site) and (0, 1/4, 1/4, 1/4, 1/4, 1/4) (rare-earth site). Note that the rare-earth OD is not centred at the B site as assumed in the earlier refinement using the polyhedral ODs. This is because the polyhedral ODs at the B site assumed in the earlier refinement consist of several small ODs corresponding to different atoms. Indeed, the small ODs for the rare-earth atoms may be approximated by spherical ODs centred at (0, 1/4, 1/4, 1/4, 1/4, 1/4). For the analysis of the Au–In–Eu iQC, the rare-earth site is assumed to be fully occupied by Eu atoms, whereas other ODs are assumed to be randomly occupied by Au and In atoms with the ratio 56:28.5. Since the purpose of atomic structure refinement is just to obtain a reasonable nuclear reflection pattern that can be used to discriminate magnetic reflections and not to obtain the final atomic structure, we refine the outer radii of the ODs only with fixed occupancy (the OD of the B site is a spherical shell with the inner radius fixed to 7.95 Å, whereas all the other ODs are spherical). The resulting radii of the ODs are 6.2(2) Å, 6.58(6) Å, 8.4(1) Å and 4.00(4) Å for the V, E, B and rare-earth sites, respectively. Nonetheless, we do not claim that these values represent the correct 6D atomic structure due to the oversimplifications in the present modelling. The lattice parameter (Penrose edge length) a is refined as 5.5351(4) Å at T = 10 K, which gives the 6D lattice constant a6D = 7.8277 Å.
The magnetic reflections were fitted assuming that the magnetic unit cell in six dimensions is doubled compared with the chemical unit cell. Accordingly, the lattice parameter for the 6D magnetic unit cell is fixed to 2a6D = 15.656 Å (that is, the magnetic unit cell size 2a6D × 2a6D × 2a6D × 2a6D × 2a6D × 2a6D) in the magnetic peak refinement. Due to the lack of any magnetic structure model in the 6D space at present, we use the Pawley method41 to fit the magnetic diffraction pattern with all the integer indices with the perpendicular space component |Q⊥| −1. Only the reflections up to 2θ = 40° are included in the magnetic fitting, as the magnetic intensity decreases rapidly at high 2θ.
The result of the combined Rietveld (nuclear) and Pawley (magnetic) fittings is shown in Supplementary Fig. 6a. Nuclear reflections appearing at around 2θ ≈ 35° are well fitted, indicating that the peak widths are resolution limited with the present instrumental resolution. The magnetic peaks (indicated by the arrows) are also well reproduced by the fitting. To observe the magnetic scattering part much closely, we performed Pawley fitting to the temperature-subtracted magnetic diffraction pattern. Figure 3b shows the result of the magnetic Pawley fitting with the doubled magnetic unit cell and |Q⊥| −1. Magnetic reflections are well indexed with indices that include at least one odd number, clearly confirming the antiferromagnetic nature of the magnetic reflections. Note that each magnetic peak is not from a single reflection, but possibly results from the overlap of two reflections, making it difficult to uniquely determine the magnetic modulation vector.
To further confirm the antiferromagnetic nature of the observed magnetic peaks, we performed the following two analyses. First, the temperature-subtracted magnetic diffraction pattern is Pawley fitted using larger |Q⊥| −1. It should be noted that this |Q⊥| range includes all nuclear reflections, such as 111000 (222000 in a doubled magnetic unit cell), as candidate magnetic reflections. The result of the fitting is shown in Supplementary Fig. 6b, which clearly indicates that all-even indices do not give substantial intensity contribution to the observed magnetic diffraction pattern, confirming the antiferromagnetic nature. Second, the T = 3 K diffraction pattern was fitted with the combined Rietveld and Pawley method, assuming integer indices of the original chemical unit cell for the magnetic reflections, the result of which is shown in Supplementary Fig. 6c. Clearly, the integer indices of the original chemical unit cell cannot reproduce the magnetic peak positions, conclusively excluding the ferromagnetic nature in this Au–In–Eu iQC.