Topological phonons
Like topological electronic quasiparticles, topological phonons are characterized by topological invariants that are intimately related to crystalline symmetries. For instance, topological nodal-line phonons, which are characterized by the geometrical Berry phase, can emerge when crystals preserve mirror (R)/inversion (P) symmetry1. Weyl phonons, on the other hand, emerges in non-centrosymmetric structures and are described by the Chern number (C)2,3. As an example, we consider the following effective two-orbital Hamiltonian:
$$H\left({{\boldsymbol{q}}}\right)=\left(\begin{array}{cc}A{q}_{x}{q}_{y}{q}_{z} & {B}^{*}({q}_{x}^{2}{+\omega }^{2}{q}_{y}^{2}+\omega {q}_{z}^{2})\\ B({q}_{x}^{2}{+\omega }^{2}{q}_{z}^{2}+\omega {q}_{y}^{2}) & -A{q}_{x}{q}_{y}{q}_{z}\end{array}\right)$$
(1)
where \(\omega={e}^{\frac{2\pi i}{3}}\), A is a real constant and B is a complex constant. The qx/y/z are pseudo-momentum of phonons. This Hamiltonian is defined as a square root of the dynamical matrix, with its eigenvalues \({\psi }_{\pm }\) being the phonon polarization vector, \({\varepsilon }_{q,\pm }\), and its eigenvalues being the frequencies of the phonons. Equation (1) describes the lattice dynamics in the vicinity of a twofold degenerate high symmetry point that respects chiral cubic symmetries and time-reversal symmetry (see Fig. 1). The topological number \(C=\pm 4\) can then be derived from the eigen vectors, \({\psi }_{\pm }\), of Eq. (1) and represent twofold quadruple Weyl phonons3,4.
Chiral phonons
Chiral phonons, also referred to as circularly polarized phonons, initially mean phonons with nonzero AM5,6, \({l}_{q,\sigma }\):
$${l}_{q,\sigma }=({\varepsilon }_{q,\sigma }^{{\dagger} }M{\varepsilon }_{q,\sigma }){{\hslash }}$$
(2)
where \({{{\boldsymbol{\varepsilon }}}}_{{{\boldsymbol{q}}},\sigma }\) is the polarization vector for phonon mode σ at momentum q, \(({M}_{i})_{{jk}}=(-i){\varepsilon }_{{ijk}}\bigotimes {I}_{n\times n}\) (i,j,k = x,y,z) is a product of the generator of SO(3) rotation and the unit matrix for a unit cell with n atoms, and \({\varepsilon }_{{ijk}}\) is the Levi-Civita symbol. From a symmetry point of view, chiral phonons with finite AM are widely present in crystals, unless certain symmetries restrict the AM to be zero, such as mirror, spatial inversion, or time-reversal symmetry.
Phonon modes with \({\widehat{C}}_{n}\)-symmetry
Although AM is a fundamentally important concept with significant macroscopic consequences, it is usually not conserved in microscopic quasiparticle scattering processes. Instead, the pseudo-angular momentum (PAM), \({l}_{q}^{{ph}}\), has been introduced in systems with rotational or screw rotational symmetries7,8,9,10,11:
$${\widehat{C}}_{n}{{{\boldsymbol{u}}}}_{q}={e}^{-\frac{2\pi i}{n}\cdot {l}_{q}^{{ph}}}{{{\boldsymbol{u}}}}_{q}$$
(3)
$${{{\boldsymbol{u}}}}_{q}={{{\boldsymbol{\varepsilon }}}}_{q}{e}^{i({{{\boldsymbol{R}}}}_{l}\cdot {{\boldsymbol{q}}}-\omega t)}$$
(4)
where \({\widehat{C}}_{n}\) is the rotation or screw rotation operator and \({{{\boldsymbol{u}}}}_{q}\) is the phonon Bloch wave function at q. Since \({l}_{{{\boldsymbol{q}}}}^{{ph}}\) originates from phase factors acquired by discrete \({\widehat{C}}_{n}\) symmetry, the phonon PAM can only be defined at rotation-invariant momenta, and it is conserved modulo n.
Connections between topological and chiral phonons
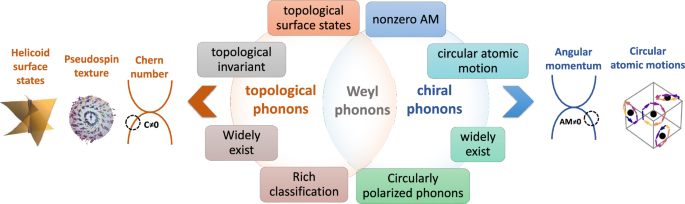
Topological and Weyl phonons are prevalent in materials, particularly in chiral crystals. Symmetries of the system constrain phonon modes, thereby determining topological and chiral properties. Here we use Weyl phonons to draw the connection between these independently developed fields. Consider Eq. (1) as an example, the eigen vector \({\psi }_{\pm }\) can be analytically derived in the twofold quadruple Weyl system BaPtGe that features chiral lattice motions3,4, as shown in Fig. 1. Indeed, this connection is general for non-centrosymmetric materials, where topological phonons are Weyl phonons with nonzero AM. Namely, Weyl phonons are characterized by the Chern number, which is an integral of the Berry curvature. Since the Berry curvature has the same symmetry with the phonon AM, the nonzero Chern number implies that the phonon AM should be nonzero around the Weyl point. Therefore, Weyl phonons are a special type of chiral phonons, as highlighted in Fig. 1. Since phonons can be chiral even away from point or line degeneracies, chiral phonons are not necessarily topological.
Furthermore, it has been shown that3 Weyl phonons can be classified based on the (screw) rotational symmetries \({\widehat{C}}_{n={\mathrm{3,4,6}}}\), which also determines the phonon PAM (see Eq. (3)). Therefore, the Chern numbers C of Weyl phonons can be derived from the PAM of the degenerated phonon modes12,13. This mapping is, however, symmetry-dependent.
Experimental evidence of topological phonons and chiral phonons
Topological phonons were first revealed using inelastic X-ray scattering (IXS)14. By quantitatively comparing the IXS-determined phonon dynamical structure factor, \(S\left({{\boldsymbol{Q}}},\omega \right)\), and density functional theory calculated \(S\left({{\boldsymbol{Q}}},\omega \right)\), the double Weyl phonons, hence chiral phonons as described in the previous section, are established in the P-breaking crystal FeSi14. Observations of truly chiral phonons were also reported in Raman and resonant inelastic x-ray scatterings7,8,14,15. The topologically trivial chiral phonons in 2D transition metal dichalcogenides WSe2 were first reported by using the circular dichroism (CD) in the transient infrared spectroscopy16.