Quantum computers promise revolutionary computational power, but maintaining the delicate quantum states of qubits remains a significant hurdle, with errors constantly threatening calculations. Kathleen Chang, Qile Su, and Shruti Puri, all from Yale University, and their colleagues demonstrate a novel approach to tackling a particularly troublesome type of error known as coherent noise, which is notoriously difficult to manage. Their research reveals that teleportation, a quantum communication technique, effectively transforms these complex coherent errors into simpler Pauli errors, for which robust correction methods already exist. This breakthrough is significant because it allows researchers to accurately predict and improve the performance of quantum error correction codes, potentially paving the way for more stable and reliable quantum computers and removing the need for complex error mitigation strategies.
Surface Code Error Analysis and Bounds
This document presents a rigorous theoretical framework for understanding how to protect quantum information from errors using a technique called surface code error correction. It focuses on analyzing how errors spread and accumulate within the code, aiming to prove that errors can be suppressed to an arbitrarily low rate. The core idea is to track the size of errors, the number of affected qubits, as they propagate through the code, ensuring they remain manageable. The analysis employs mathematical tools like the union bound to estimate the probability of errors and determine the maximum error rate the code can tolerate.
The document begins by establishing a precise mathematical language for describing quantum errors and the surface code itself. It defines key concepts such as Pauli operators, error weight, and the distance of the code, a measure of its ability to correct errors. It then delves into the mechanics of error propagation, explaining how errors spread through the code due to measurements and interactions between qubits. The analysis considers the specific structure of the cluster state, a type of quantum state often used as the basis for surface codes, and extends to realistic noise models that include both bit flips and phase flips.
Ultimately, this work provides a foundation for proving the existence of an error threshold, a crucial step towards building reliable quantum computers. The significance of this research lies in its rigorous mathematical approach to error analysis and its potential to guide the design and implementation of quantum computers. By identifying the types of errors that are most critical to suppress, it helps researchers focus their efforts on building more robust and reliable quantum systems.
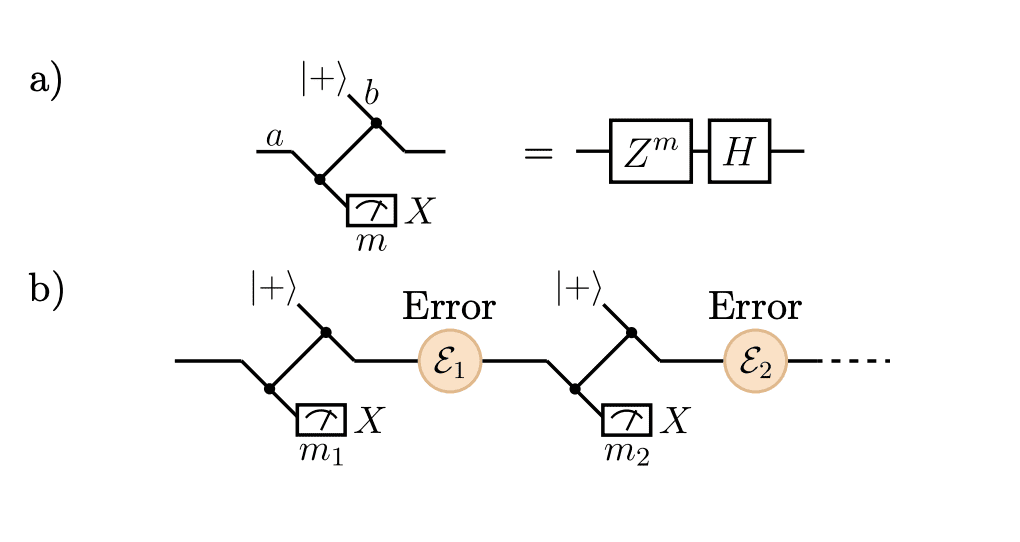
Teleportation Converts Coherent to Pauli Errors
Researchers have addressed a significant challenge in quantum error correction, the difficulty of dealing with coherent errors. Unlike the more commonly studied Pauli errors, coherent errors grow in a complex way that makes them difficult to simulate and correct. The team hypothesized that teleportation, a process for transferring quantum information, could transform these complex errors into the more manageable Pauli errors. By repeatedly teleporting quantum information, they demonstrated that the resulting errors behave in a predictable way. Specifically, they showed that repeated teleportation effectively “decoheres” the coherent errors, reducing their complex behaviour and causing the overall error rate to grow at a manageable pace, similar to that of Pauli errors.
A key innovation was the development of a model demonstrating that teleported quantum codes behave equivalently to standard Pauli error models under specific conditions. By considering realistic scenarios where small rotations accompany each quantum gate operation, the team proved that the resulting error behaviour is equivalent to a Pauli error model. This allows researchers to utilize existing tools and techniques developed for Pauli error correction and efficiently simulate the performance of these codes on classical computers. This approach circumvents the need for complex simulations required to analyze coherent errors directly and provides a pathway to analytically prove the existence of a threshold for reliable quantum computation. The ability to accurately predict and control error rates is crucial for building practical quantum computers, and this work suggests that teleportation-based error correction could offer a robust and efficient solution. The inherent noise-tailoring property of teleportation may even eliminate the need for randomized compiling, a technique often used to improve the performance of quantum algorithms.
Teleportation Converts Coherent Errors to Correctable Noise
Researchers have demonstrated a significant advance in the quest for reliable quantum computers by tackling the challenge of coherent errors, a particularly insidious form of noise that hinders quantum calculations. Unlike more commonly studied incoherent errors, coherent errors arise from precise, predictable disturbances and can accumulate constructively, potentially overwhelming error correction strategies. This work establishes that the process of teleportation, a key technique for transferring quantum information, intrinsically transforms these problematic coherent errors into Pauli errors, a type of noise that is far better understood and easier to correct. The team first showed that repeatedly teleporting a single qubit effectively diminishes coherent errors, behaving similarly to how Pauli errors accumulate, a crucial finding as it suggests a pathway to control coherent noise.
Further analysis revealed that under a realistic model of coherent errors, specifically, small rotations occurring throughout a quantum calculation, teleportation simplifies the error landscape. Remarkably, the researchers proved that this teleportation-induced simplification renders the overall error model equivalent to one based solely on Pauli errors. This equivalence is profoundly important because it means that existing methods for analyzing and correcting Pauli errors can now be applied to scenarios involving these previously intractable coherent errors. Consequently, the performance of quantum error correction codes implemented using teleportation or measurement-based approaches can be accurately simulated using conventional computers, and, critically, an analytically provable threshold for reliable operation can be established. This breakthrough potentially removes the need for complex techniques like randomized compiling, which are currently used to convert coherent errors into Pauli errors, streamlining the path towards fault-tolerant quantum computing.
Teleportation Converts Coherent Errors to Pauli Errors
The research demonstrates that coherent errors, a significant challenge in quantum computing, can be effectively transformed into Pauli errors through the process of teleportation. This is achieved because teleportation effectively decoheres the initial coherent errors, resulting in an error rate that grows linearly with the number of teleportation steps, comparable to the behaviour of Pauli errors. Importantly, the team showed that coherent errors affecting both code and ancilla qubits become equivalent to Pauli errors when using teleportation-based error correction schemes. This finding is significant because Pauli errors are well understood and can be efficiently simulated on classical computers, allowing for accurate analysis of quantum error correction performance and the establishment of provable code thresholds. The ability to map coherent errors onto Pauli errors removes a major obstacle in simulating and optimising quantum computations, potentially eliminating the need for computationally expensive techniques like randomized compiling.