Transition-metal dichalcogenides (TMDs) are direct-gap semiconductors that can host optically bright excitons corresponding to Coulomb-bound electron–hole pairs. Due to the two-dimensional nature of TMDs, along with the large effective masses of electrons and holes and small dielectric permittivity of the surrounding medium, excitons are tightly confined, with the Bohr radius substantially smaller than the typical separation between doped charges1. These features make excitons in TMDs a promising tool for optical probing of many-body electron correlations. In particular, understanding the exciton fine structure of a doped sample has proven pivotal for a number of recent discoveries. Examples range from investigating polaronic dressing effects, which manifest through exciton line splitting into attractive and repulsive branches2, to probing correlated many-body phases using excited-state spectroscopy3, to observing electron crystalline states via umklapp scattering4 and to studying the rich magnetic properties of TMDs5,6,7. While most prior studies have focused on intralayer excitons, where both the exciton electron and hole reside in the same TMD layer, bilayer TMDs can host interlayer excitons (Fig. 1a,b), where the electron and hole are separated across the two layers8. However, interlayer excitons typically have weak optical transition dipole moments, posing challenges for optical measurements. In materials like MoS2 homobilayers, intra- and interlayer excitons strongly hybridize9,10,11, making interlayer excitons optically bright and enabling their use for optical probing of electronic correlations.
Fig. 1: The d.c. Stark effect of interlayer excitons.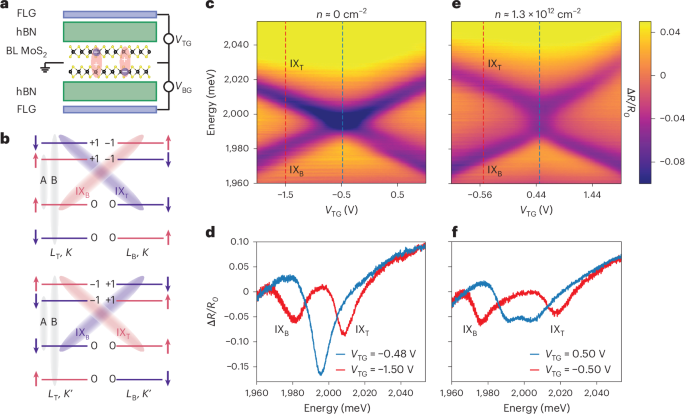
a, A schematic of a dual-gated 2H-stacked MoS2 homobilayer (BL MoS2) encapsulated with hBN. Tuning of the top and bottom gates, composed of a few layers of graphene (FLG), allows independent control of the total electron density n and out-of-plane electric field Ez. Interlayer excitons (IXs), highly sensitive to Ez owing to their large dipole moments, are also depicted. b, A schematic of the electronic band structure near the K valleys (top) and \({K}^{{\prime} }\) valleys (bottom) showing the relevant excitonic levels, electron spin and corresponding AQNs of the electronic bands, which determine optical selection rules. Top and bottom layers are labelled as LT and LB, respectively. c, In the undoped case n = 0, the energies of interlayer excitons shift linearly with Ez (VBG = −1.15VTG − 1 V), as can be seen in the simple crossing of exciton branches in the measured reflectance map ΔR/R0 at T = 8 K. d, The system exhibits two well-separated branches at a finite Ez ≠ 0, becoming degenerate at Ez = 0, with doubled oscillator strength. e, The d.c. Stark effect for the doped sample with n ≈ 1.3 × 1012 cm−2 (VBG = −1.15VTG + 1.25 V), showing that the simple crossing in c turns into a stochastic avoided crossing (Fig. 2). f, The linecut at VTG = 0.50 V, corresponding to Ez = 0, displays a broad feature with reduced relative amplitude compared with the undoped case in d.
Here, we experimentally investigate the properties of indirect excitons in a naturally grown 2H-stacked MoS2 homobilayer, integrated into a dual-gate device structure (Fig. 1a) whereby the top and bottom gate voltages, VTG and VBG, are simultaneously used to independently control the out-of-plane electric field Ez and the electron density n in the sample (Methods). The interlayer excitons have large permanent electric dipole moments ± dz (Fig. 1a), which make them highly sensitive to Ez. This can be studied by measuring reflectance contrast spectra (R − R0)/R0 = ΔR/R0 using a weak (optical nonlinearities are not relevant), incoherent white light source, where R is the reflectance obtained on the bilayer MoS2 flake and R0 is the reference spectrum at a high doping level (Methods). Figure 1c shows the undoped case (n = 0), illustrating the d.c. Stark effect, where the two interlayer excitons with opposite dipoles shift linearly with Ez and cross at Ez = 0 (VTG ≈ −0.48 V). The degeneracy point Ez = 0 is characterized by the amplitude doubling in the reflectance contrast spectrum of interlayer excitons, Fig. 1d (blue curve). When the sample is doped (n ≈ 1.3 × 1012 cm−2), as extracted from simulations based on a simple capacitance model in Supplementary Section I, the simple crossing in Fig. 1c turns into the elongated shape shown in Fig. 1e. This effect is highly reproducible across different collection light spots within the same sample, as well as in other similar devices (Supplementary Section II). The putative degeneracy point Ez = 0 (VTG ≈ 0.50 V), no longer exhibits the amplitude doubling (Fig. 1f). Instead, we observe a broadened feature with the overall amplitude roughly the same as that of individual interlayer excitons.
To understand these observations, we consider a simple model of two coupled harmonic oscillators describing the excitonic polarization response to the probe a.c. electric field \({\mathcal{E}}(t)\):
$$i\hslash {\partial }_{t}{X}_{{\rm{T}}}={\omega }_{{\rm{T}}}{X}_{{\rm{T}}}-i{\gamma }_{{\rm{T}}}{X}_{{\rm{T}}}+{\mathcal{W}}{X}_{{\rm{B}}}-{d}_{{\rm{T}}}{\mathcal{E}}(t),$$
(1)
and a similar equation holds for XB. Here, the variable XT/B represents the polarization oscillations associated with the interlayer exciton IXT/B (Fig. 1b), with the subscript referring to the layer of the electron; ωT/B = ±dzEz is the energy relative to the degeneracy point Ez = 0; γT/B is the total respective exciton decay rate; dT/B refers to the corresponding transition dipole moment; and \({\mathcal{W}}\) is the coupling strength between the two interlayer excitons, which we introduced for reasons that will become clear shortly. Physically, this coupling can be viewed as a permanent dipole flip-flop process.
Figure 2a depicts a simulated absorption map \({\rm{Im}\;}[\,\chi(\omega)]\), where χ(ω) is the polarization response function of the sample (Supplementary Section VII). This simulation corresponds to a simple crossing with \({\mathcal{W}}=0\) and closely resembles the measured signal for n = 0 in Fig. 1c. For \({\mathcal{W}}\ne 0\), an avoided crossing occurs, characterized by an asymmetry in intensities between the upper and lower exciton branches (Fig. 2b). This effect is attributed to constructive and destructive interference in the photon emission process of the corresponding exciton branches (Supplementary Section VIII).
Fig. 2: Stochastic interlayer exciton hybridization.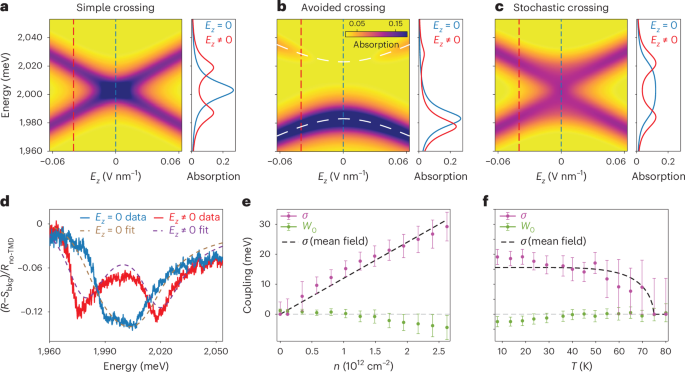
a–c, The simulated absorption map exhibits a simple crossing (a) as in Fig. 1c when the two excitons are uncoupled (\({{\mathcal{W}}}_{0}=0,\,\sigma =0\) in equation (2)), an avoided crossing (b) with asymmetry in the intensities of the two branches when the excitons are hybridized (\({{\mathcal{W}}}_{0}=-20\,\,\text{meV}\,,\,\sigma =0\)) and a stochastic crossing (c) reminiscent of Fig. 1e when the exciton coupling has a static, random character (\({{\mathcal{W}}}_{0}=0,\,\sigma =20\,\text{meV}\)). d, The measured reflectance contrast spectra are analysed using a few-parameter fit based on the model of stochastic coupling in equation (2); shown are two linecuts at n ≈ 1.2 × 1012 cm−2 corresponding to zero (blue curve) and non-zero electric fields (red curve), respectively. Such a fit (dashed lines) quantitatively captures both the linear Stark effect and the stochasticity of the interlayer exciton hybridization. Here, Sbkg is the fitted reflectance encoding background effects, while Rno-TMD is the measured reflectance at an optical spot away from the bilayer (Supplementary Section IX). e,f, The evolution of \({{\mathcal{W}}}_{0}\) and σ with the electron density n at T ≈ 8 K (e) and temperature T at n ≈ 1.3 × 1012 cm−2 (f). We find that both \(| {{\mathcal{W}}}_{0}|\) and σ increase (decrease) with increasing n (T), indicating a stronger hybridization between excitons at higher electron densities and lower temperatures. The dashed lines in e and f represent mean-field trends for the stochastic variance σ (Supplementary Section X). The error bars represent combined experimental and fitting uncertainties, as detailed in Supplementary Section IX.
While we observe a slight asymmetry in intensities in Fig. 1e, the overall elongated shape at high doping is clearly not captured by either conventional level crossing (Fig. 2a) or anti-crossing (Fig. 2b). Instead, we find that the experimental data are well represented by a model that incorporates ensemble averaging over the coupling \({\mathcal{W}}\), treated as a random, static variable distributed as
$$\langle {\mathcal{W}}\rangle ={{\mathcal{W}}}_{0},\qquad \updelta {\mathcal{W}}=({\mathcal{W}}-{{\mathcal{W}}}_{0})\in [-\sigma ,\sigma ].$$
(2)
Here, \({{\mathcal{W}}}_{0}\) is the mean coupling strength, while σ encodes the variance. The corresponding simulated absorption map (Supplementary Section VII), shown in Fig. 2c, qualitatively agrees with Fig. 1e, capturing two distinctive features: (1) a near-equal intensity distribution between the upper and lower interlayer exciton branches and (2) a plateau-like flattening of the signal along Ez = 0. For this reason, the elongated shape in Fig. 1e is further referred to as stochastic anti-crossing. We emphasize the importance of the static character of the random coupling \({\mathcal{W}}\). If \({\mathcal{W}}\) were instead a time-dependent Markovian variable, its effects would be fully accounted for through a modification of the decay rates γT and γB (Supplementary Section VII).
Using the model in equations (1) and (2), we analyse the experimental data obtained under a variety of different conditions including different temperatures and dopings. Specifically, we simultaneously fit the full reflectance maps (Fig. 1e) with a few-parameter model (Supplementary Section IX), which incorporates substrate reflectance effects and characterizes the interlayer excitons via six parameters: \({{\mathcal{W}}}_{0}\), σ, γ = γT = γB, d = dT = dB, dz and ω0, which is the bare interlayer exciton energy at Ez = 0. The density and temperature behaviour obtained from this analysis, shown in Fig. 2e,f, reveals that the static stochastic variance σ increases with increasing n and decreases with increasing T. The data also point at the development of a non-zero mean coupling \({{\mathcal{W}}}_{0}\ne 0\) (Supplementary Section XIII), which is consistently found to be relatively small \(| {{\mathcal{W}}}_{0}| \ll \sigma\). The mean coupling \({{\mathcal{W}}}_{0}\) roughly follows the trend of σ, but for n ≈ 1.3 × 1012 cm−2 vanishes at T ≈ 40 K, while σ persists up to T ≈ 75 K (Supplementary Section IV).
To gain further insights into the nature of this exciton hybridization, we examine both the valley and spin structure of indirect excitons, illustrated in Fig. 1b. With two inequivalent valleys, associated with the K and \({K}^{{\prime} }\) points of the hexagonal Brillouin zone (BZ), there are four relevant, optically bright interlayer excitons in total: two excitons with opposite out-of-plane dipoles per valley. The 2H-stacked MoS2 homobilayer exhibits \({{\mathcal{C}}}_{3}\)-rotational symmetry, assigning azimuthal quantum numbers (AQNs) to each of its electronic bands (Fig. 1b). The AQNs of the valence bands are zero, allowing holes to tunnel between layers. Conversely, the AQNs of the conduction bands in the same valley are opposite, which is the fundamental reason that prevents electron tunnelling9,12,13 and, thus, naively should prevent interlayer exciton hybridization. The AQNs also dictate the optical selection rules for excitons9,14,15: an electron with AQN +1 (−1) corresponds to an exciton coupling to σ+-polarized (σ−-polarized) light.
One notable feature of MoS2 homobilayers is their small conduction-band spin–orbit splitting of a few millielectronvolts, which could result in spin polarization, but not necessarily valley polarization, of conduction-band electrons via an out-of-plane magnetic field Bz. This expectation is corroborated by our measurements of polarization-resolved reflection contrast spectra of the intralayer A-exciton at Bz = 9 T, Ez = 0 and varying n (Fig. 3c). We observe that the attractive polaron (AP) branch for σ−-polarized light, predominantly sensing spin-↑ electrons, emerges at a higher doping level compared with the σ+-polarized one, which primarily probes spin-↓ electrons5. As a result, for electron densities in the asymmetry region between the two AP onsets (Fig. 3c, dashed green lines), conduction-band electrons become fully spin-polarized. In addition, a previous magnetism study on monolayer MoS2 (ref. 5) suggests that these spin-polarized electrons remain valley-depolarized. For one such representative density n ≈ 1.4 × 1012 cm−2 (Fig. 3c, dashed white lines), we find that the stochastic anti-crossing is robustly present for both light polarizations and for both Bz = 0 (Fig. 3a) and Bz = 9 T (Fig. 3b). Within the error margin of our analysis (Supplementary Section IX), the stochastic variance σ is found to be around 15 meV across all four panels in Fig. 3a,b, while the mean coupling \({{\mathcal{W}}}_{0}\) is nearly zero throughout. A slight departure from this trend is that \({{\mathcal{W}}}_{0}\) develops by at most −2 meV for σ+-polarized light at Bz = 9 T, as indicated by a small intensity asymmetry between the upper and lower exciton branches in Fig. 3b (right). The persistent presence of a large σ nearly independent of Bz indicates that the interlayer exciton hybridization is predominantly agnostic to the electron spin.
Fig. 3: Magnetic field and polarization-resolved properties.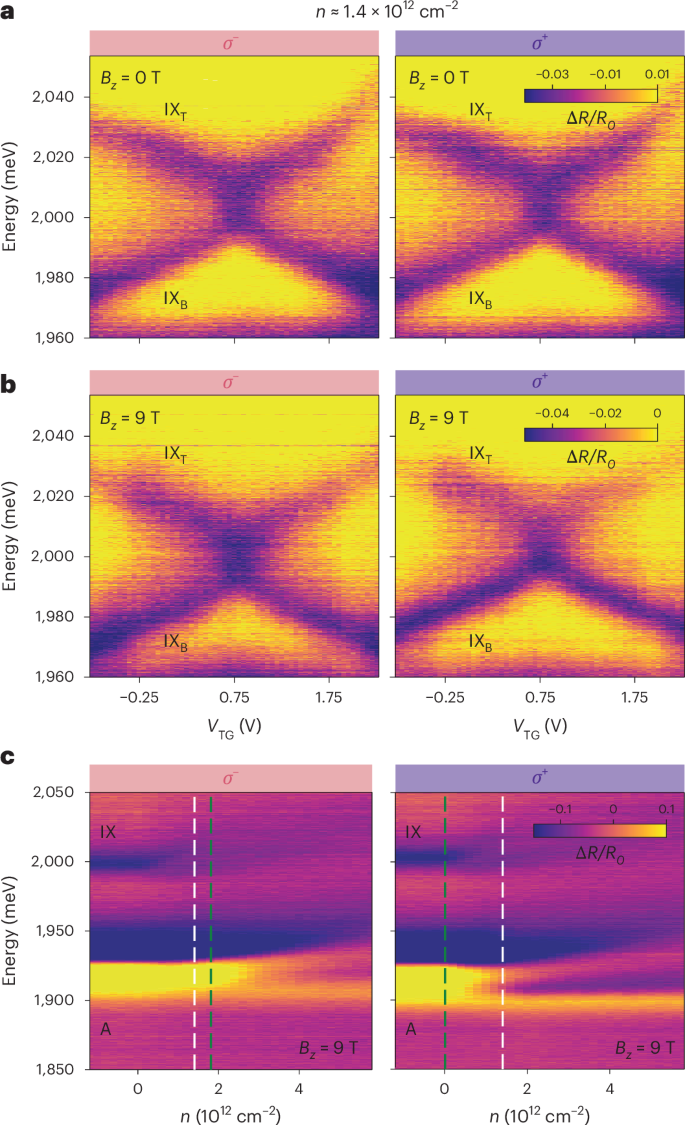
a,b, Electric-field sweeps at n ≈ 1.4 × 1012 cm−2 illustrate the similar appearance of the stochastic anti-crossing for both light polarizations and for both Bz = 0 T (a) and Bz = 9 T (b). At Bz = 9 T, the σ+-measurements reveal a small intensity asymmetry between the lower and upper exciton branches, suggesting a slight development of \({{\mathcal{W}}}_{0}\) for this light polarization. c, At Bz = 9 T and n ≈ 1.4 × 1012 cm−2 (dashed white lines), conduction-band electrons are expected to be fully spin-polarized. This is supported by density sweeps at Ez = 0 of the A-exciton, where the onset of the AP branch for σ−-polarized light (primarily probing spin-↑ electrons) is delayed compared with the σ+-polarized one (essentially sensitive to spin-↓ electrons); these onsets are indicated with dashed green lines.
We now turn to the theoretical interpretation of our observations. The stochastic anti-crossing in Fig. 1e can be attributed to intravalley and/or intervalley interlayer exciton hybridization. The modest asymmetry in the lower and upper branches (associated with a small non-zero mean coupling \({{\mathcal{W}}}_{0}\ne 0\) in the model given by equations (1) and (2)) is probably due to the intervalley scenario, as interlayer excitons within any of the two valleys have opposite AQNs and the optical interference effects that give rise to \({{\mathcal{W}}}_{0}\ne 0\) are suppressed for excitons with opposite polarizations (Supplementary Section VIII). By contrast, the stochastic variance σ ≠ 0 is compatible with both scenarios (Supplementary Section VIII), suggesting that both types of hybridization can play a role.
Hybridization between intervalley interlayer excitons with opposing dipoles is allowed from a symmetry perspective, as these excitons, such as \({{\rm{IX}}}_{{\rm{T}},{{\rm{K}}}^{{\prime} }}\) and IXB,K (depicted in red in Fig. 1b), have the same AQNs. Even without electron doping the sample, these could hybridize with each other via direct Coulomb interactions: either via exciton exchange16,17, expected to be weak because of the reduced transition dipole moment of interlayer excitons compared with intralayer ones, or via a process involving the scattering of the \({{\rm{IX}}}_{{\rm{T}},{{\rm{K}}}^{{\prime} }}\)-exciton electron and hole across the TMD BZ, which is suppressed because it occurs at a large momentum \({\boldsymbol{K}}-{{\boldsymbol{K}}}^{{\prime} }\) and involves electron and hole layer switching (Supplementary Section XI). Thus, such direct coupling is expected to be weak, consistent with \(| {{\mathcal{W}}}_{0}| \lesssim 2\,{\rm{meV}}\) for n = 0 (Fig. 2e). Doping the sample could enhance such hybridization mechanisms via simple effects such as trion formation, polaronic dressing or Fermi sea fluctuations, possibly explaining the emergence of non-zero mean coupling \({{\mathcal{W}}}_{0}\ne 0\) and the density trend in Fig. 2e (such dynamical electron-enhanced exciton hybridization is still expected to be suppressed, consistent with our measurements in Fig. 2e,f, as further discussed in Supplementary Section XI). The intensity asymmetry in Fig. 3b (right) could arise from the presence of doped electrons indistinguishable from the corresponding exciton electron. Increasing temperature weakens polaronic dressing effects18 and increases exciton scattering off phonons19, which reduces exciton wave-function overlaps. Both effects may contribute to explaining decreasing \(| {{\mathcal{W}}}_{0}|\) with increasing T as observed in Fig. 2f.
At the same time, the emergence of the stochastic variance σ involves quasi-static processes, which are beyond the simple dynamical processes mentioned previously, especially given the large values of σ in Fig. 2e,f. Moreover, the effects of quenched disorder or charge traps should be mitigated via electron screening, particularly because strongly interacting regimes in TMDs can be achieved at substantially higher electron densities than in conventional semiconductors4,7,20. Experimentally, we observed σ increases as n increases, which invalidates disorder-induced scenarios. Furthermore, the inversion symmetry of the sample suggests that the system is unlikely to be ferroelectric (a conclusion supported experimentally in Supplementary Section IV), and the absence of amplitude doubling in the stochastic anti-crossing (Fig. 1f) indicates that nonlinearities in Ez are probably not relevant.
Instead, σ could originate from a correlated many-body state that develops an order parameter Δ, in which case the observed stochastic behaviour is attributed to quasi-static spatial fluctuations of this order parameter. In particular, one potential candidate is interlayer electron coherence, corresponding to an exchange instability akin to the typical emergence of ferromagnetism. This correlated state has been proposed theoretically21 and experimentally established in quantum Hall bilayers22,23,24,25,26,27,28,29, where the strong magnetic field quenches the electron kinetic energy and, thus, favours an ordered phase, but it has not yet been conclusively observed at Bz = 0. Such a state requires (1) strong Coulomb interactions \(1\ll{r}_{{\mathrm{s}}}\equiv {m}^{\ast}{{{e}}}^{2}/(4\uppi{\varepsilon}_{0}\varepsilon {\hslash}^{2}\sqrt{\uppi\,n})\) (\({m}^{\ast}\) and ε are the effective electron mass and permittivity of the surrounding medium, respectively), (2) the absence of electron tunnelling and (3) a small interlayer separation lkF ≪ 1 (kF is the Fermi momentum and l ≈ 0.6 nm is the interlayer separation).
Our experimental conditions in the studied MoS2 homobilayer naturally fulfil these stringent prerequisites. First, the large effective mass \({m}^{\ast}\) ≈ 0.7me and the small permittivity of hexagonal boron nitride (hBN), ε ≈ 3.76 (ref. 30), result in rs ≈ 20 for n = 1 × 1012 cm−2 and rs ≈ 11.5 for n = 3 × 1012 cm−2. Second, due to the intravalley conduction-band AQN mismatch in Fig. 1b and as experimentally confirmed in ref. 13, electron tunnelling between the layers is intrinsically absent. Third, we estimate lkF ≈ 0.2 for n = 3 × 1012 cm−2. Finally, by studying samples with varying hBN thickness to modulate the strength of Coulomb interactions, we confirm the Coulomb origin of the studied phenomenon (Supplementary Section III).
The putative emergence of interlayer electron coherence may manifest as the stochastic anti-crossing via a Coulomb-mediated mechanism in Fig. 4b, consistent with and potentially explaining our observations. In conventional semiconductor double-quantum wells, the order parameter is associated with the spontaneous breaking of U(1) symmetry, corresponding to in-plane rotations of the layer pseudospin; the up and down directions of the pseudospin represent the top and bottom layers, respectively (for simplicity, we omit discussion of electron spin). In MoS2 homobilayers, the presence of two valleys enriches this symmetry to U(1) × SU(2), where the SU(2) part is related to valley pseudospin rotations (Supplementary Section XI discusses the approximate nature of this U(1) × SU(2) symmetry in TMDs). This enlarged symmetry places intervalley (Fig. 4a, top) and intravalley (Fig. 4a, bottom) correlations on equal footing (Supplementary Section X). The significance of intravalley correlations, such as \(| \varDelta | {e}^{i\varphi } \approx\)\(\langle {e}_{{\rm{T}}}^{\dagger }{e}_{{\rm{B}}}\rangle \ne 0\) (Fig. 4a, bottom), where eB and \({e}_{{\rm{T}}}^{\dagger }\) are the K-valley electron annihilation and creation operators, respectively, is that they lead to strong Coulomb-mediated electron tunnelling-like processes23,31,32,33,34,35 (Supplementary Section X). In momentum space, these can be expressed as follows (we write only the processes in the K valley):
$$-\sum _{{\mathbf{k}}}{t}_{{\mathbf{k}}}{\hat{e}}_{{\rm{B}},{\rm{K}}}^{\dagger }({\mathbf{k}}){\hat{e}}_{{\rm{T,K}}}({\mathbf{k}})+\,\text{h.c.}\,,$$
(3)
where the coupling constant tk, which provides an effective tunnelling-like rate, is determined by both the order parameter amplitude ∣Δ(r)∣ and phase φ(r). Assuming perfect Hartree–Fock correlations21 and taking into account the ångström-scale interlayer separation between the TMD layers, we estimate tk ≈ 100 meV for n = 2 × 1012 cm−2 (Supplementary Section X). Although this estimate is crude, it underscores the significance of the proposed processes.
Fig. 4: Coulomb-mediated mechanism of interlayer exciton hybridization.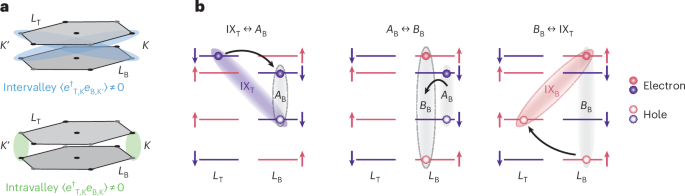
a, The electronic many-body state can exhibit interlayer electron coherence with intervalley (top) or intravalley (bottom) correlations. b, Intravalley coherence leads to an effective order-parameter-induced electron tunnelling-like process (left), resulting in hybridization between IXT- and AB-excitons (shown is the K valley). The AB-exciton couples to the IXB state via exciton exchange (middle) followed by hole tunnelling (right), thereby hybridizing the two interlayer excitons.
This electron tunnelling-like process gives rise to a hybridization of, for example, IXT- and AB-excitons (Fig. 4b, left), with the corresponding coupling estimated to be of the order \({t}_{{{\rm{IX}}}_{{\rm{T}}}\leftrightarrow {{{A}}}_{{\rm{B}}}}\approx 85\,{\rm{meV}}\) for n = 2 × 1012 cm−2 (Supplementary Section X). The AB-exciton is, in turn, coupled to the IXB state via a two-step process shown in Fig. 4b (middle and right), involving exciton exchange36 (Fig. 4b, middle) followed by hole tunnelling9,10 (Fig. 4b, right). This AB–IXB coupling is already established experimentally37, and its strength is estimated to be about \({t}_{{A}_{{\rm{B}}}\leftrightarrow {{\rm{IX}}}_{{\rm{B}}}}\approx 4\,{\rm{meV}}\). Combined, the processes in Fig. 4b result in the hybridization of the two interlayer excitons IXT and IXB, with the coupling strength being of the order of 5 meV for n = 2 × 1012 cm−2 (Supplementary Section X). Although the above analysis relies on two simplifying assumptions—perfect Hartree–Fock correlations and a perturbative approach to relating the electronic order parameter to interlayer exciton hybridization—the estimated number is comparable to the measured values in Fig. 2e. Finally, the exciton exchange step in Fig. 4b (middle) involves flipping both exciton electron and hole spins, indicating that the proposed mechanism is relevant even when conduction-band electrons are spin-polarized by a magnetic field (Fig. 3), provided the system remains valley-depolarized5.
The corresponding interlayer exciton hybridization \(\updelta {\mathcal{W}}({\mathbf{r}})\) is determined by the interlayer electron coherence ∣Δ(r)∣eiφ(r) and, thus, inherits its spatial inhomogeneities arising from statistical fluctuations of the order parameter phase φ(r). Typically, these fluctuations take the form of vortices; however, in TMDs with the enlarged U(1) × SU(2) symmetry, other meron-like topological defects might be essential38. In our experiment, the coupling \(\updelta {\mathcal{W}}({\mathbf{r}})\) is spatially averaged over the optical spot size of about 0.5 μm. This size is expected to be much larger than the phase coherence length (at low temperatures, it is on the order of the correlation length of the disorder potential39, which we expect to be at most a few hundred nanometres). As a result, upon spatial averaging, the order parameter induced contribution to the interlayer exciton hybridization vanishes \(\langle \updelta {\mathcal{W}}({\mathbf{r}})\rangle =0\) (see also Supplementary Section V, where we experimentally explore optical size effects and argue against the phase coherence as the origin of the mean coupling \({{\mathcal{W}}}_{0}\) in equation (2)). Nevertheless, an appreciable stochastic variance σ in equation (2) can develop because it is essentially determined by the order parameter amplitude ∣Δ(r)∣. The observed behaviour in Fig. 2e,f for σ is consistent with the development of the amplitude ∣Δ∣ as electron density n increases within the range accessible in our experiment (rs ≈ 10–20), and its gradual suppression with increasing temperature T until eventual melting; both these trends are well captured by the mean-field analysis, as indicated by the dashed lines in Fig. 2e,f (Supplementary Section X). Although our study reaches a maximum electron density n of about 3 × 1012 cm−2, further increases in n (decreases in rs) should eventually melt the electron coherence21, an expectation supported by the absence of electron tunnelling observed at rs ≈ 3 (ref. 13).
Our observations open up exciting opportunities for exploring strongly correlated many-body phenomena in bilayer systems, particularly in understanding magnetic exchange instabilities—one of the important challenges in modern condensed matter physics. Experimentally, the challenge lies in controllably entering and probing a strongly interacting regime, while theoretically, the phase diagram for rs ≈ 10–20 (as in our experiment), where the electronic system is between a simple Fermi liquid and crystalline states7,20, is not yet fully understood, with only limited Monte Carlo data. In this context, MoS2 homobilayers offer a key advantage as we can naturally access this strongly interacting regime, while interlayer excitons represent a unique optical probe of pseudospin correlations.
Our observations have close connections with several fundamental many-body phenomena expected in bilayer systems, such as interlayer exciton condensation28,40,41 and interlayer electron superconductivity42. We remark that a small twist between the TMD layers breaks the \({{\mathcal{C}}}_{3}\)-rotational symmetry and gives rise to a small direct electron tunnelling. This tunnelling is expected to stabilize the order parameter phase coherence and lead to more coherent rather than stochastic hybridization between interlayer excitons. In addition, the application of an in-plane magnetic field might enable the exploration of the Pokrovsky–Talapov phase transition43 (Supplementary Section XI discusses that, even without twisting, electron pair tunnelling events can occur, but their role is yet to be fully understood). Furthermore, the TMD valley degree of freedom is expected to enrich the phase diagram compared with conventional semiconductors, as the order parameter is likely to have multiple components (Fig. 4a and Supplementary Section X); understanding the structure of spatial order parameter inhomogeneities and their interplay with disorder warrants further theoretical investigation.
Another exciting avenue for future research is to explore the coherence properties of strongly interacting indirect excitons. Our work demonstrates that these can be substantially influenced by tuning the many-body electron system, potentially enabling novel quantum optics applications. We envision that, similar to the interlayer exciton coupling observed here, electron doping of MoS2 trilayers might lead to the hybridization of quadrupolar excitons10,44, which could have promising applications for sensing in the terahertz domain and quantum information processing45. Further insight into exciton interactions could potentially be gained through time-resolved spectroscopy techniques.