The increasing demand for computational power drives exploration of mixed-precision computing, where lower-precision data formats offer potential performance gains and energy savings, but introduce numerical challenges. Piotr Luszczek, Vijay Gadepally, and LaToya Anderson, along with William Arcand, David Bestor, and William Bergeron, investigate the implications of an extreme form of this approach, split integer emulation of 64-bit floating-point numbers, performed entirely on fixed-point tensor cores. Their work reveals new issues arising in practical applications like dense linear solvers, demonstrating how the extended numerical range of matrix entries impacts both performance and accuracy on modern Hopper GPUs. This research provides crucial insights into the trade-offs between precision and efficiency in high-performance computing, paving the way for more effective utilisation of emerging hardware accelerators.
Mixing precisions for performance is becoming increasingly common as modern hardware accelerators incorporate new, lower-precision data formats. Utilizing these formats offers potential gains in performance and energy efficiency, but introduces numerical challenges not present in standard floating-point formats. This work explores the emulation of 64-bit floating-point arithmetic using fixed-point tensor core units, taking this concept to an extreme, and investigates the issues this emulation faces when applied to practical dense linear solvers, demonstrating the effect of extended numerical ranges within matrix entries.
Lower Precision Matrix Computation and Stability
This research focuses on improving the performance and reliability of matrix computations, a cornerstone of High-Performance Computing. Scientists are investigating techniques to mitigate rounding errors and enhance the stability of matrix operations, including utilizing error-free transformations, such as the Ozaki scheme, to perform matrix operations without accumulating errors. The team also explores mixed-precision arithmetic, balancing performance and accuracy by using different precision levels for different parts of a computation, and investigates integer matrix multiplication as a means to achieve high performance and potentially improve accuracy. To rigorously evaluate algorithms, researchers developed methods for generating test matrices with specific properties, like maximum condition number, and implemented a split integer approach, representing floating-point numbers with integers and performing computations accordingly.
Leveraging tensor cores for accelerated matrix computations is another key element of their work, demonstrating significant improvements in accuracy and performance, showing scalability to large-scale HPC systems and improved reliability through error-free transformations and careful data generation. Detailed performance analysis, including comparisons with standard cuBLAS implementations, further validates these findings. The development of a robust methodology for generating test matrices with specific properties is a notable achievement, and validating these techniques on real-world HPC systems demonstrates their practical applicability. Understanding error-free transformations, mixed-precision arithmetic, and tensor cores is crucial for pushing the boundaries of HPC by developing more accurate, reliable, and efficient matrix computations, addressing a critical challenge in scientific computing: achieving high performance while maintaining numerical accuracy. The techniques developed have the potential to improve a wide range of applications, including scientific simulations, machine learning, and data analysis, with future research directions including applying these techniques to different algorithms, developing automatic tuning methods, improving fault tolerance, integrating with machine learning frameworks, and investigating energy efficiency.
Fixed-Point Emulation Achieves FP64 Precision
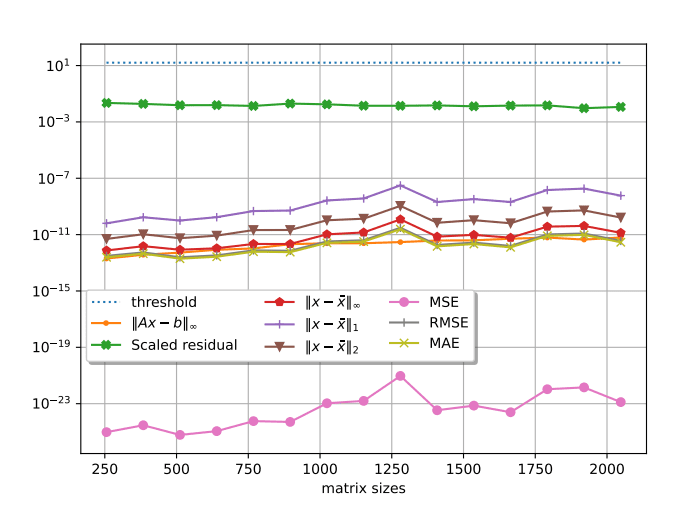
Scientists have successfully emulated 64-bit floating-point precision using fixed-point tensor core units, demonstrating a novel approach to high-performance computing. This work investigates the challenges and opportunities presented by utilizing lower-precision data formats on modern hardware accelerators, specifically focusing on emulating 64-bit floating-point arithmetic with 8-bit integer operations. Extensive numerical tests reveal the impact of matrix entry ranges on the accuracy of this emulation, particularly within dense linear solvers. Researchers conducted experiments with matrices generated using a parametric formula, the ParaWilk formulation, and observed that up to seven splits were required to achieve passing scaled residual values for correctness, reaching 39.
1 for certain parameter sets. The team discovered that generating matrices with only positive random entries, skewed towards larger values, improved numerical stability, and that scaled residual values varied significantly with different parameter settings, ranging from 17. 3 to 40. 6, demonstrating the potential for tailoring matrix properties to optimize accuracy. Performance evaluations conducted on NVIDIA Hopper GPUs with over 55 Tflop/s of FP64 performance show the feasibility of this approach, with simplifying the implementation to focus on matrix products maximizing the influence of the INT8 splitting emulation and achieving higher performance.
Emulating FP64 with INT8 Tensor Cores
This research demonstrates a novel approach to emulating high-precision, 64-bit floating-point calculations using lower-precision, 8-bit integer tensor cores, a technique increasingly relevant with modern hardware accelerators. The team investigated splitting calculations into multiple components and mapping them onto separate compute units to effectively recreate the accuracy of FP64 using INT8 operations. Extensive numerical tests reveal the impact of extended numerical ranges within matrices during this emulation process, particularly when scaling input sizes on Hopper GPUs. The findings are significant because they address a growing imbalance in computational power between FP64 and INT8 formats, exemplified by the NVIDIA Blackwell architecture where FP64 performance has decreased while INT8 capabilities have dramatically increased. By successfully emulating FP64 using INT8, this work offers a pathway to leverage the substantial performance gains available in modern hardware for applications traditionally reliant on high-precision calculations. The authors acknowledge limitations related to the complexity of managing rounding errors inherent in splitting schemes and the need for careful consideration of numerical stability, with future research directions including exploring methods to optimise the splitting process and further refine techniques for mitigating rounding errors to enhance the accuracy and efficiency of FP64 emulation on emerging hardware platforms.
👉 More information
🗞 Performance and Numerical Aspects of Decompositional Factorizations with FP64 Floating-Point Emulation in INT8
🧠 ArXiv: https://arxiv.org/abs/2509.23565