An analog photoelectronic reservoir computing system
Figure 1a shows the dynamic vision processing in the human visual system. Visual inputs are initially detected by the retina located at the bottom of the eyeballs, which would trigger the action potential by ganglion cells through the transmission of bipolar cells. The encoded information is then transmitted to the thalamus15,16,17. Cells in thalamus with receptive fields are layered and in the form of populations, enabling the feature extraction of visual information. Features like edge, angle, orientation, and direction of motion can be extracted before entering the visual cortex. Through spike precoding by multilevel neuronal populations with receptive fields within the retina, intellectual activities such as recognition and decision-making can be finally realized in the human brain. The powerful and energy-efficient human visual system for dynamic vision processing has inspired us to conceptualize a neuromorphic visual system featuring receptive fields and a spike encoding scheme. Hence, a bioinspired in-materia analog photoelectronic reservoir computing (Alpho-RC) system was built for dynamic vision processing.
Fig. 1: A bioinspired in-materia analog photoelectronic reservoir computing (Alpho-RC) system.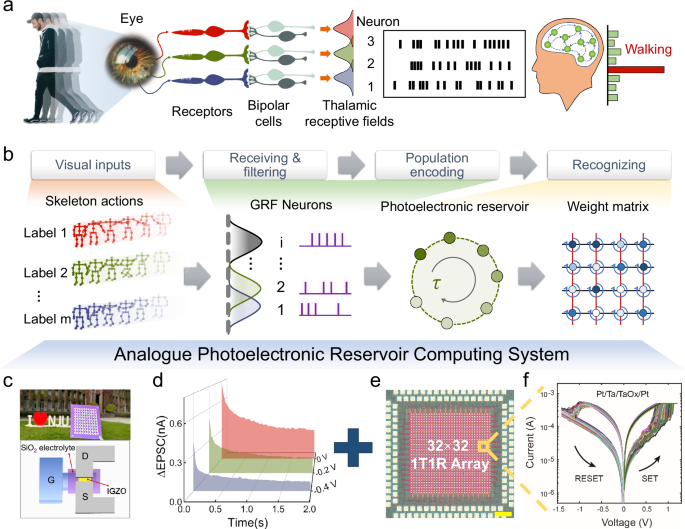
a Conceptual diagram of dynamic vision processing in human visual system. The walking man and eye are reproduced with permission from Pixabay. b Schematic diagram of calculation processes in Alpho-RC system. c Photograph of EDL-coupled IGZO photoelectronic transistor array and schematic diagram of IGZO transistor structure. d The response and relaxation behaviors of EDL-coupled IGZO photoelectronic transistor in response to a light pulse (38 ms, 2.95 nW·μm–2) under different gate bias conditions (−0.4, −0.2, and 0 V, respectively). e A micrograph image of a 32 × 32 1T1R array (scale bar: 200 μm). f 100 cycles of I-V sweeps of a Pt/Ta/TaOx/Pt memristor in the array.
Figure 1b shows the schematic diagram of such Alpho-RC system. The data modes of human action are mainly divided into visual modes (RGB, Depth, Skeleton and so on) and non-visual modes (Inertial acceleration data, Wireless-transmission signal and so on)18,19,20,21,22. Among them, the visual mode is more in line with human intuitive feelings. Compared with other visual modalities, a 3D skeleton frame as a topological form of joints and skeletons abstracts the human body into a three-dimensional coordinate space, which tends to be more robust in complex environments. Therefore, 3D skeleton-based human action frames are selected as visual input in the system.
The core elements of spike encoding scheme are neurons with GRF without additional filtering process. In biology, stimuli carried essential features are selectively responded by neurons with overlapped and graded receptive fields, and the varied levels of features thus can be extracted in different neural pathways23. Stimulus can significantly fire at the neurons with proper receptive field, and might be silence in other neurons. Such biological encoding mechanisms enable only a small size of data being processed by the central nervous system. In contrast, running machine learning algorithms in a digit system always requires complex feature extraction steps, which lead to a huge computational burden24. In Alpho-RC system, several GRF neurons are defined as one population encoder, which is corresponding to population transistor consisting of electric-double-layer (EDL) coupled IGZO photoelectronic transistors. EDL coupled IGZO transistors have been demonstrated with photoelectronic synaptic plasticity by gate voltage tunability based on persistent photoconductivity (PPC) effects and proton relaxation dynamics25,26,27. Figure 1c shows the photograph of photoelectronic transistor array and schematic diagram of IGZO transistor structure. Details on transistor array fabrication, basic properties and hardware operation system can be found in “Methods” section and Supplementary Figs. 1–9. The response and relaxation behaviors of the EDL-coupled IGZO photoelectronic transistor in response to a light pulse (38 ms, 2.95 nW·μm–2) under different gate bias conditions (–0.4, –0.2, and 0 V, respectively) has shown in Fig. 1d. The electrons generated by PPC effect would increase the channel conductance transiently. When a light stimulation ends, accumulated electrons would recombine gradually with the triggered oxygen vacancies within a certain time. As a consequence, the channel conductance gradually decreases, exhibiting relaxation characteristics. A negative gate voltage would decrease the channel conductance through the EDL coupling, leading to a decreased decay time. The decrement is positively related to the absolute value of the negative gate voltage (detailed information can be found in Supplementary Note 1). By applying varied gate biases that are corresponded to GRF neurons with different distribution centers, current states of the transistor are tuned in response to the encoding pulses from GRF neurons, mapping the visual input information to the high-dimensional space in turn.
Physical reservoir computing (PRC) based on material intrinsic dynamics has been demonstrated with excellent time signal processing capabilities, which is selected as the calculation method in Alpho-RC system28,29,30. Obtained response currents by population transistors are used as reservoir states for training output weights. Compared with the processing path by single device in traditional PRC systems, such receptive field-enhanced population encoding mechanism increases the information processing capacity by providing multiple parallel information processing ports. Meanwhile, no additional feature extraction is required to apply on skeleton sequences, through such bioinspired in-materia reservoir computing framework. However, the feature extraction is still required for skeleton frames in vast number of reported algorithms. For example, while facing the skeleton-based action recognition tasks, feature set including spatial-domain-feature (relative position, distances between joints, distances between joints and lines) and temporal-domain-feature (joint distances map, joint trajectories map) needs to be extracted prior to the training of neural networks31.
The output layer was also implemented in a 32 × 32 1T1R array for fully hardware implementation of the bioinspired in-materia reservoir computing system, as shown in Fig. 1e (the detailed device structure and fabrication can be found in Supplementary Fig. 10 and “Methods” section). TaOx-based memristors were integrated on top of a foundry-made complementary-metal-oxide-semiconductor (CMOS) chip with silicon-based selecting transistors and fan-outs (the detailed characterizations and the setup of hardware operation system can be found in Supplementary Figs. 11–14). The memristors demonstrated good switching uniformity and stability for reliable programming of offline-trained weights for human action processing (Fig. 1f). Our analog photoelectronic reservoir computing system is built based on the IGZO transistors for reservoir states collection and the TaOx-based memristors for matrix operations.
The bioinspired in-materia reservoir computing framework
The dimensionality enhancement process of the photoelectronic reservoir in Alpho-RC system contains time multiplexing and GRF encoding. Time multiplexing with mask matrixes is a common method in PRC systems, which solves the difficulty of interconnecting physical device nodes based on the concept of delayed nodes30. Figure 2a shows the calculation flow of time multiplexing on original action skeleton information. Firstly, K body joint points with coordinate information (xi, yi, zi) are collected from a subject, which maps the human body’s action posture into a three-dimensional coordinate space. Therefore, temporal changes of the K joint coordinate positions from frame-to-frame can describe the dynamic change of an action. 3D joint coordinates of each frame are written as one-dimensional sequence vector [x1 y1 z1 x2 y2 z2 …… xK yK zK] or [J1 J2 …… JK] according to the order of the skeleton joints. In this case, the dynamic coordinates of a complete the action (Act, with a size of 3·K×N) can be represented by:
$${Act}=[ \, \, {{{{\boldsymbol{J}}}}}_{{{{\bf{11}}}}}\,{{{{\boldsymbol{J}}}}}_{{{{\bf{12}}}}}\ldots {{{{\boldsymbol{J}}}}}_{{{{\bf{1}}}}{{{\boldsymbol{k}}}}};\ldots \ldots ;{{{{\boldsymbol{J}}}}}_{{{{\boldsymbol{n}}}}{{{\bf{1}}}}} \, {{{{\boldsymbol{J}}}}}_{{{{\boldsymbol{n}}}}{{{\bf{2}}}}}\ldots {{{{\boldsymbol{J}}}}}_{{{{\boldsymbol{nk}}}}};\ldots \ldots ;{{{{\boldsymbol{J}}}}}_{{{{\boldsymbol{N}}}}{{{\bf{1}}}}} \, {{{{\boldsymbol{J}}}}}_{{{{\boldsymbol{N}}}}{{{\bf{2}}}}}\ldots {{{{\boldsymbol{J}}}}}_{{{{\boldsymbol{Nk}}}}}]$$
(1)
where n (n = 1, 2, …, N) is the frame order of action and N is the total number of frames consisting of an action. The dynamic change of the 3D joint coordinates (ΔAct, with a size of 3·K × N) can be represented by the subtraction of the action matrix and the first sequence of the action:
$$\varDelta {Act}=[{{{\bf{0}}}}\,{{{\bf{0}}}}\ldots {{{\bf{0}}}};\ldots \ldots ;{{{\boldsymbol{\Delta }}}}{{{{\boldsymbol{J}}}}}_{{{{\boldsymbol{n}}}}{{{\bf{1}}}}} \, {{{\boldsymbol{\Delta }}}}{{{{\boldsymbol{J}}}}}_{{{{\boldsymbol{n}}}}{{{\bf{2}}}}}\ldots {{{\boldsymbol{\Delta }}}}{{{{\boldsymbol{J}}}}}_{{{{\boldsymbol{nk}}}}};\ldots \ldots ;{{{\boldsymbol{\Delta }}}}{{{{\boldsymbol{J}}}}}_{{{{\boldsymbol{N}}}}{{{\bf{1}}}}} \, {{{\boldsymbol{\Delta }}}}{{{{\boldsymbol{J}}}}}_{{{{\boldsymbol{N}}}}{{{\bf{2}}}}}\ldots {{{\boldsymbol{\Delta }}}}{{{{\boldsymbol{J}}}}}_{{{{\boldsymbol{Nk}}}}}]$$
(2)
where ΔJnj is the change of coordinates (ΔJnj=Jnj-J1j), and j is the number of joint (j = 1, 2,…, K). Figure 2b shows examples of ΔActn (ΔActn = [ΔJn1ΔJn2… ΔJnK]) corresponding to the action “openarm” shown in Fig. 2a. After that, ΔAct is mapped into high dimensional space by multiplying mask matrixes. The mask matrix is a randomly generated two-dimensional matrix consisting of 1 and -1, with a size of 3·K × M (M is the mask length). At nth frame of the action, the ΔActn (1 × 3·K) is multiplied by the mask matrix, generating virtual nodes (Vn = [Vn1 Vn2 … VnM]) with a size of 1×M. In this case, the ΔAct is mapped to a higher dimensional matrix noted as PreIn matrix (1×M·N):
$${PreIn}=[{{{{\boldsymbol{V}}}}}_{{{{\bf{1}}}}}{{{{\boldsymbol{V}}}}}_{{{{\bf{2}}}}}\ldots {{{{\boldsymbol{V}}}}}_{{{{\boldsymbol{N}}}}}]$$
(3)
Fig. 2: The Gaussian receptive field based encoding and photoelectronic reservoir computing.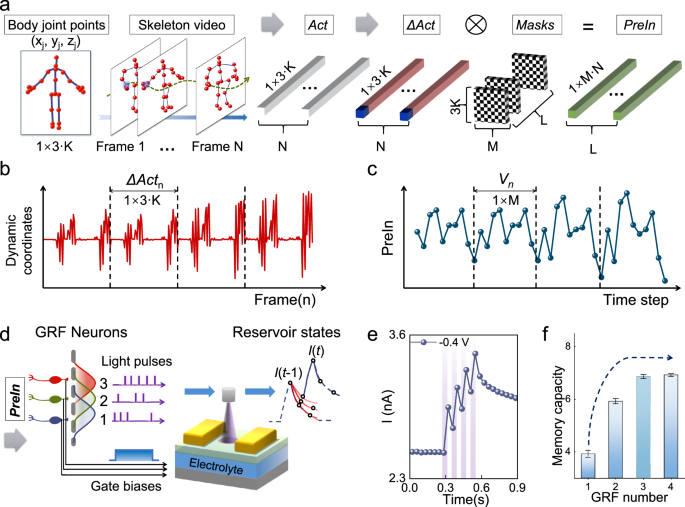
a The calculation flow of time multiplexing on original action skeleton information in photoelectronic reservoir computing. b Examples of ΔActn corresponding to the action “openarm” in (a). c An example of PreIn corresponding to ΔActn in (b) with a mask matrix (M = 10). d The converted light pulse trains from spike trains of Neuron #1, #2, and #3 and are applied on one population transistor consists of three IGZO-based photoelectronic synaptic transistors with different modulated biases. e The response current of transistor with gate bias of −0.4 V to four consecutive light pulses (38 ms ON and 38 ms OFF). f MC values with different numbers (1, 2, 3, and 4) of Gaussian receptive fields. The error bars represent the standard deviation of five independent tests.
Figure 2c shows one example of PreIn corresponding to ΔActn in Fig. 2b with a mask matrix (M = 10).
Then, the PreIn corresponding to a completed action is encoded to spikes through GRF neurons. The Gaussian receptive fields of the Alpho-RC system are set based on the intensity of PreIn, which is inspired from encoding process of biological systems and spiking neural networks (SNN)32. For every input, the output through ith receptive field yields the Gaussian distribution (Gi) with a mean value of μi and deviation of σi. So, the output (Gi(A)) is dependent on the distance between input intensity (A) and μi:
$${G}_{i}(A)=\frac{1}{\sqrt{2\pi {\sigma }_{i}^{2}}}\exp \left(-\frac{{\left(A-{\mu }_{i}\right)}^{2}}{2{\sigma }_{i}^{2}}\right)$$
(4)
In this case, each input can trigger an output through all receptive fields, while the outputs are different. The GRF neuron would trigger a firing spike only if the output from the corresponding receptive field is the largest. Here, several neurons (Neuron #1, #2, … #i) corresponding to receptive fields (GRF #1, #2, … #i) are defined as one population encoder which is used for spike encoding. The σ of neurons is uniformly set to the standard value of 1, and the centers (μ1,μ2, …μi) of GRFs are set by:
$${{{\mu }}}_{i}={A}_{\min }+\frac{{A}_{\max }-{A}_{\min }}{m+1}\times i$$
(5)
where Amin and Amax represent the minimum value and the maximum value of input intensity (A), m is the number of GRF neurons. To facilitate data processing, we perform a normalization process, so that the amplitude of PreIn is limited between -1 and 1. Accordingly, Gaussian centers are set by:
$${{{\mu }}}_{i}=\frac{2}{m+1}\times i-1$$
(6)
The normalized PreIn of a completed action is then converted into spike trains (Spike-input) through the aforementioned GRF-based population encoding scheme. The spike trains from Neuron #1, #2, … #i are converted into light pulse trains (405 nm, 2.95 nW·μm–2) and applied on one population transistor consisting of EDL-coupled IGZO photoelectronic transistors under different gate bias conditions (as shown in Fig. 2d). Each light pulse corresponding to firing spike is set to 38 ms ON, and stationary state without firing spike is set to 38 ms OFF. Thus, the time step between each node of PreIn is fixed, and the triggered channel currents of population transistor at each time step are collected as reservoir states. Relaxation characteristic curves are used as the activation function. As mentioned before, the characteristics are varied in transistors with different gate biases, which increase the richness of reservoir states. Figure 2e shows the response current of transistor with gate bias of -0.4 V to four consecutive light pulses (38 ms ON and 38 ms OFF). Supplementary Figs. 15, 16 show the device responses under different gate bias voltages to light pulse trains of different frequencies. Specific model fitting and calculation details can be found in Supplementary Fig. 17, Fig. 18, Table 1 and Note 2. L population encoders are connected in parallel to build a large parallel RC system. Each population encoder is responsible for encoding different PreIn, which is generated with L different mask matrixes parallelly. Thus, L population transistors with 3×L devices in arrays are used to obtain parallel reservoir states and 3×L×M reservoir states are recorded per frame. Supplementary Video I shows the aforementioned spike encoding and reservoir states collection processes.
Finally, the reservoir states are collected for training and testing. During the training process, only the output weights (Wout) connected to the output layer are needed to be trained. The collected reservoir states are subjected to a one-step linear regression along with labels to obtain the desired weights33. The resulting output weights are multiplied with reservoir states collected from the testing process, and the output label is obtained based on the winner-take-all method34. Supplementary Fig. 19 shows the specific procedures, and detailed calculation procedures can be found in “Methods”.
Memory capacity (MC) is a task-independent evaluation index of reservoir computing, which represents the ability of reservoir states to preserve input information previously29,35. We evaluated the MC metrics of the bioinspired reservoir with different numbers (1, 2, 3, and 4) of GRF neurons. During encoding, the Gaussian centers were also sequentially set according to Eq. (6). Population encoders with different GRF neuron numbers (1, 2, 3, and 4) are corresponding to population transistor consisting of different amounts of EDL-coupled IGZO photoelectronic transistors with fixed VGS of 0 V, –0.2 V/0 V, –0.4 V/–0.2 V/0 V, –0.8 V/–0.4 V/–0.2 V/0 V, respectively. Specific calculation process of MC can be found in Supplementary Note. 3. As shown in Fig. 2f, high MC value (~6.9) is obtained by three receptive fields with filtering and encoding. This should be due to the enriched reservoir states rendered by multiple GRF neurons. When encoding number is more than three, the MC value is almost remained. However, the greater number of GRF neurons, the larger the data scale is required, which would increase the computational burden on the following steps. Therefore, three GRF neurons are fixed as one population encoder and one population transistor is fixed of three EDL-coupled IGZO photoelectronic transistors with fixed VGS of –0.4 V, –0.2 V, 0 V, respectively in the bioinspired reservoir.
Human action recognition tasks based on standard datasets
The UTD-MHAD dataset contains 27 classes of human actions collected from 8 subjects36. Each skeleton frame consists of dynamic coordinates of 20 body joints. Figure 3a shows examples of color images and skeleton frames corresponding to a home-made action “High throw” (left panel) and an action “Basketball shoot” (right panel) in UTD-MHAD dataset. Color images and skeleton frames of home-made action were collected by authors through a mobile phone camera and a Kinect camera, respectively. In the UTD-MHAD standard dataset test, we randomly selected 30 samples of each action class, and divided them into training set and testing set at a ratio of 9:1. Specific encoding processes can be found in Supplementary Fig. 20. Figure 3b shows partial time sections of reservoir states triggered by the light pulse trains and collected from the IGZO synaptic transistors. Different mask matrixes were used and the optimized performance was achieved with M = 30 and L = 30. After training and testing processes, the recognition rate was calculated by counting the recognition results of the entire data in the testing set. Repeated random subsampling validation method was used by ten times to enhance the reliability of results37. The average of ten results was used as the final system recognition result.
Fig. 3: Recognition results and analysis on standard dataset tests based on bioinspired reservoir computing paradigm.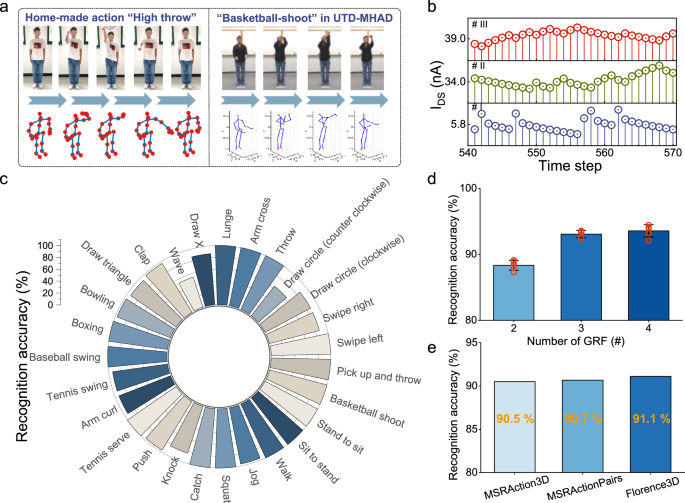
a Examples of digital images and skeleton frames corresponding to a home-made action “High throw” and an action “Basketball shoot” in UTD-MHAD dataset, where the digital images and skeleton frames of home-made action were collected by authors through a mobile phone camera and a Kinect camera, respectively. Digital images and skeleton data in UTD-MHAD dataset is reprinted with permission36, Copyright 2015, IEEE. b The partial time sections of reservoir states triggered by the light pulse trains and collected from the IGZO synaptic transistors. c Specific recognition results with bioinspired reservoir computing on UTD-MHAD dataset. d The recognition accuracies of UTD-MHAD dataset standard test with different numbers (2, 3, and 4) of Gaussian receptive fields. The error bars represent the standard deviation of five independent tests. e Recognition accuracies achieved on different validation datasets with bioinspired reservoir computing.
Figure 3c shows the recognition results with respect to UTD-MHAD dataset. The recognition rate based on all action classes reaches 93.58%. As can be seen, most actions can be well recognized and only a few actions like “Wave” are with relatively low recognition accuracy. Among all action classes, the system achieves an excellent recognition rate of 100% on 14 classes, and high accuracy (≥ 90%) on 21 classes. This shows that our system can well distinguish multiple types of complex action processes.
The recognition tasks were also verified with different numbers (2, 3, and 4) of Gaussian receptive fields as shown in Fig. 3d. The Gaussian centers were also sequentially set according to Eq. (6). As shown in Fig. 3d, high recognition accuracy (>90%) on UTD-MHAD dataset is obtained by three receptive fields. This is consistent with the results of MC metrics in Fig. 2f. We further investigated the effect of standard deviation of Gaussian receptive fields on the recognition results. Our results indicate that σ can have a slight effect on recognition accuracy. By varying σ from 0.1 to 10, the maximum variation on recognition accuracies is only 1.11% (Supplementary Fig. 21). Computation complexity can be reduced based on such GRF encoding scheme. On the one hand, the scale of our network parameters are almost 2 orders of magnitudes smaller than previous machine learning algorithms (e.g., ResNet18) regarding UTD-MHAD dataset (detailed illustration can be found in Supplementary Fig. 22)38,39,40. On the other hand, multiple training iterations are not required in our training process, and only one-step linear regression is needed, which also reduces the computation complexity. Our results indicate that GRF-based preprocessing is vital important for implementing the human action recognition by reservoir computing, and the very limited number of GRF neurons can have a significant improvement in recognition accuracy.
We further verified this bioinspired reservoir computing paradigm on human action recognition tasks by three datasets of MSR Action3D, Florence 3D, and MSR Action Pairs. The MSR Action3D dataset contains 20 classes of skeleton-based action frames, and 20 skeleton joints’ coordinates are recorded per frame41. The dataset was used for verification, where 90% samples were chosen randomly for training and the rest for testing. A high recognition rate of 90.50% is obtained (Supplementary Fig. 23). Florence 3D dataset contains 9 action classes, and 15 skeleton joints’ 3D coordinates are recorded in each frame42. Our system can identify 91.11% of the testing samples successfully (Supplementary Fig. 24). The actions in MSR Action pairs dataset are in paired with similar action trajectories43. This makes it difficult to recognize actions in a pairwise relationship. As shown in Supplementary Fig. 25, 12 action classes can be well distinguished with an average recognition accuracy of 90.67%. Specific parameters of bioinspired reservoir on three dataset standard tests can be found in Supplementary Table 2. Repeated random subsampling validation method was applied by five times in the three tasks to enhance the reliability of results. In addition, such bioinspired reservoir computing paradigm can be also applied for high-precision and multi-type action recognition task based on depth images in videos (achieving an accuracy of 92.35% on 27 labels, and the calculation process can be found in Supplementary Note 4). As high recognition accuracies (>90%) can be achieved on different validation datasets as shown in Fig. 3e and Supplementary Fig. 26, our system exhibits remarkable versatility and fault tolerance for human action recognition.
Recognition of falling behaviors based on analog system
The conceptual diagram of our Alpho-RC system for real-world human action processing tasks is shown in Fig. 4a. Skeleton frames of daily activities collected by the Microsoft Kinect camera are the original input, and the Gaussian receptive field based encoding mechanism is implemented. During the training process, currents obtained by population transistors in response to encoding pulse trains are used as reservoir states for training output weights. During the testing process, resulting output weights are mapped by 1T1R array, and output currents of testing action sample are obtained. The video processing tasks are mostly involved in human action recognition and prediction. Human action recognition tasks usually focus on completed actions, and achieve classification purposes by learning the entire processes of actions. However, in actual scenarios, it is often necessary to achieve early classification and prediction before action ends, such as predicting and alerting before falling behaviors are completed44. Purpose of the prediction task is to output the corresponding action label by using only the early frame sequences for inferencing.
Fig. 4: Recognition of falling behaviors based on Alpho-RC system.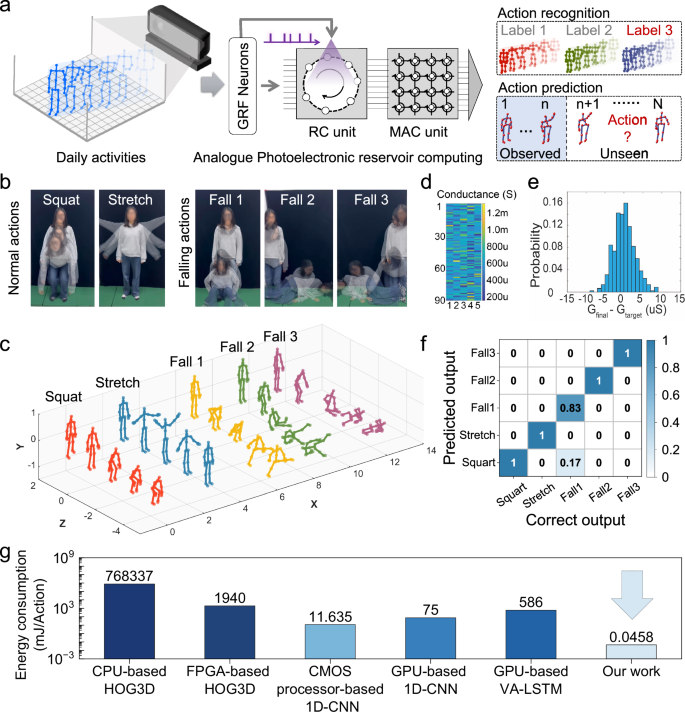
a The computational architecture schematic diagram of Alpho-RC system for human action recognition and prediction. b Examples of five actions including two normal actions (squat and stretch) and three falling actions (fall down, fall to the left and fall to the right) recorded by a mobile phone camera. c Examples of action skeleton frames corresponding to five actions. d Device conductance from 200−1300 µS mapped from the numerical weight values. e The write error tolerance of ±1% during mapping program. f Recognition accuracy of 96.67% obtained by memristor-based output layer. g Comparison of energy consumption per action among Alpho-RC system and algorithms based on various advanced processors.
Falling behaviors as common events in real life often involves potential health risks. For example, elderly people living alone and children are more likely to suffer physical injuries if they fall, thus affecting their health. Effectively identify falling behaviors from normal behaviors is crucial to the safety of both young and old45,46. A home-made 3D skeleton-based falling dataset was used for verifying the efficacy of such system for dealing with real-world tasks. Such dataset including two normal actions (squat and stretch) and three falling actions (fall down, fall to the left and fall to the right) was collected and built by both digital and Kinect camera. Figure 4b shows examples of the five actions recorded by a mobile phone camera. Figure 4c shows examples of action skeleton frames recorded by a Kinect camera correspondingly. Specific demonstration of skeleton frames can be found in Supplementary Video II. The collection details can be found in the “Methods”. Here, the recognition on such home-made falling dataset was implemented by our Alpho-RC system. The 90% of action samples in the dataset were randomly selected as the training set, and the output weights were obtained by noise-aware linear regression training method (M = 6, L = 5). The detailed training process can be found in Supplementary Note. 5. The offline-trained weights were then programmed into the memristor cells in the 1T1R array. The numerical weight values were firstly mapped to device conductance from 200-1300 µS (Fig. 4d) and then programmed into the array using a write-and-verify programming scheme. Detailed reliability data of the hardware setup can be found in Supplementary Figs. 27, 28. Good programming accuracies were achieved with write error tolerance of ±1% (Fig. 4e). The memristor-based output layer successfully classified five actions with recognition accuracy of 96.67% (as shown in Fig. 4f), which is close to software simulations of 98.33% (as shown in Supplementary Fig. 29). The successful demonstration of human action recognition in the hardware based bioinspired in-materia reservoir computing paves the way for energy-efficient edge computing applications. Our Alpho-RC system was also applied for human action prediction. Only the observed frames were fed into the photoelectronic reservoir for predication. Here, the ratio between the number of observed frames and the frames of the completed action is defined as observation ratio. As shown in Supplementary Fig. 30, the prediction accuracies are plotted as function of the observation ratios with respect to home-made falling dataset. The prediction accuracies are larger than 80% with the observation ratio higher than 50% and larger than 90% with the observation ratio higher than 70%. Such results indicate our system can achieve excellent prediction results, verifying the capability of both human action recognition and prediction.
Finally, the energy efficiency of such system is evaluated by calculating the energy consumption corresponding to processing one completed action. As mentioned before, no complex filtering process is required for the feature extraction of every action. The most energy consumption before the training of weights connected to the output layer should be attributed to encoding process and the current flow through transistors. The energy consumption for processing an action by our system is only ~45.78 μJ (detailed estimation can be found in experimental section). However, feature extraction is required in most previous software-based methods, which dramatically increases the floating-point operations and the energy consumption in turn. The comparison of energy consumption is summarized in Fig. 4g. Our Alpho-RC system is at least two orders of magnitude lower than that of CMOS-based processors including CPU, FPGA, and GPU47,48,49. We also compared the reported physical reservoir computing architectures for human action recognition (Supplementary Table 3), achieving largest type number of human action classification13,50,51,52.