We highlight how an abstract piece of condensed-matter physics — the fractional quantum Hall effect — may be ideally placed to implement quantum computers.
One of the few subfields of physics that routinely breaks though into public consciousness is quantum computing. Quantum computation offers either tantalizing options for speeding up certain types of computation, or a terrifying vision where current-day digital security is compromised, depending on one’s outlook.

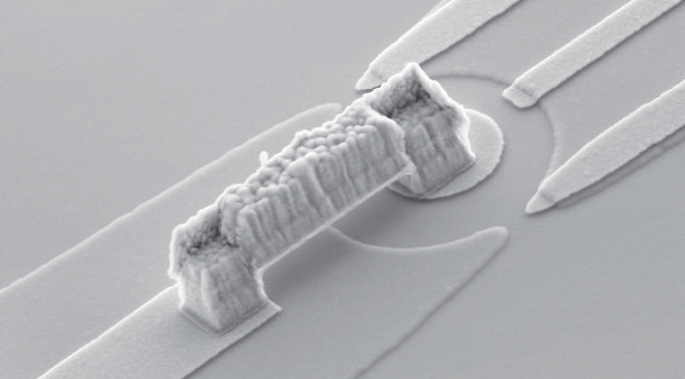
Credit: Moty Heiblum and Bikash Ghosh
Unfortunately, the qubits used to build these devices are never perfect. The imperfect qubits introduce errors into any computation and limit the potential utility of these machines. One way to combat this is to build logical qubits that utilize many physical qubits operating with error-correcting codes, but this has the substantial downside of increasing the number of physical qubits required.
Another possibility is to implement topological quantum computing, where the qubits are encoded in a protected degree of freedom that is — at least to a large extent — unaffected by external perturbations and therefore free from errors. There are many potential platforms for doing this, but all require the presence of exotic entities known as anyons: emergent quasiparticles that are neither fermions nor bosons. Additionally, the anyons must also be non-Abelian, meaning that exchanging particles in a different order will result in a different ground state of the overall system. The existence of such quasiparticles may seem counterintuitive, but evidence suggests they exist.
In addition to proving the existence of these non-Abelian anyons, one must work out how to control them to carry out the basic computing operations. This means being able to create the anyons as required, implement protocols to do particle exchange — two such exchanges are called a braid — and bring them back together to measure them.
One option is to use Majorana modes associated with the edge states of a topological superconductor. The most prominent implementation of this are one-dimensional semiconductor nanowires that become superconducting via the proximity effect, but claims that Majoranas have been observed in such devices are still controversial because trivial effects can mimic these zero-energy states. And, while some are confident that fabricating higher-quality materials will remove those trivial explanations1, reliably moving the Majoranas around to braid them is also still beyond our capabilities.
Three-dimensional topological superconductors will also feature Majorana modes on their edges and at the core of magnetic vortices. Candidate materials include UTe2 (ref. 2) and various iron-based superconductors3. However, these materials may also be unsuitable for practical implementation because it is not clear how to braid edge states of three-dimensional materials, and moving vortices around is difficult to scale to many qubits.
Enter the quantum Hall effect. This is one of the more abstract areas of condensed-matter physics, but on the positive side it is largely accepted that non-Abelian anyons exist in this setting4 and that they can be braided5 in interferometer devices like the one pictured6.
When a strong magnetic field is applied perpendicular to a two-dimensional system, the allowed energy states for the electrons or holes in that system are highly degenerate bands called Landau levels. When a Landau level is completely filled, current can only flow via the topological edge states (producing a transverse response) and the bulk of the sample is insulating, meaning that the longitudinal conductivity goes to zero. This is known as the integer quantum Hall effect.
When a Landau level is fractionally filled, a similar transport response can occur. This happens because electrons in the partially filled level can group themselves with the quanta of magnetic flux to create composite particles. This flux attachment mechanism gives states that fill the resulting Landau levels, providing an analogue of the integer filling. For example, when a level is one-third full of electrons, each electron can team up with three fluxes to account for all of the magnetic field and mimic a full level. The fractionalization of the electrons associated with these states indicates that the composite particles are anyons.
However, these composite anyons are merely Abelian and so are not helpful for topological quantum computation. But if these composite particles pair up with the correct symmetry of the combined wave function, it elevates their statistics to become non-Abelian. Among the various available theoretical proposals for how this can happen, one of the more straightforward is that the composite anyons pair with p-wave symmetry, a bit like a standard topological superconductor. This is predicted to happen when two-and-a-half Landau levels are filled, and experimental evidence looks promising that this is true4.
There are still many practical challenges associated with implementing a topological qubit from fractional quantum Hall anyons, as there are with all of the platforms we have discussed. In particular, the fractional states are rather fragile (although perhaps less so in graphene than in semiconductors7) and the degree of control needed to isolate and manipulate them will require exquisitely engineered devices. So, perhaps another platform might win the race to perform the first topologically protected quantum computations, but for now we would not bet against the dark horse of quantum Hall systems getting there first.