Data collection
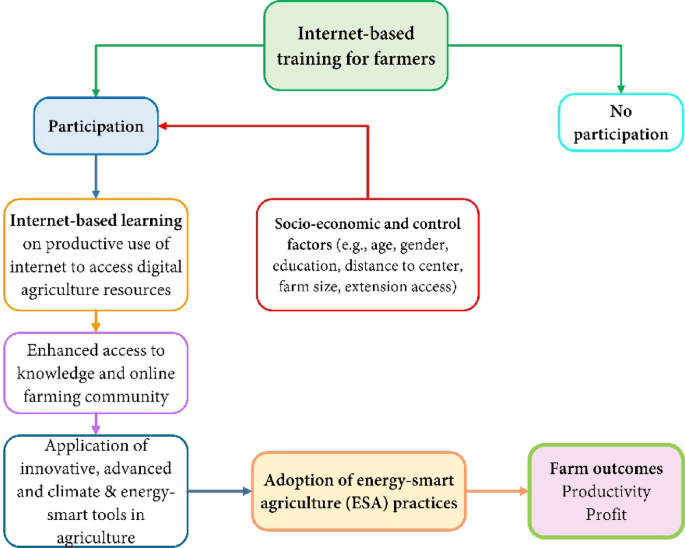
The study utilized cross-sectional data gathered from Okara and Pakpattan districts of Punjab through a well-structured questionnaire. To obtain a robust sample for consistent estimates of training participation, we followed a systematic process based on the training protocol, recruitment strategy, and participation rates. The Digital Dera used a blended learning approach, combining both face-to-face and online learning modules. These covered key topics such as soil analysis, market information access, weather forecasts, smart irrigation techniques, modern agricultural technologies, and certified seeds. Additional online modules were provided for follow-up learning. The recruitment strategy included several methods: advertisements in nearby input-output markets, local community outreach, and word-of-mouth through farmer networks. Local village-level leaders also played a significant role in recruiting farmers. In total, Digital Dera invited approximately 2,000 farmers in two phases, of which 1,357 farmers participated, resulting in a participation rate of 68%. The non-participation rate was mainly due to time constraints and geographical barriers. Of the participants, nearly 91% were from within a 19 km radius of the training center, which includes villages from both the Pakpattan and Okara districts. While the training was conducted in Pakpattan district, farmers from 9 Okara villages within this radius also took part in the program. These districts were chosen due to the presence of a Digital Dera in Pakpattan and their geographical proximity, ensuring equal opportunities for training participation in both districts.
The sample size for this study was calculated based on a population of approximately 25,000 registered landowner farmers across both districts, with a 95% confidence level (Z-value of 1.96), a margin of error of 5% (0.05), and a population proportion of 50% (0.5) to capture the maximum variability among farmers. Using the following formula (Eq. 1), we determined the required sample size to be 379 respondents.
$$n=\frac{{Z}^{2}.p.(1-p)}{({E}^{2}.\left(1-N\right)+({Z}^{2}.p.(1-p))}$$
(1)
However, recognizing that many small farmers are not registered as landowners or many farmers instead work on rented or leased land, we adjusted for this by doubling the sample size to ensure a more representative and robust sample. This resulted in a final sample of 723 completed questionnaires which is almost double of the statistically suggested sample size of 379. To collect data from households, a multi-stage random sampling technique was employed. This method offers significant statistical rigor and practical flexibility, making it ideal for a field survey that includes both participants and non-participants from large populations. First, stratified random sampling was used to select the Okara and Pakpattan districts to ensure diversity in the farmers’ decisions to participate. Next, random assignment was used to select both the control and treatment groups. For the treatment group, 400 farmers based on training participants information obtained from Digital Dera (approximately 33%) were randomly selected. It covers farmers from 18 villages (13 in Pakpattan and 5 in Okara) who had participated in successful training sessions, yielding 314 usable responses. In the control group, 409 non-participants were selected from the same districts, but with a minimum distance of 25 km from the training sites (which had a 19 km radius for participants). This distance was maintained to avoid potential biases and to ensure the representativeness of the sample by capturing socio-economically similar farmers with different access to training resources. The final sample consisted of 57% (409) control group and 43% (314) treatment group households. Table 1 presents a summary of the socio-demographic characteristics of the respondents and key study variables, including five ESA practices and various outcome and control variables used for further analysis.
The final field survey for data collection was conducted between December and February of 2024. Before conducting the field survey, a team of local enumerators, consisting of individuals with a Master’s degree (7) and PhD (5) students, underwent training to conduct a pilot survey to identify weaknesses and loopholes in the questionnaire. The study questionnaire and research methods adhered to relevant guidelines and regulations and were approved by the ethics committee of Institute of Agricultural and Resource Economics, University of Agriculture Faisalabad, Pakistan. For the final field survey, the questionnaire was translated into Urdu, and enumerators were also trained to conduct interviews in Punjabi when necessary. Prior to conducting the survey, we clearly explained its purpose and content to all participants. The study ensured complete anonymity, with no personal data collected beyond survey responses. Following standard research practices in Pakistan for such anonymous studies, we obtained verbal and written informed consent from all participants. To minimize bias, we incorporated various control variables, treatment variables, and reverse response-based questions. Notably, our sampling strategy and the design of the questionnaire – including control and treatment variables – help mitigate bias, as confirmed by the validity measures in the results. The finalized questionnaire was comprehensive and well-organized. It covers variables such as farm characteristics, demographics, farmers’ education, information sources, control variables, and digital training. In addition, information on other socioeconomic variables was included.
Variable selectionControl variables
Previous studies has explored the determinants of climate-smart technology adoption44,45, sustainable agriculture46,47, and technology adoption48,49. Building on previous studies and field surveys, particularly focus group discussions, this study incorporates relevant control variables to examine farmers’ access to digital training. Specifically, it includes demographic variables such as farmers’ age, gender, education, and marital status, as well as socioeconomic factors like farm size, farming experience, livestock holdings, smartphone ownership, and social circle. Additionally, institutional variables such as membership in farmer-based organizations (FBOs), access to farm advisory services, and access to credit are considered.
Demographic variables are used to assess the influence of personal characteristics on farmers’ participation in digital training, while socioeconomic variables account for differences in farm size, wealth, and access to information. Institutional variables measure the impact of organizational and institutional factors on participation and their corresponding effects on farmers. Moreover, farming system variables, including wheat-rice and mixed cropping systems, are integrated into the analysis to provide a comprehensive understanding of the factors influencing digital training participation.
Treatment variables
This study used five treatment variables: fines and inspection, access to subsidized technology, access to skill development training, access to markets for selling crop residues, and simultaneous access to both training and subsidized technology. Farmers without access to either technology or skill development services were designated as the control group. Each treatment was represented by dummy variables, where a value of 1 indicated access and 0 indicated no access. A detailed description of the treatment variables is provided in Table 1.
Instrumental variables
In this study, we employed three instrumental variables (IVs) to address potential endogeneity: (1) access to internet connection, (2) distance to Digital Dera, and (3) farm radius. Each of these IVs is directly related to participation in digital training but is not associated with the adoption of ESA practices and other outcome variables.
The first IV is access to internet connection, which can influence a farmer’s participation in digital training, particularly as some training modules require self-learning at home. Farmers with internet access are more likely to participate in the training. However, access to the internet does not have a direct impact on the adoption of ESA practices or farm productivity. The second IV is distance to Digital Dera. A shorter distance to the training center increases the likelihood of participating in the digital training. Therefore, the distance to the training center is positively related to participation but does not have a direct impact on the dependent variables – adoption of ESA practices, farm productivity, or net farm returns. Similar studies have used distance, such as distance to extension services or advisory offices, as an instrumental variable50,51. The third IV is farm radius, which refers to the number of training participants within a 3 km radius of a farmer’s location. A higher number of nearby training participants can encourage participation through word-of-mouth or the sharing of information. However, farm radius is exogenous to the dependent variables and does not directly influence the adoption of ESA practices or farm productivity. A similar study52 used farm radius as an instrumental variable in a comparable context.
Thus, these three IVs satisfy the exclusion restriction, validity (exogeneity), and relevance criteria, as they are not directly related to the dependent variables but are significantly associated with the endogenous explanatory variables.
Outcome variables
The primary outcome variables in this study are the adoption of ESA practices, farm productivity, and net farm returns. ESA practices are measured by whether a farmer adopts Direct Seeded Rice (DSR), Crop Residue Management (CRM), Zero Tillage (ZT), Legume Intercropping (LI), and Precision Water Management (PWM). Farm productivity is assessed by calculating the average per acre yield of rice and wheat. Similarly, the outcome variable for net farm returns is determined by subtracting variable costs from annual farm revenue per acre. Importantly, net farm returns also include income generated from the sale of crop residues of wheat and rice, as a market for crop residues exists in the study districts.
Table 1 Description of the study Variables.Modelling the impacts of digital training participation
We employed an endogenous switching regression (ESR) model to analyze the factors influencing digital training participation, productivity, and net farm return. ESR was chosen for its robustness in addressing endogeneity, a critical issue when evaluating the impacts of agricultural programs. Endogeneity occurs when unobservable factors affect both participation and outcomes, which can lead to biased results when using ordinary least squares (OLS) regression. Unlike experimental data from randomized control trials, cross-sectional surveys lack counterfactual information, making it more difficult to draw causal conclusions.
In our case, the ESR framework offers several advantages over the standard two-stage least squares (2SLS) approach. First, it has greater power in handling treatment effect heterogeneity, as some farmers participated in the training while others did not. Second, ESR is better at accounting for sample selection bias, a potential issue in our study using the 2SLS approach. Since ESR explicitly addresses sample selection, it provides more robust estimates in our scenario. Third, unlike the standard 2SLS approach, ESR uses a unified mechanism to simultaneously handle both treated and control groups. Additionally, since our study sample consists of only two districts, issues with random assignment of treatment could lead to endogeneity and inconsistent estimations due to observed and unobserved factors influencing farmers’ training participation. In this context, the ESR framework is more effective, as it estimates both outcome equations simultaneously, leading to more reliable results.
The study from53 propose analyzing the direct effect of participation by comparing outcomes among farm households. Since farmers make a choice to participate or abstain, the observed outcome variables can take the given expression:
$${Y}_{i}^{0}={X}_{i}{\beta }_{0}+{{\upepsilon }}_{0} (Non-participants)$$
(2)
$${Y}_{i}^{1}={X}_{i}{\beta }_{1}+{{\upepsilon }}_{1} \left(Participants\right)$$
(3)
Equations 2 and 3 model the conditional potential outcomes of internet-based training participation on farm performance. Here: first \({Y}_{i}^{0}\) compute outcomes variable under non-participation, and \({Y}_{i}^{1}\) denotes the outcome under participation, xi captures observed covariates (e.g., farmer education, age, input access), and\({{\upepsilon }}_{i}\) is the error term accounting for unobserved factors. Given this, we can model farmers’ choice for participation in internet-based training (selection equation) as:
$${D}_{i}^{*}={\text{Z}}_{i}\gamma +{\mu }_{i} with {D}_{i}\left\{\left.\begin{array}{c}1, if {D}_{i}^{*}>0\\ 0, Otherwise\end{array}\right\}\right.$$
(4)
Equation 4 specifies a selection model that governs farmers’ decisions to participate in training programs. This model assumes the error terms follow a multivariate normal distribution with zero mean and covariance. This framework corrects for selection bias arising from unobserved confounders (e.g., intrinsic motivation) that correlate with both participation decisions and outcomes.
Given this, we can model outcome equations:
$$E\left[{Y}_{i}^{0}∣{D}_{i}=0\right]={X}_{i}{\beta }_{0}+{{\upsigma }}_{0}{{\uplambda }}_{0}; E\left[{Y}_{i}^{1}∣{D}_{i}=1\right]={X}_{i}{\beta }_{1}+{{\upsigma }}_{1}{{\uplambda }}_{1}$$
(5)
In Eq. 5, we introduced inverse Mills ratio terms (λ0, λ1) correct selection bias. Average treatment effect on treated (ATT) can be expressed as follows:
$$ATT=\left[{Y}_{i}^{1}∣{D}_{i}=1\right]-E\left[{Y}_{i}^{0}∣{D}_{i}=1\right]={\left({X}_{i}{\beta }_{1}+{{\upsigma }}_{1}{{\uplambda }}_{1}\right)-(X}_{i}{\beta }_{0}+{{\upsigma }}_{0}{{\uplambda }}_{0})$$
(6)
Equation 6 estimates the overall impact of internet-based training participation on outcomes (e.g., productivity, and net farm returns). Using ESR, we can use control function approach to correct endogeneity:
$${W}_{i}={Z}_{i}\pi +{\eta }_{i} \left(\text{f}\text{i}\text{r}\text{s}\text{t} \text{s}\text{t}\text{a}\text{g}\text{e}\right)$$
(7)
$${Y}_{ij}={X}_{i}\beta +{{\theta }_{i}\widehat{\eta }}_{i}+{ \epsilon }_{i} \left(\text{s}\text{e}\text{c}\text{o}\text{n}\text{d} \text{s}\text{t}\text{a}\text{g}\text{e}\right)$$
(8)
Equations 7 and 8 helps correct the potential endogeneity of key covariates (e.g., access to farm advisory, off-farm income, internet use).
Sensitivity analysis
We conducted a sensitivity analysis to further validate the results obtained from the ESR model. In this process, we utilized boxplots, as they are more appropriate for studies involving PSM and robustness checks. Compared to line charts, boxplots are better suited for illustrating data variability and effectively represent how outcome variables differ within and across treatment groups.
Robustness checks
In the first stage, we tested the relationship between the instruments and the exogenous regressor using the multivariate Cragg-Donald Wald F-test to address the weak instrument assumption. Additionally, we conducted the Hansen J statistic test for IV models, which evaluates the null hypothesis that all instruments are valid (i.e., the over-identification test). The Hansen J statistic is especially useful in the ESR approach for assessing the validity of the instruments.
Furthermore, we applied the Durbin-Wu-Hausman chi-square test and the Wu-Hausman test to examine the endogeneity, strength, and consistency of the instruments. We also used the Anderson canonical correlation LM statistic to assess potential under-identification of the instruments (relevance). To check for multicollinearity, we tested the variance inflation factor (VIF), and the Breusch-Pagan test statistic was used to investigate the presence of heteroscedasticity, which is a common issue in cross-sectional data. These tests were performed to address endogeneity and self-selection bias, and we proceeded with our ESR estimations by inflating the asymptotic variance of the estimators used.