A hotter sample of water may freeze faster, than a colder one, when kept inside a refrigerator working at a subfreezing temperature1,2,3,4,5. This counterintuitive fact is now referred to as the Mpemba Effect (ME)6 and discussed since the time of Aristotle7. In recent times, in efforts to generalize the effect, several other experimental systems and theoretical models8,9,10,11 were shown to exhibit similar phenomena. Examples include cooling granular gases12,13, clathrate hydrates14, anti-ferromagnets15, spin glasses16, quantum systems17,18,19, driven binary mixtures20, Yukawa fluids21, as well as, perhaps even more surprisingly, pure ferromagnetic systems3,22,23. Despite the continuously growing list of such systems, the ME remains still a puzzle. There exists no clear hint whether a common fact is responsible for the observations in different systems. In fact, for the original system, i.e., water, even a demonstration via computer simulations is nonexistent, though there are works by providing possible explanations if the effect indeed exists1,2,24,25,26,27,28. Such a status is perhaps due to the difficulty owing to the complex natures of water molecules and related interactions29 that do not allow simulations of adequately large systems for long enough times. The long simulations are needed to counter the metastable features that may severely delay nucleation for a transition from a fluid phase to ice.
An important question here is to ask: How the ME may be connected to the above stated metastability – Should the longevity of the latter be a function of the initial temperature? Or, growth, following the nucleation, is the only contributor to the initial temperature dependence of the transformation? Questions have also been raised if the ME is a result of differences in times for reaching the final temperature, Tf, from different starting temperatures, Ts24,30. To address these issues, and obtain a more general picture, in addition to theoretical and computational studies of water, it should also be of interest to undertake studies of simpler systems exhibiting fluid to solid transitions. Here, we study such transitions in a model water31 and a simpler Lennard-Jones (LJ) system32, without impurities. In each of the considered cases, we prepare equilibrium fluid configurations at different Ts. These configurations are quenched to a fixed Tf, at which the thermodynamic phase is a solid one.
For the LJ systems, in space dimension d = 2, we perform molecular dynamics (MD) simulations32,33 using a truncated, shifted, and force-corrected potential, within which two particles at a distance r apart interact via32,34
$$u(r)=U(r)-U({r}_{c})-(r-{r}_{c}){\left.\frac{dU}{dr}\right| }_{r = {r}_{c}},$$
(1)
with \(U(r)=4\varepsilon \left[{(\sigma /r)}^{12}-{(\sigma /r)}^{6}\right],\) the standard LJ potential. Here rc is a cut-off distance, σ is the particle diameter and ε is the strength of the interaction.
For the simulations of water, we have chosen a rather realistic model31: TIP4P/Ice. This is a four-point rigid water model with transferable intermolecular potential. There, in addition to the points related to the positions of one oxygen (O) atom and two hydrogen (H) atoms, an additional point exists. This point, having a (negative) charge 1.1794, in electronic unit, is placed at a fixed distance (0.1577 Å) from O along the bisector of the H-O-H angle, having experimental value31104.52∘. The O atoms interact with each other via the standard LJ potential, with ε = 0.21084 kcal/mole. Each H-atom carries a positive charge of magnitude 0.5897. All charge points, expectedly, interact via the Coulombic potential (incorporated appropriately by avoiding overlapping feature)31V ∝ 1/r, the constant of proportionality being provided by charges and medium property. The masses of O and H atoms are set to be 15.9994 amu and 1.008 amu, respectively. Below we discuss a few of the above cited computational works on water, that used models different from the one considered by us.
Jin and Goddard25, from the analysis of density of states in a certain range of frequency, suggest that the presence of ME may be attributed to the higher population of hexamer states at elevated temperature. In a work by Tao et al.28, densities of (hydrogen) bonds of various types were calculated at different temperatures. They explain ME from the observed dependence of the densities, of bonds of effective electrostatic and covalent characters, on temperature. In ref. 27 several models of water were studied with significantly large number of molecules. Instead of carrying out quenching experiments, objective of these authors was to test the idea of Torrente et al.35 that breaking of equipartition during the relaxation process can generate ME in water, like in granular gases. Though these works are important for the understanding of ME, the effect was not demonstrated in any of these. We, for that purpose, have chosen a suitable model and devised an appropriate working strategy.
It should be noted that different models of water provide varying accuracy for (experimentally estimated) features like ice polymorphs, phase coexistence, melting point and temperature of maximum density. E.g., TIP5P36 estimates the melting point quite well, viz., 274 K at 1 bar. On the other hand, TIP4P37 estimates the overall phase diagram better than TIP3P37, or even TIP5P38. Interestingly, for TIP5P hexagonal ice is not the stable phase at normal melting point, unlike the TIP4P/Ice case which also estimates the melting point with good accuracy31. It should be noted that TIP4P/Ice31 is a re-parametrization of other versions of TIP4P37,38, which already were well suited for the phase diagram and ice properties, to improve the melting temperature of hexagonal ice. Thus, for our work, we have chosen TIP4P/Ice. For water, achieving ice nucleation under (unseeded) homogeneous condition is a difficult task, as described above39,40. For our chosen model31,41 this occurs, (presumably) due to somewhat lower nucleation barrier, though at temperatures much lower than the melting temperature, say, ≲ 40K. This was already shown for the original TIP4P model39. It is also computationally more suitable, compared to the next higher point model, because of the fact that for various TIP`N’P models CPU time significantly increases with the increase in the number of points (N).
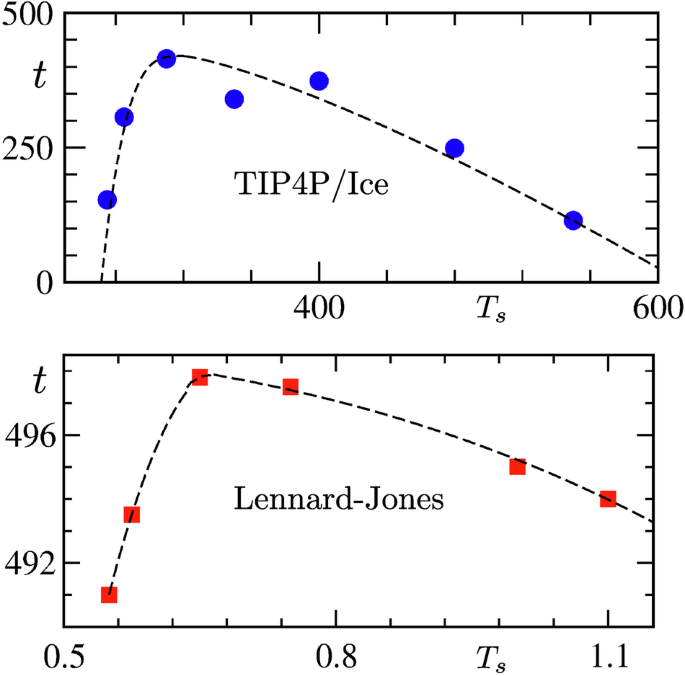
It may be appreciated that higher possibility of fluctuations should enhance the scope of nucleation. Consideration of small systems may severely restrict such chances. On the other hand, handling large systems is a difficult task, when the requirement is to simulate for long times that may be a necessity for the present problem for a certain range of Ts. Thus, it is important to adopt a “trade-off” between system size and run length3. Following this strategy, along with the clever choice of model, we have been able to realize ice formation, starting with pure fluid configurations, for a large range of Ts. From the analysis of the corresponding data sets we find clear evidence of ME in this as well as in the LJ model. For water, our results demonstrate that delay in nucleation, due to metastability, alone can exhibit ME-like feature, apart from the post nucleation growth part. In the case of LJ model, metastability is not a matter of concern, for reasons that we discuss later.
Results from the LJ model and water provide an interesting classification of ME based on the role of metastability. We also present results for para-to-ferromagnetic transitions in Potts model22,23,42, Hamiltonian of which, \(H=-J{\sum }_{ \ }{\delta }_{{S}_{i},{S}_{j}}\), provides critical temperature42\({T}_{c}=J/[{k}_{B}\ln (1+\sqrt{q})]\), with J ( = 1) being the interaction strength, kB the Boltzmann constant and q the number of possible states for a spin Si sitting at a lattice site i. This is to further substantiate the conclusion from the LJ case that ME can be observed in absence of metastability as well3,22,43, driven, for example, by the differences in critical fluctuations at various starting points3,22,23. Such critical-fluctuation induced ME should occur in the case of water as well. The present work opens up this and other possibilities that we will discuss later.
We have studied Mpemba effect in the TIP4P/Ice and the LJ models. For this purpose, initial configurations were prepared at various temperatures belonging to the respective fluid phases. These were quenched to temperatures at which the thermodynamically stable phases are solid ones. In both the cases we observe that configurations at higher temperatures, following the quenches, solidify earlier. However, the reasons in the two cases appear different. As opposed to the fact of metastability in the case of Ice formation, the Mpemba effect in the LJ model is driven by differences in critical fluctuations in the initial states. The latter is in line with our observations in the case of Potts model.