First, we study the quantum dynamics of EP transport an “ideal” organic microcavity model without static disorder (cf. Fig. 1a). The cavity and molecular parameters are chosen to closely resemble the Rhodamine microcavity model of ref. 17, albeit with a simpler vibrational structure: in each molecule, a vibrational mode couples to the electronic transition which is parameterized by the vibronic coupling constant κ. Details of the model are given in “Methods”.
Fig. 1: Overview of exciton-polariton transport model.
a Schematic of an organic microcavity filled with an ordered molecular ensemble in which all molecular TDMs \({\overrightarrow{\mu }}_{01}\) are aligned with the cavity polarization direction. b Static and dynamic disorder are included in the model by sampling the molecular electronic excitation energies \({\omega }_{m}^{\,{j}}\) from a Gaussian distribution P(ω), and by introducing vibronic coupling (characterized by κ), respectively. The latter results in nuclear motion in the excited electronic state. c Polariton dispersion curve ωLP/UP(kx) with bare molecular ωm and bare cavity ωcav dispersion. d Corresponding exciton content and e group velocities of lower and upper polariton branches. Colored circles in (c–e) mark the polaritonic states targeted through resonant excitation by an external laser pulse.
Due to their hybrid light-matter nature, EPs can propagate along the in-plane direction of the cavity with group velocity \({v}_{{{\rm{gr}}}}^{{{\rm{LP/UP}}}}=\partial {\omega }_{{{\rm{LP/UP}}}}/\partial {k}_{x}\), where ωLP/UP denotes the dispersion relation of the upper polariton branch (UPB) and lower polariton branch (LPB). The polariton dispersion, group velocity, and exciton content in the absence of vibronic coupling are shown in Fig. 1c–e, and play a vital role in our analysis.
Experimentally, EP transport is initiated either via off-resonant13,15,16 or resonant excitation12,14,20,34. In the first case, a focused laser pulse pumps the transition to a high-lying electronic excited state from where the system relaxes incoherently to the S1 state. In our simulations, off-resonant excitation is modeled by instantly promoting a single molecule to the S1 state while all other constituents of the system remain in their respective ground state17. In the second case, incidence angle and frequency of the laser pulse target a specific point on the polaritonic dispersion curve, coherently exciting a polaritonic wavepacket centered around a well-defined in-plane momentum \({k}_{x}^{(0)}\) and energy ℏωL. All relevant model and laser parameters are summarized in Table 1.
Table 1 Cavity (ω0, n, τcav, ℏΩR), molecular (ωm, \({\bar{\omega }}_{m}\), σm, ωvib, κ, Δx), and laser parameters (Ft, Fx, t0, x0) relevant to simulations
After excitation, we trace the spatiotemporal polariton dynamics by computing the real-time and real-space resolved polaritonic density ∣ψpol(xj, t)∣2 and the individual contributions from the photonic (∣ψphot(xj, t)∣2) and molecular (∣ψmol(xj, t)∣2) subsystems, as well as the momentum-resolved photonic density ∣ψphot(kx,p, t)∣2. These quantities can be readily leveraged from the propagated ML-MCTDH wavefunction by projecting onto localized photonic and molecular excitations, or onto photonic momentum-eigenstates17.
Off-resonant excitation
Sudden localized excitation of a single molecule in real-space creates a delocalized excitation in energy-momentum space, affording a superposition of a broad range of LPB and UPB polaritons. Consequently, components with a broad range of group velocities propagate away from the initial off-resonant excitation spot at x0 = 2.5 μm.
Without vibronic coupling (κ = 0), (Fig. 2a, upper panel), a wavefront moving linearly at the maximum LP group velocity \({v}_{{{\rm{gr}}}}^{{{\rm{LP}}},\max }=67.9\) μm ps−1 is visible in the polaritonic as well as photonic and molecular densities, while zooming in on the photonic real-space density reveals the presence of an additional—but faint—wavefront at the maximum UP group velocity which is close to the speed of light (\({v}_{{{\rm{gr}}}}^{{{\rm{UP}}},\max }=235\) μm ps−1).
Fig. 2: Impact of vibronic coupling on EP transport after off-resonant excitation.
a Real-space resolved total polaritonic density ∣ψpol(x, t)∣2 = ∣ψmol(x, t)∣2 + ∣ψphot(x, t)∣2, molecular and photonic contributions ∣ψmol(x, t)∣2 and ∣ψphot(x, t)∣2, respectively, for vibronic coupling strengths κ = 0, 50, 80 meV. Cyan and orange dashed lines indicate linear motion at the maximum group velocities of LPB (67.9 μm ps−1) and UPB (235 μm ps−1), respectively. Red lines trace the expectation value of the position operator. b Time-dependent population of excited cavity modes (“cav”) and molecular excitons (“mol”). c MSDs extracted from real-space resolved densities in (a). d Expectation value of cavity mode in-plane momentum for propagating EPs in (a). e Initial and final momentum distribution for κ = 80 meV and various detuning Δexc of molecular electronic excitation energy with respect to cavity photon energy ω0. The corresponding resonant wavevector \({k}_{x}^{{{\rm{res}}}}\) is indicated by a black vertical line. All distributions in (e) have been normalized.
As such, when vibrations do not couple to the electronic transition, transport after off-resonant excitation is driven mainly by the photonic part of the wavefunction: in Fig. 2a, c mean position and mean square displacement (MSD) of the photonic subsystem exceed those of the molecular subsystem significantly, and a large part of the molecular density remains at the initial excitation spot.
This can be explained by the fact that the initial single-molecule excited state has largest overlap with polaritonic states with high molecular contribution, which are located on the far right of the LPB dispersion, and the far left of the UPB dispersion curve (cf. Fig. 1d). Thus, the initial molecular excitation mostly spans polaritonic states with vanishing group velocity, as can be seen from Fig. 1e. Fast moving components close to the speed of light originate from high in-plane momentum UPB states which have negligible excitonic contribution (Fig. 1d, e). Therefore, their signatures are weak and only visible in the photonic density.
The presence of dynamic disorder due to non-zero vibronic coupling κ drastically changes the polariton transport dynamics: increasing κ in Fig. 2a shifts formerly stationary or slowly propagating components toward the wavefront, which moves at \({v}_{{{\rm{gr}}}}^{{{\rm{LP}}},\max }\). This enhances the mobility substantially, as indicated by the mean polaritonic position and MSD in Fig. 2a, c. Furthermore, the mobility-enhancement occurs dynamically, i.e., the mean group velocity increases over time, which can be seen from the increasing slope of time-dependent mean position 〈xpol〉(t) in Fig. 2a. The enhancement is more pronounced in the material subsystem, pointing at a vibronically-mediated mechanism that dynamically increases the mobility of exciton-like polaritons.
This mechanism demands closer analysis. Inspecting the total population of cavity modes and molecular excitonic states in Fig. 2b reveals an increasing photonic content over time for non-zero κ. For the largest vibronic coupling strength (κ = 80 meV), the light-matter composition changes from purely excitonic at the beginning of the simulation to a roughly 60/40 photonic/excitonic composition after approximately 100 fs. Moreover, the mean in-plane momentum of cavity modes in Fig. 2d stagnates around 8 μm−1 for κ = 0 meV but decreases noticeably to approximately 6 μm−1 for κ = 80 meV. These findings suggest vibration-driven relaxation on the LPB as the underlying mechanism for the mobility-enhancement, whereby population from highly excitonic, near-stationary states is transferred toward more photonic states with large group velocity (cf. Fig. 1d).
For κ ≠ 0, the initial wavepacket formed by off-resonant excitation, no longer corresponds to a superposition of excitonic-photonic eigenstates. Instead, intramolecular vibrations couple states on UPB and LPB, inducing VAS and RP processes. VAS and RP have been amply discussed for organic microcavity EPs21,22,23,26,35,36, and are relevant for polariton condensation5,37. Highly excitonic polaritonic states with large in-plane momentum on the LPB can scatter into a lower-momentum region with increased photonic character and increased group velocity, resulting in a dynamically increasing mean velocity as indicated by the change in the slope of the red line in Fig. 2a. Scattering processes on the UPB, on the other hand, do marginally contribute to this transport-enhancement since fast-propagating, increasingly photonic states are located at high in-plane momenta and possess high energy, making them hardly accessible from the off-resonantly excited initial state. Apart from that, scattering from the UPB to the LPB can contribute, as we discuss in the next section.
For better understanding of the underlying relaxation process, we inspect the momentum-resolved photonic populations ∣ψphot(kx)∣2 at ti = 5 fs and tf = 240 fs for various detunings Δexc between the excitonic resonance and the fundamental cavity frequency ω0 = 3.81 eV. This tunes the in-plane momentum \({k}_{x}^{{{\rm{res}}}}\) at which cavity mode and exciton are resonant, from low to high in-plane momentum, cf. Fig. 2e. We find in all cases a clear decrease in population of momentum-states to the right of the resonant in-plane momentum, and an increase to the left. Accordingly, mainly states with \({k}_{x}\le {k}_{x}^{{{\rm{res}}}}\), occasionally referred to as “bottleneck” polaritons15,23, participate in the vibration-driven relaxation. Moreover, these states do not relax down to kx = 0 but rather accumulate in the intermediate region \(0 of the LPB where molecular contributions are still appreciable and group velocities are high (cf. Fig. 1d, e).
Further relaxation is hindered by the decreasing efficiency of exciton-mediated scattering when the photonic content of involved states becomes large11,23,35. This effect is known as the “phonon bottleneck” in the context of EP condensation5,18. Note that the wavevector-resolved photonic population cannot capture highly excitonic polaritons due to their vanishing photonic contribution. Nonetheless, the disappearing stationary component at x0 of ∣ψmol(x, t)∣2 for κ = 50 meV and κ = 80 meV in Fig. 2a indicates that they undergo relaxation on the LPB as well.
Resonant excitation
In the following, we investigate the relevance of molecular vibronic coupling in a wide range of resonant excitation scenarios targeting LPB and UPB. To this end, eight laser pulses are considered with pulse parameters (except photon energy and incidence angle, which are varied) given in Table 1. The resonantly targeted points in the [ω(kx), kx] plane are shown in Fig. 1c. First, we discuss two limiting cases on each branch: a highly photonic and a highly excitonic wavepacket, which, on the LPB, are found at small and large wavevectors, respectively. The situation inverts on the UPB, where the photonic content increases towards large wavevectors.
The LPB dispersion relation at small wavevectors is parabolic, such that coherently-excited wavepackets in this region display ballistic transport and dispersive behavior38. Our full-quantum dynamical results reproduce this for resonant excitation targeted at \({k}_{x}^{(0)}=2.75\) μm−1 (pulse 1) on the LPB, corresponding to an exciton content of 13.8% (cf. Fig. 1d). In Fig. 3a the mean position of the polaritonic density moves linearly, corresponding to quadratic growth of the MSD, while the width of the wavepacket spreads visibly during propagation in a lossless cavity. Polaritonic densities in both real and momentum space are identical for κ = 0 meV and κ = 80 meV (Fig. 3a, c); the wavevector-resolved cavity-mode population stays constant after the pulse, showing no signatures of relaxation (Fig. 3c). As discussed for the off-resonant case, the efficiency of vibration-mediated scattering processes decreases significantly towards the small-wavevector region on the LPB due to increasing photonic content. Consequently, the ballistic dispersive transport is unaffected by vibronic coupling in this regime.
Fig. 3: Transport enhancement through vibronically-mediated relaxation of resonantly excited EP wavepackets.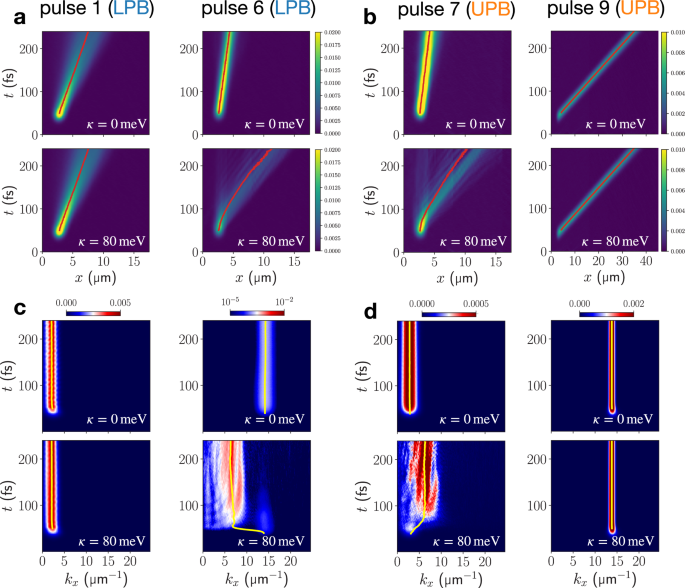
a Real-space resolved total polaritonic density ∣ψpol(x, t)∣2 for resonant-excitation to the LPB by pulse 1 and 6, at vibronic coupling strengths κ = 0 meV and κ = 80 meV. b Same as (a) but targeting the UPB by pulses 7 and 9. Red lines indicate the expectation value of the position operator. The momentum-resolved cavity mode populations corresponding to (a) and (b) are shown in (c) and (d), respectively. Yellow lines indicate the expectation value of the cavity-mode momentum operator.
Strong differences are found when the laser pulse addresses the highly excitonic region on the LPB, exciting at \({k}_{x}^{(0)}=14.5\) μm−1 (pulse 6) corresponding to an exciton content of ~90%. For κ = 0 meV transport proceeds ballistically, Fig. 3a, at low group velocity, but dispersion during propagation is less pronounced due to the non-parabolic, flat LPB dispersion relation in the large in-plane momentum region. Vibronic coupling significantly changes this behavior. Again, strong vibronic transport-enhancement becomes apparent from the polaritonic real-space density and mean position in Fig. 3a. Wavevector-resolved cavity populations in Fig. 3c reveals rapid relaxation of high in-plane momentum components of the LPB wavepacket to faster-propagating polaritons close to the “bottleneck region” below \({k}_{x}^{{{\rm{res}}}}=8.64\) μm−1 as the origin of the enhancement. These findings verify the participation of highly-excitonic LPB states in the vibration-mediated relaxation as discussed for off-resonantly excited polaritons.
Targeting the corresponding UPB states with pulses 7 and 9 results in an inverted situation: Now, excitation at large wavevectors affords a highly photonic EP wavepacket with large group velocity which is shielded from molecular vibronic effects through its low exciton content of ~7%. Consequently, we find ballistic transport independent of the vibronic coupling strength in Fig. 3b. In contrast, low-wavevector (pulse 7) excitation creates a predominantly excitonic EP wavepacket with low group velocity. Again, vibronic coupling results in relaxation of the wavepacket on the UPB to the “bottleneck region” in Fig. 3d which follows a similar fate as the LPB wavepacket excited by pulse 6 in Fig. 3c. As a result, the propagation velocity is significantly enhanced, producing very similar trajectories for initially highly excitonic wavepackets on the LPB and UPB (pulse 6 in Fig. 3a and pulse 9 in Fig. 3b). This suggests that vibronic interactions within molecules can efficiently funnel population towards the high-mobility region on the LPB close to \({k}_{x}^{{{\rm{res}}}}\) from both UP and LP states.
Next, we target the high-mobility region directly by excitation to the UPB and LPB at the resonant wavevector \({k}_{x}^{{{\rm{res}}}}\) (pulses 3 and 8 in Fig. 1c). Although possessing the same nominal group velocity and equal light-matter composition in the absence of vibronic coupling, UP and LP states at \({k}_{x}^{{{\rm{res}}}}\) undergo distinct relaxation dynamics, both resulting in a slow-down of polariton propagation when vibronic coupling is included, as seen in Fig. 4c. This is in stark contrast to the previously discussed highly excitonic UP and LP states which both follow similar relaxation pathways and exhibit vibronically-enhanced transport.
Fig. 4: EP propagation ensuing excitation at resonant wavevector.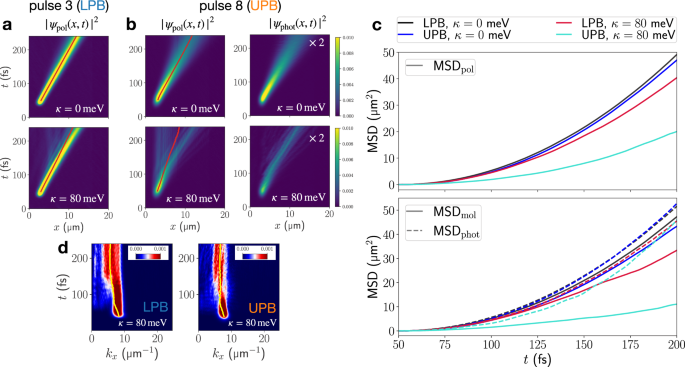
a Real-space resolved total polaritonic density ∣ψpol(x, t)∣2 for resonant-wavevector excitation to the LPB. b Real-space resolved total polaritonic density ∣ψpol(x, t)∣2 and photonic contribution ∣ψphot(x, t)∣2 for resonant-wavevector excitation to the UPB. Red lines indicate the expectation value of the position operator. c MSDs extracted from polaritonic real-space resolved densities in (a) and (b). d Momentum-resolved cavity mode populations corresponding to EP propagations at κ = 80 meV in (a) and (b). Yellow lines indicate the expectation value of the cavity-mode momentum operator.
After UP excitation, vibronic coupling leads to the appearance of non-propagating “vertical” features which lack any contribution from the cavity modes (Fig. 4b). Still, a component propagating at the expected group velocity persists in the photonic and polaritonic real-space densities. This results in the onset of an apparent diffusive transport, as indicated by the linear growth of the polaritonic and molecular MSDs in Fig. 4c toward the end of the simulation.
We can attribute this apparent slow-down effect for UP excitation to non-radiative decay from the UPB towards the dark states driven by vibronic motion. Polariton dynamics around the resonant wavevector can be regarded in close analogy to that of many molecules electronically coupled to a single resonant cavity mode. In that case, vibronic interactions in molecules have been found to support fast and efficient decay to the dark-state manifold from the UP state39,40.
For LP excitation at \({k}_{x}^{{{\rm{res}}}}\), such vertical features are not visible in the polaritonic density (cf. Fig. 4a). Instead, fractions with lower group velocities depart from propagating wavefront over time, indicating population transfer to polaritonic states with lower group velocities. Accordingly, intraband relaxation on the LPB dominates the dynamics after LP excitation, which can be traced through the wavevector-resolved photonic density in Fig. 4d. While this mechanism generally enhances the transport as observed in this study for off-resonant and resonant excitation schemes, it can only access slower-propagating states when starting at the resonant wavevector, i.e., close to the maximum of the LPB group velocity (cf. Fig. 1e).
Summarizing, our fully quantum-dynamical simulations of EP dynamics in a lossless cavity show that vibronic motion can strongly impact polariton transport depending on the initially targeted state. Vibronic interactions provide relaxation channels along and among polaritonic branches and dark states for appreciable exciton content (≥ 20%) of the targeted EP state. Generally, fast-propagating states close to the polariton bottleneck can be accessed efficiently from exciton-like UPB and LPB states. This results in a vibronic-enhancement of EP transport. However, close to the inflection point of LPB and UPB trapping within the dark-state manifold and low group velocity EP states close to kx = 0 become possible, resulting in a slow-down of EP transport.
Impact of static disorder
Organic semiconductor materials typically display a high degree of structural and energetic disorder, resulting in inhomogeneous broadening of the excitonic resonance. Static disorder in general is known to have substantial impact on a variety of transport processes in organic materials, including charge and exciton transport in organic semiconductors as well as polariton transport41,42,43,44. Within our fully quantum-dynamical framework, we investigate how static disorder in conjunction with vibronic interactions, i.e., dynamical disorder, governs the behavior of EP transport.
We model static energetic disorder in an organic microcavity by considering a Gaussian distribution of molecular electronic excitation energies with standard deviation σm = 30 meV and mean value \({\bar{\omega }}_{m}=4.18\) eV (cf. Fig. 1b). The corresponding linewidth (FHWM) of the excitonic resonance of ≈ 70 meV is representative of organic materials used in strong-coupling experiments45,46. The results presented in Fig. 5 are averages over simulations performed with five disorder realizations.
Fig. 5: EP propagation in the presence of static energetic disorder.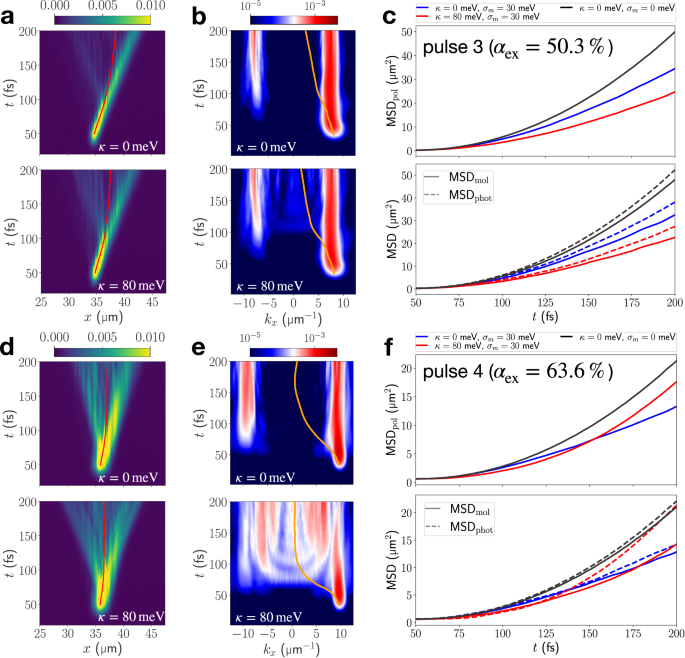
a Real-space resolved total polaritonic density ∣ψpol(x, t)∣2 for resonant-excitation to the LPB by pulse 3, at vibronic coupling strengths κ = 0 meV and κ = 80 meV and σm = 30 meV. Red lines indicate the expectation value of the position operator. b Momentum-resolved cavity mode populations corresponding to real-space densities in (a). Orange lines indicate the expectation value of the cavity-mode momentum operator. c MSDs extracted from polaritonic as well as molecular and photonic real-space resolved densities for resonant-excitation by pulse 3. d–f same as (a–c) but targeting the LPB by pulse 4. For pulse 4 an increased spatial FHWM (Fx = 1125 nm) is used to ensure that the resulting excitation in k-space stays within the momentum-range of the bidirectional cavity model.
In the presence of static disorder, the assumption of unidirectional transport can break down due to backscattering. In ref. 47 cavity modes with opposite in-plane momentum were found to participate strongly in the transport dynamics, and their inclusion was essential in accurately simulating EP mobility. We therefore modify the multimode cavity model to include negative in-plane momentum modes by choosing discretized kx,p = 2πp/Lx with \(p\in \left[-\frac{M}{2},\frac{M}{2}-1\right]\) and keeping the number of modes equal. The wavevectors of this bidirectional cavity model extend from approximately −12.5 to 12.5 μm−1.
Indeed, backscattering of the propagating polariton is a dominant process in all simulations presented in Fig. 5. This is clearly indicated by the polariton wavepacket spreading to the left and right in real-space (Fig. 5a, d), and the population of negative-momentum cavity modes within 20–50 fs after resonant excitation to positive-momentum region of the LPB (Fig. 5b, e). Over the course of the propagation, the photonic momentum-space densities evolve towards an approximately symmetric distribution (with respect to kx = 0), such that the average in-plane momentum 〈kx〉(t) tends to 0. As a result, the mean polariton position 〈xpol〉(t) approaches stationary behavior for longer propagation times (best visible in Fig. 5d), although a polaritonic wavepacket with positive kx is initially excited.
The (back)scattering processes induced by static energetic disorder within the molecules have a detrimental impact on polariton transport. Comparing the polaritonic MSDs for simulations with and without static disorder indicates suppressed transport in the disordered microcavity independent of the vibronic coupling strength (Fig. 5c, f). As discussed in refs. 22,44, inhomogeneous broadening of the exciton resonance increases scattering between the polariton and molecular excitations, thereby restricting the range of coherently propagating states on the LPB and increasing the number of incoherent, strongly localized states. This behavior, akin to Anderson localization41, is visible in Fig. 5a, d where stationary population builds up next to the propagating wavefront.
Without vibronic coupling, this leads to the onset of diffusive transport after a short ballistic phase, ca. 50 fs after the pulse as indicated by the change from quadratic to linear growth of the MSDs in Fig. 5c, f at 100–125 fs. Localization is more pronounced for pulse 4 since the impact of molecular disorder is increased due to the higher exciton content. In that case, polariton transport is most suppressed (Fig. 5f). These findings are in excellent agreement with previous studies on polariton transport in statically disordered systems in the absence of vibronic coupling47,48,49. Note that the previously proposed (static) disorder-enhanced transport regime44,49,50 is not observed here, since its onset occurs when the inhomogeneous broadening is comparable to the Rabi splitting47,50 whereas here σm /ΩR ≈ 10%.
When vibronic interactions are included (κ = 80 meV), transport behavior differs strongly for pulses 3 and 4. In the subsection “Resonant Excitation”, vibronic coupling has been found to result in a slow-down of EP transport after exciting to the LPB at the resonant wavevector with pulse 3. Vibronic effects hence amplify the static disorder effect for this excitation. Therefore, diffusive transport at a strongly reduced rate is observed in Fig. 5c.
In contrast, when targeting polaritons on the LPB with larger in-plane momenta, vibronic coupling has the opposite effect, enhancing transport by connecting slowly propagating exciton-like polaritons with the photon-like high-mobility region on the LPB (cf. pulse 6 in Fig. 3). This effect persists in the presence of static energetic disorder, as indicated by the emergent population of cavity modes in the bottleneck region around ± 6 μm−1 in Fig. 5e at 100 fs. Vibronic relaxation in combination with polariton backscattering results in a rapid “symmetrization” of the momentum-space populations, affording a relatively broad distribution with near-vanishing mean-momentum within ~50 fs after excitation.
Interestingly, this leads to a prolonged ballistic expansion phase with a larger final MSD compared to the disordered model without vibronic coupling (Fig. 5f): vibronic population transfer on the LPB accesses states which not only possess a higher intrinsic group velocity but are also less prone to scattering due to their increased photonic character. The molecular and photonic contributions to the MSD (Fig. 5f, lower panel) substantiate this, since enhancement is strongly linked to the photonic subsystem, whereas the molecular part propagates more slowly.
We note that none of these features are an artifact of averaging over only a small number of disorder realizations as all individual realizations display the same qualitative behavior (cf. Supplementary Fig. 5). Moreover, the main transport characteristics arising from the co-presence of vibronic coupling (“dynamic disorder”) and inhomogeneous broadening (“static disorder”) are closely related to EP transport in the presence of dynamical stochastic noise51. Both systems exhibit a ballistic-to-diffusive transition, symmetrization and broadening of the photonic k-space distribution, and an extended ballistic phase due to noise or vibronic coupling.
Impact of radiative decay
Finally, we introduce cavity losses to the cavity-molecule system since current FP cavity setups based on high-reflectivity metallic mirrors have radiative lifetimes of typically 10 fs to 30 fs due to cavity photon leakage to the electromagnetic continuum. This fundamentally limits the lifetime of polaritonic state, and thus has substantial impact on the transport properties of cavity-molecule systems. To single out the impact of radiative decay and its interplay with vibronic interactions, we employ the ideal crystal model without inhomogeneous broadening in the following.
We include spontaneous cavity losses in ML-MCTDH propagations through non-Hermitian damping terms \(-{\sum }_{{k}_{x}}{{\rm{i}}}\frac{{\Gamma }_{{k}_{x}}}{2}{\hat{a}}_{{k}_{x}}^{{\dagger} }{\hat{a}}_{{k}_{x}}\)29,52. A uniform decay constant ΓC = 1/τC is assumed for all cavity modes, with apparent cavity lifetime τC = 24 fs. As pointed out in earlier works, this ansatz is equivalent to propagating the density matrix according to a Lindblad master equation if the system stays within the electronic-photonic single-excitation subspace53,54. In our simulations, coupling strengths are sufficiently low and external pulses sufficiently short and weak such that this condition is met (Supplementary Fig. 3). When the norm of the polaritonic wavepacket has decreased below 1.5% of the initial laser-excited population, the wavepacket is considered to have decayed and MSDs are not computed beyond this point.
We compare the spatiotemporal evolution of five coherently excited LP wavepackets with increasing exciton content, tuning from the photonic (pulse 1) to the excitonic regime (pulse 6). While high photonic character of the initially excited polaritonic wavepacket protects transport against the impact of vibronic coupling, it makes EP transport highly vulnerable towards radiative decay in low-Q cavities. Since the emission rate is proportional to the photon number, the polaritonic density rapidly decays in a lossy cavity. This limits the observable transport to less than 100 fs after the pulse maximum, as seen in Fig. 6a, b.
Fig. 6: Impact of radiative decay on polariton transport.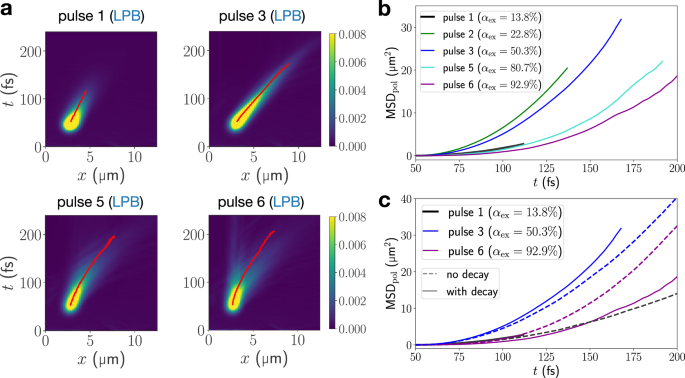
a Real-space resolved polaritonic densities ∣ψpol(x, t)∣2 for κ = 80 meV and three resonantly excited LPB wavepackets in a lossy cavity with τC = 24 fs. b MSD of propagating EP for a vibronic coupling strength of κ = 80 meV. EPs have been excited resonantly to five different points at the LPB by pulses 1–3,5,6; exciton contents αex at these targeted points are given in the legend. Red lines indicate the expectation value of the position operator. c Comparison of MSDs for pulses 1,3,6 in the presence and absence of radiative decay.
Moreover, our simulations in a lossy cavity indicate a significantly prolonged propagation when targeting the high in-plane momentum region of the LPB in Fig. 6b. Due to their excitonic nature, the impact of cavity losses on their lifetime is mitigated compared to the low-wavevector regime. Yet, vibronic interactions connect them to the more photonic bottleneck region of the LPB. Thus, exciton-like large-wavevector LP states can act as a reservoir from which population is fed to the fast-propagating polaritonic manifold. This leads to long-lived and efficient transport due to—not despite of—vibronic coupling. Our results are in line with a recent experiment12, which could support the exciton reservoir hypothesis26,55 as well.
In a lossy cavity, the interplay of vibronic effects with the varying group velocities and lifetimes along the EP dispersion curve creates distinct transport regimes on the LPB. The low-wavevector region (pulse 1) is characterized by low to moderate group velocities and rapid radiative decay, resulting in short-lived and short-distance polariton transport. Entering the bottleneck region (pulse 2), the group velocity has a maximum, but propagation duration is still strongly limited due to appreciable photonic content. Around the resonant wavevector (pulse 3), group velocities are still high and the increased excitonic content protects polaritons from cavity losses, enabling long-distance transport. Our simulations indicate that vibronic coupling has only minor impact on polariton motion in the regimes left of the resonant wavevector.
Remarkably, transport properties of lower-band polaritons to the right of the resonant wavevector (pulse 5) are improved in the presence of vibronic coupling by combining their long lifetimes and efficient access to the high-mobility bottleneck region of the LPB. This is illustrated by comparing polariton transport ensuing pulse 1 and pulse 5 (Fig. 6). Although both pulses target LPB states with very similar group velocities, the initially exciton-like wavepacket (pulse 5) propagates much longer and further than the quickly decaying photon-like wavepacket (pulse 1). When targeting even higher wavevectors, the vanishing photonic contribution and small group velocity begin to dominate (pulse 6). Overall, this affords an optimal transport regime on the LPB between exciton contents of approximately 50% and 80%. Initial photoexcitation to this region harnesses beneficial vibronic effects and favorable transport properties set by the polariton dispersion relation. As seen in Fig. 6b, LPB wavepackets with ~50% (pulse 3) and ~80% (pulse 5) exciton content display the longest propagation distances after 200 fs.