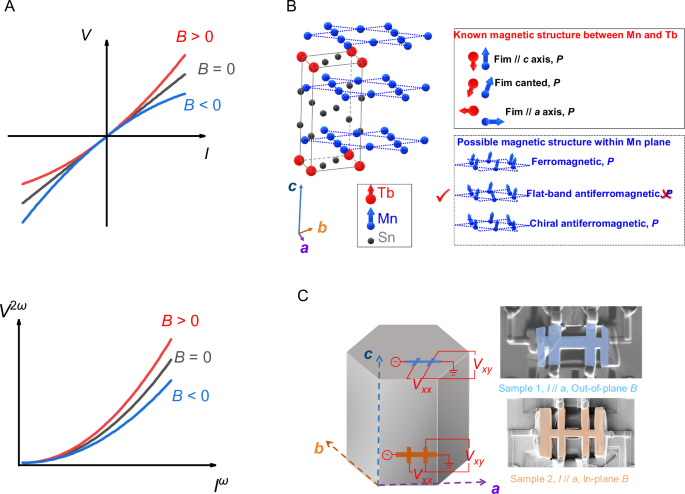
Modifying the crystal symmetry in a quantum material is one of the most important routes to manifesting sizeable DBC and Dmetric -induced nonlinear physics, such as that observed in artificially corrugated bilayer graphene20,21,22,23. An alternative approach in nonlinear responses is to introduce magnetic order to break symmetries. The kagome magnet system, such as the RMn6Sn6 family, where R is a rare earth element, is a promising candidate for locating this magnetism-induced symmetry-breaking behaviour. RMn6Sn6 compounds crystallize in a HfFe6Ge6-type structure (centrosymmetric space group P6/mmm), which possesses Mn kagome layers stacked along the c axis. In each unit cell, the R atoms occupy the honeycomb centres between two Mn layers. Except for the case of a nonmagnetic R (Y and Lu) atom, the competing magnetic interactions, namely direct Mn-Mn exchange, indirect 4f-3d type R-Mn exchange and Ruderman-Kittel-Kasuya-Yosida (RKKY) type R-R interactions, contribute to rather complicated magnetic structures, offering a rich field for nonlinear physics. Among these magnetic interactions, intralayer Mn-Mn interactions are the strongest, and therefore ferromagnetic coupling within the kagome planes dominates. The hybridization between Mn 3 d and R 5 d orbitals always favours antiparallel alignment, thus yielding a negative exchange coupling between Mn and R24. In RMn6Sn6, various magnetic structures have been observed, such as an easy-ab-plane anisotropy in GdMn6Sn6, an easy-c-axis anisotropy in TbMn6Sn6 and conical order in DyMn6Sn6 and HoMn6Sn625. Particularly, in TbMn6Sn6, the ferrimagnetic ordering forms below TC ~ 420 K, with both Tb and Mn magnetic moments aligned parallel/antiparallel to the a-axis, and, a spin reorientation18,19 occurs at TSR ~ 315 K, where the moments rotate into the c-axis with a slight canting angle, as shown in Fig. 1B, (more SR transition sketch and related magnetization measurements are available in Figures S1, S2). The canting effect is supported by magnetization measurements shown in Figure S2. The magnetization does not saturate at high magnetic field, and the in-plane and out-of-plane magnetic moments at B = 5 T at 300 K are different, e.g., 5.25 µB/f. u. and 5.19 µB/f. u., respectively. These results confirm the robust canted ferrimagnetic order and in-plane antiferromagnetic components at room temperature. The magnetic ordering in the kagome lattice contributes to large Berry curvature in the material, which leads to a giant anomalous Nernst effect26,27 and anomalous Hall effect25,28 at around room temperature16,19,25,26,27,29,30,31,32,33,34,35,36,37. On top of this, inelastic neutron scattering (INS) results16,17,19 indicate that the Mn in-plane spin configuration of the kagome lattice has magnetic excitation features of ferromagnetism, flat-band antiferromagnetism, and chiral antiferromagnetism (Fig. 1B). Importantly for this work, the flat-band type antiferromagnetic spin structure in the Mn kagome lattice, with an inversion-symmetric pair of Mn moments canting along opposite directions, result in breaking P and T, satisfying conditions to observe the quantum metric physics.
The anisotropic magnetotransport properties of TbMn6Sn6 with applied field along the c axis or the basal plane ([\(\bar{1}\bar{2}\)0] direction) for Sample 1 and Sample 2 (see Fig. 1C for sample orientation), respectively, have been studied (Figures S3, S4), indicating the excellent crystal quality of the studied devices. Figure 2A, B demonstrates the first-order transport results at 300 K. The negative magnetoresistance (MR) in Sample 1 is sharper at low fields, where the moments are not fully aligned, and shows linear dependency with fields above the alignment, indicating spin-disorder-scattering and electron-magnon scattering, respectively38. With applied in plane fields, a field-induced SR occurs, and shows a U-shape positive MR in the SR region, similar to the reports in the Fe3Sn2 kagome magnet39. A giant anomalous Hall effect arising from the large Berry curvature in the band structure27,28,37 is also observed in Samples 1 & 2, as shown in Fig. 2B. The anomalous Hall conductivity \({\sigma }_{{xy}}^{A}\) (=\(\,\frac{{\rho }_{{xy}}^{A}}{{\rho }_{{xy}}^{2}+{\rho }_{{xy}}^{2}}\)) is ~ 210 S·cm−1 in sample 1, which converts to ~ 0.122 e2/h (quantum conductance) per kagome plane, comparable with top-quality TbMn6Sn6 crystals in literature. In Sample 2, the similar result (0.13 e2/h) is also observed at room temperature, implying the Berry curvature may also contribute to an out-of-kagome plane giant anomalous Hall conductivity. The observed similar linear transport behavior in Sample 1 and Sample 2 also suggests that the electronic properties in TbMn6Sn6 are not affected by the FIB fabrication process. Similar behavior can be found in the 290–320 K region, as demonstrated in Figure S3; the calculated anomalous Hall conductivity values are summarized in Fig. 2G. The anomalous conductivity is roughly a constant, and independent with the longitudinal conductivity, also suggesting the intrinsic origin from the Berry curvature.
Fig. 2: The anisotropic transport properties of TbMn6Sn6 at 300 K.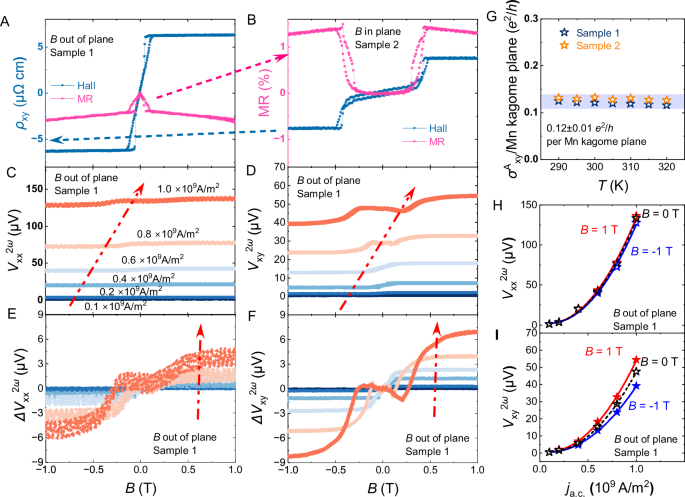
A, B The first order magnetotransport properties of Sample 1 and Sample 2 in −1 – 1 T range, in which the Hall effect of both samples are plotted in blue curves and use the blue y axis in Panel (A), the magnetoresistance (MR) curves are plotted in pink and share the purple y axis in Panel (B). C, D The nontrivial longitudinal (\({V}_{{xx}}^{2\omega }\)) and transverse (\({V}_{{xy}}^{2\omega }\)) second harmonic response in Sample 1 with different applied alternating current (a.c.) densities. E, F The magnetic-field (B) dependent components (\({{\Delta }V}_{{xx}}^{2\omega }\) and \({{\Delta }V}_{{xy}}^{2\omega }\)) in the nonlinear response shown in Panel C&D, respectively. Note that, Panel (C–F) share the same color code for current density level, which is labelled in Panel (C) and indicated by the red arrows along increasing current density directions in each Panel. G The Berry curvature induced anomalous Hall conductivity in 290–320 K temperature (T) region, which is converted to quantum conductance per Mn-kagome plane. The 0.12 ± 0.01 e2/h region is highlighted by light-blue shade. H The longitudinal and (I) transverse second-order responses (star symbols) at different magnetic fields are plotted against the applied a.c. density along the a axis, together with parabolic fitting curves.
A frequency doubling effect was observed in the FIB-fabricated Hall bar samples by the application of an alternating current (a.c.), as shown in Fig. 2C–F for Sample 1, and Figure S5 for Sample 2. Figure 2 C&D show both longitudinal and transverse second harmonic responses \({{\rm{V}}}_{{xx}}^{2\omega }\), \({V}_{{xy}}^{2\omega }\). Note that, the second harmonic transport behavior contains two parts: 1) a magnetic-field-independent offset, and 2) the magnetic-field-dependent \(\Delta {V}^{2\omega }\) which can be obtained via subtracting a constant offset value at B = 0 T. Based on these different contributions, the nonlinear response signals have different \(T\) – dependence, e.g., the Berry curvature dipole is a \(T\) – even term while the Drude and quantum metric are \(T\) – odd terms40. Therefore, the Dmetric-induced term can be, in principle, obtained via analysing the magnetic field dependence of the second harmonic transport properties. After subtracting the \(T\) – even term of each measured curve in Sample 1,\(\,{\Delta V}_{{xx}}^{2\omega }\), \({\Delta V}_{{xy}}^{2\omega }\) are obtained and plotted in Fig. 2E, F.\(\,{\Delta V}_{{xx}}^{2\omega }\) and \({\Delta V}_{{xy}}^{2\omega }\) show nonlinear behavior with magnetic field, which are odd functions and appear to saturate at sufficiently large fields. Hence, it is highly possible that both DBC and Dmetric contribute to the nonlinear transport behavior. Further, we summarize the longitudinal and transverse nonlinear response at B = 0, ± 1 T values as functions of the a.c. density (I-V) in Fig. 2H, I, for Sample 1. The parabolic fitting curves show the current dependency of the second harmonic transport signals and clearly indicate the signature of a second-order electronic transport response. The splitting at different fields shows the tuneability in the (DBC and Dmetric) co-contribution model.
In the co-contribution model of the DBC and Dmetric, symmetry breaking is present and is induced by the in-kagome-plane antiferromagnetic alignment. As shown in Fig. 1B, with flat-band type antiferromagnetism, \(P\) and \(T\) symmetries are both broken, and with chiral antiferromagnetism, the \(T\) and \({C}_{3}\) symmetries are broken. A nonzero quantum metric dipole Dmetric may therefore give rise to the odd-with-magnetic-field nonlinear responses, on top of the magnetic-field-even components contributed by DBC. In contrast with sample 1, the responses in Sample 2 are substantially weaker and exhibit a different field dependence (Figure S5), implying these nonlinear responses originate from the magnetic configurations. Before moving on to further discussion, extrinsic effects should be considered. First, we employed a scaling analysis6,9,10 to reveal that the second harmonic Hall conductivity (in the high-field plateau area of Fig. 2F) is not proportional to the relaxation time squared (τ2) in the Drude model, excluding non-linear Drude scattering as the main contribution to the signal. Our analysis clearly showed a primary Dmetric contribution to the T-odd response as well as a contribution from another extrinsic mechanism e.g., second-order skew scattering, side-skew scattering41,42. (See details in Supplementary Information Figure S11, S12) Finally, the current density applied in this study is also smaller than other nonlinear transport research in FIB-based devices13,43,44,45; considering the comparable resistivity in these metallic materials, the Joule heating effect contribution is negligible. Then to understand these nonlinear transport behaviors near the spin reorientation region, the temperature, magnetic field and a.c. density dependent measurements are conducted in both samples.
The SR is triggered by an increase in the Tb single ion anisotropy energy with cooling16,19, which favours the c axis and consequently forces the Mn moments to rotate in the antiparallel (-c in this case) direction. Since the spontaneous TSR is near room temperature, an applied magnetic field will also easily alter the spin configuration in this temperature range. Moreover, in this region, the energies of different magnetic configurations are comparable, thus offering the potential for skyrmion formation, which also contributes to the nonlinear transport responses. Although the nonlinear transport is insignificant when the magnetic field is applied in the basal plane (Sample 2) compared with B along the c-axis, peaks in \({\Delta {\rm{V}}}_{{xy}}^{2\omega }\) with ~ 40% intensity of Sample 1 maximum are observed around the field-induced SR region in sample 2 (Figure S5). To directly compare, the field-dependent second harmonic Hall effect components (see Supplementary Figs. S6, S7 for details) are plotted into a four-dimensional color map in Fig. 3A. Low field features (indicated with a purple arrow), which are approximately the same intensity appear in both sample 1 and 2 (e.g. B applied out of basal plane and in basal plane, respectively). These features appear at different temperatures depending on the sample and are consistent with a field-driven spin reorientation.
Fig. 3: Second harmonic transport in TbMn6Sn6.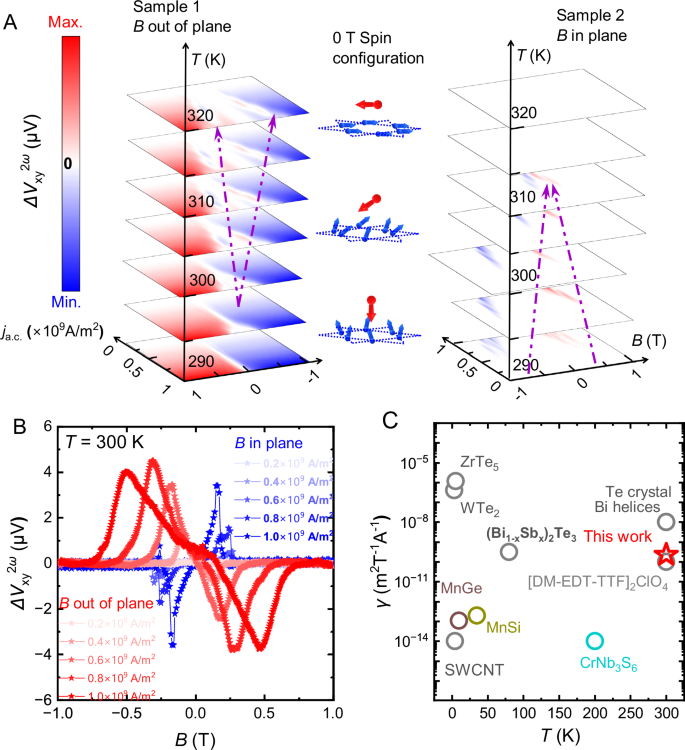
A The magnetic field dependent components of second harmonic Hall effect (\({\Delta V}_{{xy}}^{2\omega }\)) in Sample 1 and Sample 2 are summarized in 4D color map, in which the temperature (T) -, magnetic field (B) -, alternating current (a.c.) density- axes, as well as the color code are all in the same scale for both samples at all temperatures. The purple arrows indicate the field induced spin reorientation transition. The schematic in Panel A, indicating the spontaneous spin orientation transition, shows the nominal spin configurations at 320, 310 and 290 K (top – down), in which the red and blue arrows indicate Tb and Mn moments, respectively. Note that, large external fields will induce the reorientation transitions, and force the moments mostly to align along the applied fields. B The second harmonic Hall voltage related to the chiral magnetic structure. C The electric magnetochiral anisotropy coefficients from some popular quantum materials11,45,54,55,56,57,58,59,60 are summarized at different temperatures, in which the room-temperature maximum value observed in TbMn6Sn6 is highlighted. Note that, the non-tuneable compounds are plotted in grey circles, and the materials that show tuneable nonlinear transport behavior are plotted using different colors (same with the colored labels).
To further study the nonlinear response from the spin reorientation, Fig. 3B shows a plot of \({{\rm{V}}}_{{SR}}^{2\omega }\), which is the SR-related second harmonic Hall component (see SI for \({{\rm{V}}}_{{SR}}^{2\omega }\) calculation and its temperature, magnetic field and a.c. density dependency). As shown in Fig. 3B, the “peak” values (~ 4.5 µV for Sample 1 and ~ 3.5 µV for Sample 2) at 305 K for both samples are comparable, indicating a similar underlying 3D-like mechanism. In Fig. 3A, a naïve model demonstrates the nominal spin configuration. Moreover, from the phase diagram shown in Fig. 3A, the quantum metric effect and skyrmion related eMChA can be isolated below 300 K. Namely with the field applied along the c axis and along the a axis, only one effect is detected in each case (quantum metric and skyrmion eMChA, respectively).
To interpret these results, it is useful to consider the rich magnetism presented in TbMn6Sn6. Recent neutron scattering experiments17,19,46 suggest that on top of the long-range ferromagnetic ordering in the Mn kagome layers, antiferromagnetic chiral magnons exist. Our magnetic study (Figure S2) also suggests the existence of in-kagome-plane Mn moment components in the studied region, which is necessary for the presence of in-plane antiferromagnetism. Moreover, Lorentz transmission electron microscope experiments33,47 have confirmed the existence of skyrmions in TbMn6Sn6 at room temperature, which can be manipulated by the physical environments, e.g., temperature, magnetic fields and focused electron beam. The observed peaks in Fig. 3A are in comparable temperature and field range, which further suggests its relationship with topological spin textures. Skyrmions can be also driven by applied electric current, e.g., in the topological magnet MnSi48, which leads to the deformation of skyrmions and therefore, the real-space Berry phase. Thus, the a.c. density induced peak shifts in the Fig. 3B and Figures S6, 7 can be understood using this framework. The current-induced skyrmions dynamics shows clear “turn-on” effect, e.g., with 0.2×109 A/m2 applied current, there are no obvious skyrmion peaks; while in the same condition, the Dmetric induced plateaus are robust. Further, the antiferromagnetic chiral magnons contain in-plane and out-of-plane components19, which support 3D skyrmion dynamics, and thus contribute to the 3D-like behaviour in Fig. 3B. Therefore, TbMn6Sn6 is a chiral magnet near the spin-reorientation region which could give rise to a strong eMChA effect in the second harmonic Hall response.
Based on these results, there are clearly two distinct mechanisms that contribute to the large field-dependent nonlinear response near room temperature. The first is the eMChA effect arising from the field-induced spin reorientation of the chiral magnetic structure around the spin reorientation temperature. Due to the three-dimensional nature of the skyrmions (real-space topology) in this material, the effect is observed with both out-of- and in-kagome plane applied fields. The second contribution is from the electronic band structure (Dmetric and DBC), which arises only when B // c (Figure S9). After ruling out the current heating contribution, Drude contributions, the intrinsic anisotropic nonlinear transport result can be understood by considering the symmetry in the material.
The quantum metric can arise in a material with broken \(P\) and broken \(T\) symmetry. The symmetry breaking depends on in-plane antiferromagnetism, and is supported by a slight canting of the moments (~13o)29. Therefore, this broken \(P\) and broken \(T\) symmetry is only present when B // c-axis. When B // basal plane, the parallel alignment of the Mn moments in the kagome lattice will no longer break \(P\) symmetry, and thus only skyrmion-induced components are observed in Sample 2. In this scenario, the nonlinear response can be easily controlled via changing temperatures or applied fields in room temperature region. The magnetic structure induced symmetry breaking phase is an important starting point to realize nonlinear electronic properties in quantum materials. A good example is intrinsic magnetic topological insulator MnBi2Te4, in which Mn moments are out-of-plane ferromagnetically coupled in each layer, and antiferromagnetically between adjacent layers below Néel temperature TN. Below TN, odd-layer MnBi2Te4 breaks both \(P\) and \(T\) symmetries, however preserves PT symmetry, offering suitable material system to study quantum metric physics6. Experimentally10, Dmetric induced nonlinear transport has been observed below TN. While another group shows additional symmetry manipulation via van de Waals engineering boosts the Dmetric contribution to nonlinear responses. The antiferromagnetism in MnBi2Te4 orders at cryogenic temperatures, and has high defect density level that may reduce the efficiency in symmetry manipulation. TbMn6Sn6 has above-room-temperature magnetism, and high crystalline quality, thus it can be an ideal platform for quantum metric physics. Recently, the studies of quantum metric induced physics at room temperature in WTe249, Mn3Sn50 and Cs2Ni3S451 are attracting significant attention, indicating a promising stage for implementing quantum geometry in electronic devices.
A substantial room temperature nonlinear response is a key requirement in designing highly-efficient nonlinear devices. Recently, a large DBC has been demonstrated using second harmonic transport at room temperature in topological materials such as the Weyl semimetal TaIrTe452, the massive Dirac semimetal BaMnSb245, and Bi thin films53. In addition to room temperature operation, another key requirement for emerging devices is tuneability, which has been reported in a symmetry breaking phase in the kagome CsV3Sb5 compound, although only at cryogenic temperatures13. In Fig. 3C, the coefficient of eMChA, \(\gamma={4V}^{2\omega }/({V}^{\omega }B{j}_{a.c.})\) in some popular materials are summarized, together with our work on TbMn6Sn6. Among all of the materials, TbMn6Sn6 is the only one which demonstrates giant, tuneable second harmonic transport behavior at room-temperature.
We have shown that in TbMn6Sn6, the Berry curvature dipole, quantum metric dipole and skyrmion induced second harmonic transport behavior coexist at room temperature, and can be tuned via control of the magnetic configurations. The giant and tuneable effect is confirmed in multiple samples, thus promoting a room temperature controllable response of the nonlinear physics for device design. The rich physics of kagome materials may prove a fertile playground to identify other quantum metric driven non-linear responses, which could open a new direction in practical nonlinear device design for next-generation electronics and spintronics.