As observed in the Heusler alloys, atomic disordering plays a critical role in insulating tunnel barrier materials of MTJs. The examples involve spinel-type oxides AB2O4, the particular of which are advantageous in terms of lattice-well-matched heterointerface of bcc-based ferromagnetic materials with a high TMR ratio and/or low resistance-area product (RA)34,35,36,37. The physical properties of TMR junctions desired for spintronic applications can be potentially addressed by wide variations of constituent elements, e.g., their compositions and atomic disordering. To tackle such complexity, data-driven material design has opened a new era of materials science, but materials exploration using conventional machine learning models, such as Bayesian optimisation and Monte Carlo tree search, can make efficient materials exploration difficult due to the combinatorial explosion resulting from the large number of degrees of freedom in the materials themselves.
To address the abovementioned issue, an alternative approach is introduced here, which is not to use only first-principles calculations and machine learning, but to further combine them with quantum annealing (QA) that is inspired from quantum computing technologies recently available. Focusing on atomic disordering of MgGa2O4 of an MTJ for example, namely Fe/atomic-disordering MgGa2O4/Fe(001) system, we demonstrate a proof-of-concept study to search for suitable MTJs in terms of energetically stable (lower \(\Delta {E}_{{\rm{Total}}}\)), higher TMR ratios and lower RA figures by optimising an atomic arrangement of Mg and Ga of MgGa2O4 tunnel barrier.
In the MTJ with inverse-type spinel MgGa2O4 as shown in Fig. 9a, all the Mg and half the Ga atoms randomly occupy the octahedral site (orange sites in Fig. 9a) and the remaining Ga atoms occupy the tetrahedral site (green sites in Fig. 9a). In this work, the atomic arrangement of Mg and Ga at the octahedral sites, in which the number of total combinations can be defined as \({10}_{{C}_{5}}= 252\), can be optimised by first-principles calculations of density functional theory (DFT), machine learning and QA techniques. In the QA-based framework, the combinatorial optimisation problem is replaced with an Ising model, and the QA obtains the lowest Ising energy of the given Ising Hamiltonian, which describes well the relationship between physical properties and materials expressed by quantum bits (qubits). An Ising model Hamiltonian can be constructed by using a machine learning, so-called factorization machine (FM)38. In the FM model, the target property of interest can be expressed by atomic arrangement of Mg and Ga as follows:
$$f({\boldsymbol{x}})=b+\mathop{\sum }\limits_{i=1}^{N}{q}_{i}{x}_{i}+\mathop{\sum }\limits_{i=1}^{N-1}\mathop{\sum }\limits_{j=i+1}^{N}\langle {v}_{i},{v}_{j}\rangle {x}_{i}{x}_{j},$$
(4)
where \(N\) is the number of qubits corresponding to disordering sites [\(N=10\) in this work as shown in Fig. 9a] and a vector \({\boldsymbol{x}}={\boldsymbol{\{}}{x}_{1},\,{x}_{2},\,\ldots ,\,{x}_{N}{\boldsymbol{\}}}\) is a descriptor defining an atomic arrangement of Mg and Ga (\({x}_{i}=0\) for Mg and \({x}_{i}=1\) for Ga at disordering site \(i\)). The fitting model parameters are bias term \(b\), linear term \({q}_{i}\) and quadratic term \(\langle {v}_{i},{v}_{j}\rangle ={\sum }_{k}^{K}{V}_{ik}{V}_{jk}\). A hyperparameter \(K\) determines a rank of FM model and optimised to be 7, 2, and 3 for the optimisation of \(\Delta {E}_{{\rm{Total}}}\), TMR, and RA, respectively, in this work. The fitted model parameters, \({q}_{i}\) and \(\langle {v}_{i},{v}_{j}\rangle\), can be transformed into the quadratic unconstrained binary optimisation (QUBO) form to solve the Ising model by the QA as below:
$$\begin{array}{rcl}{Q}_{ij}=\left\{\begin{array}{l}{q}_{i}\,(i=j)\\ \langle, {v}_{i},{v}_{j}\rangle \,(i\,\ne \,j)\end{array}\right.\end{array}.$$
(5)
Fig. 9: Modelling and calculation processes on MTJs.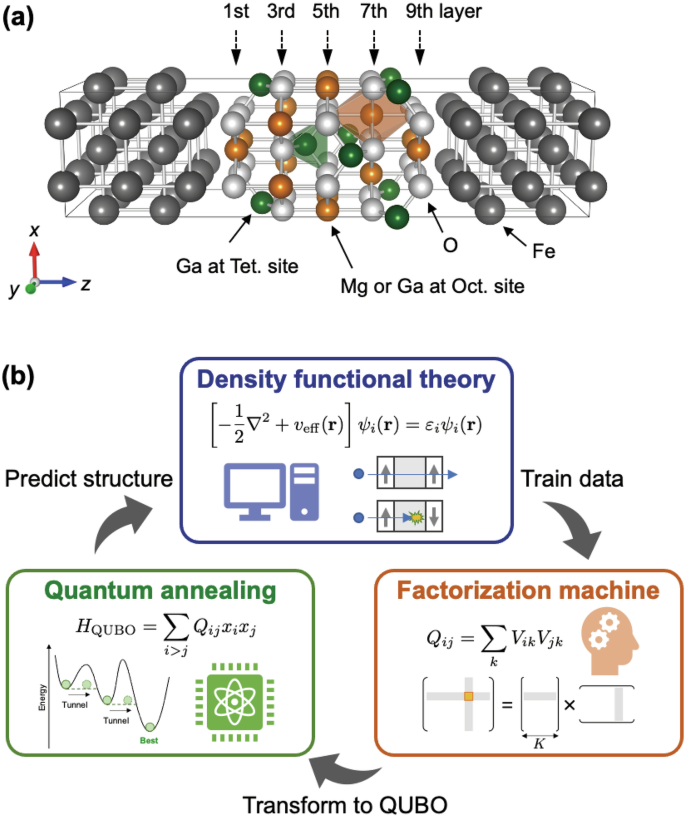
a MTJ structure of Fe/atomic-disordering MgGa2O4/Fe(001), where Mg and Ga atoms randomly occupy octahedral site (orange site). b Frow of calculations combined with QA, FM, and DFT40.
The Ising Hamiltonian called HQUBO is then given as
$${H}_{{\rm{Q}}{\rm{U}}{\rm{B}}{\rm{O}}}=\mathop{\sum }\limits_{i
(6)
The first term is a cost function, and the second term is a penalty term to constrain the atomic composition of Mg and Ga to be 1:1. A hyperparameter \(\alpha\) (real number, \(\alpha > 0\)) is to control the strength of penalty term. The QA solves the HQUBO and the solution with the lowest Ising energy is the next candidate of Mg/Ga atomic arrangement for which target physical property should be evaluated by the DFT calculations. The total energy, ground-state electronic structures, and spin-transport properties are obtained from first-principles calculations with the basis of linear combination of atomic orbitals, implemented in the Quantum Atomistix Toolkit (Quantum-ATK) simulation39. The GGA is employed for the exchange-correlation functional18, For the details of calculations method, refer to ref. 40. Our calculation flow, FM + QA + DFT, is shown in Fig. 9b. The FM + QA + DFT is referred to FM + QA (DFT is omitted) hereafter.
In Fig. 10, the results of FM + QA of the searching history to obtain the suitable MTJ are shown for the \(\Delta {E}_{{\rm{Total}}}\), TMR, and RA. To investigate an effectiveness of FM + QA, FM + simulated annealing (FM + SA), FM + exact solver (FM + ES) (In the FM+ES, the Ising energy is evaluated for all the atomic arrangements (x’s) of the training data, and then the vector x giving the lowest Ising energy is always selected as the next candidate.), Bayesian optimisation (BO), and random search (RS) were also performed, where 10 trials were carried out using different initial training datasets that include randomly selected 20 MTJ structures. For the \(\Delta {E}_{{\rm{Total}}}\), as shown in Fig. 10a the FM + QA obtains successfully the suitable MTJ within approximately 50 structures (including the training data of 20 structures), and this is comparable to that of FM + ES (Fig. 10c), verifying our FM + QA method. The efficiency obtained from the FM + QA is slightly faster than the FM + SA (see Fig. 10b) and significantly than the BO and RS (see Fig. 10d, e). For the TMR, similar searching efficiency is obtained among FM + QA, FM + SA, and FM + ES (Fig. 10f–h), and this efficiency is much better than those of BO and RS (see Fig. 10i, j). From these results, thus, the FM + QA might be a promising approach in the search for the preferred MTJ with the energetically stable atomic disordering and the highest TMR property.
Fig. 10: History of the calculated number of structures required to obtain the best MTJ structure.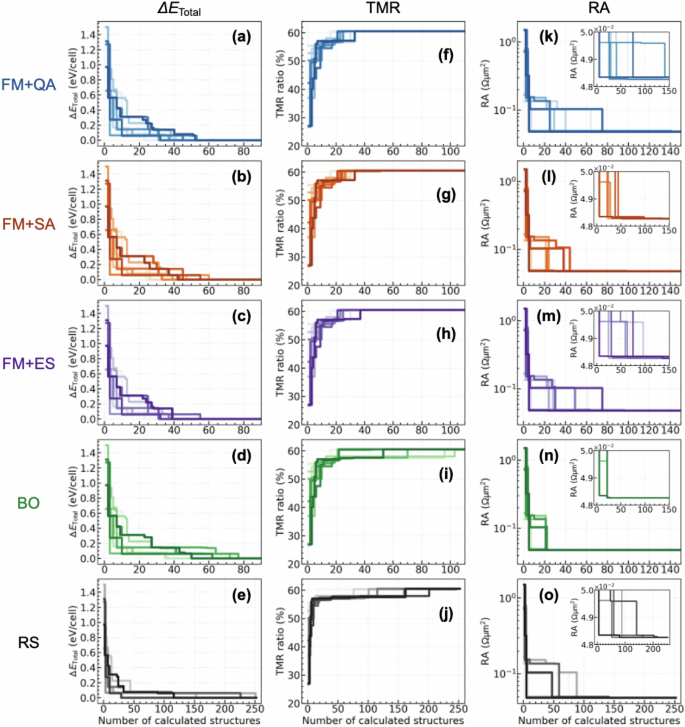
a–e \(\Delta {E}_{{\rm{Total}}}\), (f)–(j) TMR, and (k)–(o) RA obtained by FM + QA, FM + SA, FM + ES, BO, and RS, respectively. In each property and method, 10 trials were carried out by using the training dataset including 20 MTJ structures. The horizontal axis includes those initial training dataset, the range of which is different between the RS and others40.
On the other hand, there remains a difficulty in optimising the atomic arrangement for MTJs with lower RA by using FM + QA. Figure 10k shows that the variation of the number of structures required to be optimised is very wide, depending on the initial training datasets, with a maximum of over 150 structures required (see the inset). This feature is confirmed even in FM + SA and FM + ES (see Fig. 10m, n). These results seem to reflect the inaccuracy of the FM training, from which the HQUBO is constructed, rather than the performance of QA solver. Therefore, it is difficult to reach an optimal solution, i.e., an MTJ with lower RA, from such HQUBO. In contrast, the BO efficiently reaches the best MTJ with the lowest RA.
Here potential solutions to improve the robustness of the FM model for RA optimisation are discussed. One may obtain better performance of FM model with the hyperparameter K greater than K = 10, although the K is set to 3, yielding the best performance from a pre-test validated within K = 1 ~ 10 in this proof-of-concept study. Additionally, the size of database used in this demonstration, i.e., 20 training data, may be too small and/or too sparce to adequately train the relationship of the RA and atomic arrangement in the FM model. The latter would be more serious in defining the generalisability of FM model, but should be mitigated in a natural way at the practical level of FM + QA( + DFT), where combinatorial explosion occurs, so that the number of training dataset is expected to be larger than that of this demonstration. Furthermore, in a real problem, finding several good material candidates is beneficial for device developments by materials informatics, rather than finding only one best solution. In this context, our demonstration, although still inferior to BO, achieves efficient search performance comparable to those of \(\Delta {E}_{{\rm{Total}}}\) and a TMR ratio for RA optimisation (see searching efficiency results denoted as “RA*”, in Fig. 4 of ref. 37).
To conclude, we propose an alternative approach adaptable to combinatorial explosion problems by combining state-of-the-art QA, FM, and DFT techniques and applied it to optimisation problem of an atomic disordering in MTJs with spinel-oxide tunnel barrier, MgGa2O4. Our proof-of-concept study achieved higher searching efficiency in particular physical properties compared to the conventional machine learning, such as Bayesian optimisation, while leaving room for improvement of our method. The present approach may offer a breakthrough to overcome the combinatorial explosion, which is inaccessible to conventional machine learnings regardless of whether the system is ordering and disordering. More specifically, the FM + QA + DFT is applicable to multi-component materials such as Heusler alloy families once the combinatorial optimisation problem of atomic elements, compositions, defects, crystal structures, and other degrees of freedom of interest can be mapped onto the Ising model.