Previous studies have shown that Fe5GeTe2 has two crystal structures27,30, one with higher symmetry in space group R\(\bar{3}\)m (No.166) and the other in space group R3m (No.160). This study focuses on the Fe5GeTe2 structure in the R3m space group to investigate the nonlinear Hall effect. Understanding the crystal structure of Fe5GeTe2 is crucial before studying the nonlinear Hall effect. The crystal structure of Fe5GeTe2 is characterized by its non-centrosymmetric space group R3m, with lattice parameters a = b = 4.037 Å and c = 29.194 Å. The structure exhibits repetitive building blocks arranged along the c-direction and offset in accordance with the R-centered space group. The rhombohedral lattice of the structure contains three Fe5GeTe2 monolayers within each unit cell (Fig. 1a). In terms of monolayers, Fe5GeTe2 monolayers are composed of four distinct atomic layers arranged in a sandwich structure with the sequence A-B-C-B’-D-A’. The atoms within the Fe-Ge layer (C) and Fe layer (D) adopt a positive hexagonal arrangement. The (C) layer is situated between the Fe atomic layer (B-B’), resulting in a van der Waals gap due to the outermost layer consisting of Te atoms. The crystal structure exhibits threefold helical symmetry axes and threefold rotational symmetry axes, effectively suppressing the BCD (Fig. 1b and Figure S1)31,32.
Fig. 1: Crystal structure and crystal growth of Fe5GeTe2.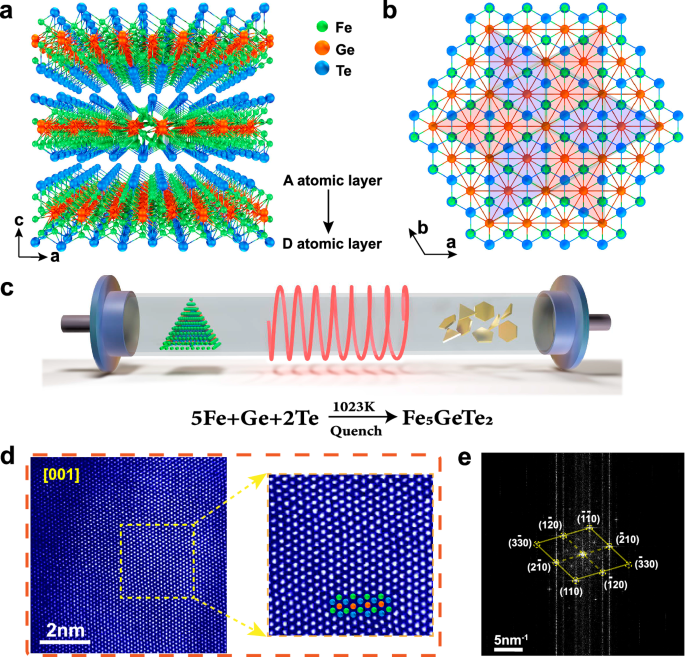
a Crystal structure of Fe5GeTe2 viewed along the [110]. b The crystal structure of Fe5GeTe2 from the top view. The fragment describes the red-purple shaded area as the threefold helical symmetry axes (31, 32). green sphere: Fe atoms, orange sphere: Ge atoms, blue sphere: Te atoms. c Schematic diagram of the growth of high-quality Fe5GeTe2 single crystals. d STEM image of Fe5GeTe2. e STEM image corresponding fast Fourier translate (FFT) pattern.
Centimeter-sized single crystals of Fe5GeTe2 (Figure S2, Fig. 1c) were successfully synthesized via a solid-state reaction with the addition of a mineralizing agent (I2) (see Experimental section for details). The atomic structure of few-layer Fe5GeTe2 nanosheets along the (001) plane (Fig. 1d) was confirmed by atomic-resolution annular dark field scanning transmission electron microscopy (ADF-STEM), in which the corresponding fast Fourier transfer (FFT) pattern, as shown in Fig. 1e, reflecting the high crystal quality of the nanosheets. The XRD pattern of Fe5GeTe2 crystals (Fig. 2a) shows a predominant scattering vector perpendicular to the (110) plane due to its layered structure, consistent with a previous study30. Fe5GeTe2 atomic layers can be obtained through micro-mechanical exfoliation of bulk crystals using adhesive tape, facilitated by the weak van der Waals interlayer coupling. The energy dispersive X-ray spectrum (EDS) results show the elemental atomic ratio of Fe, Ge and Te in as-synthesized crystals are 5.4: 1: 1.9 (Figure S3), basically consistent with the stoichiometric ratio of Fe5GeTe2. In addition, the EDS mapping (Figure S4) also confirms good distribution uniformity of our synthesized crystals. The X-ray photoelectron spectroscopy (XPS) integrated peak areas, corrected using sensitivity factors (Figure S5), yielded a Fe: Ge: Te atomic ratio of approximately 4.6: 1: 1.9. This composition shows negligible deviation from the nominal Fe5GeTe2 stoichiometry determined by EDS. Second harmonic generation (SHG) spectroscopy confirmed the inversion symmetry breaking in few-layer Fe5GeTe2 using an 850 nm laser to generate a stable SHG signal at 425 nm (Fig. 2b). The image of the SHG mapping distinctly delineates the sample region, providing compelling evidence for the inversion symmetry breaking in Fe5GeTe2 (Figure S6).
Fig. 2: Characterization of Fe5GeTe2.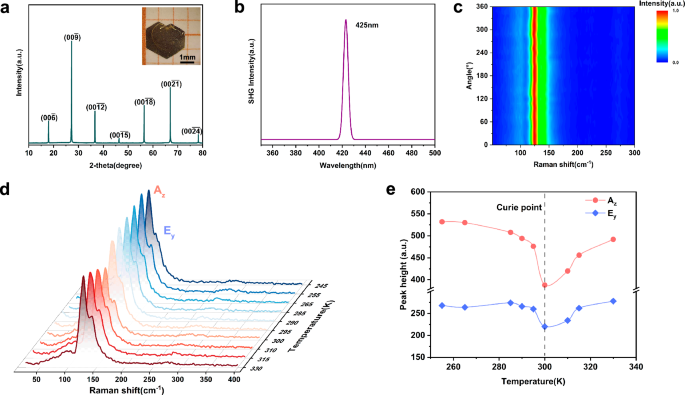
a Experimental X-ray powder diffraction (XRD) patterns for Fe5GeTe2 crystals Inset: optical images of Fe5GeTe2 single crystal. b The SHG signal of Fe5GeTe2 under illumination of 850 nm laser. c Colorful contour mapping of the polarized Raman spectra, where the color reflects the intensity of the Raman vibration. d Temperature-dependent Raman spectrum of Fe5GeTe2. e Correlation between temperature and peak height of Raman peaks at different wavenumbers in Fe5GeTe2.
The vibrational properties of Fe5GeTe2 originate from the interactions between elementary excitations and phonons. However, as a newly discovered van der Waals magnet, the experimental Raman spectrum of Fe5GeTe2 has not yet been reported so far. In this study, we systematically investigated Raman vibrational modes using the density functional theory (DFT) calculations (Figure S7) and Raman spectroscopy (Fig. 2c) with a 532 nm laser. Based on Fe5GeTe2 belonging to space group R3m and point group C3v, group theory analysis reveals the presence of three distinct nonzero vibrational modes, specifically the Az, Ex, and Ey modes (Note. S6). According to measurements (Fig. 2c), there were only two Raman active peaks, located at 125 cm−1 (Az) and 141 cm−1 (Ey) for bulk Fe5GeTe2, in agreement with the calculated modes (Figure S7). The thickness-dependent Raman spectra exhibit pronounced blueshifts of approximately 3–5 cm−1 for both AZ and Ey modes as the thickness decreases from 18.8 nm to 9.2 nm, suggesting robust interlayer interactions and hybridization effects within Fe5GeTe2 (Figure S7). Given the challenges associated with directly measuring the magnetism of atomically thin magnetic materials, the changes in Raman spectra accompanying magnetic transitions provide a viable alternative method for monitoring the magnetic order in such materials. It is well known that bulk Fe5GeTe2 has a high Curie temperature of 310 K, while atomic layer samples have an intrinsic Curie temperature of 280 K, near room temperature27. To elucidate the correlation between Raman spectra and the ferromagnetic phase transition at the Curie point of Fe5GeTe2, Raman spectra were acquired for film samples in the vicinity of this critical temperature, as illustrated in Fig. 2d. A significant reduction in the Raman peak intensity of Fe5GeTe2 is observed upon cooling to 300 K (Fig. 2e), which corresponds to the Curie point of the sample. Beyond this critical temperature, the peak intensity recovers, progressively returning to its initial value. These variations in peak intensity are indicative of the material’s transition from paramagnetic to ferromagnetic states. To further confirm the magnetic properties of Fe5GeTe2, we combined magneto-optic effect characterization (reflection magnetic circular dichroism, RMCD) with electronic transport measurements probing the anomalous Hall effect (Figure S8). Both methods consistently demonstrate ferromagnetic ordering in Fe5GeTe2, exhibiting a Curie temperature of approximately 300 K.
To evaluate the nonlinear transport properties of Fe5GeTe2, a Hall bar device was fabricated using a few-layer Fe5GeTe2 nanoflake on a SiO2/Si substrate (280 nm oxide layer) (Fig. 3a, b, Note. S8), hexagonal boron nitride (h-BN) as the top protective layer, and classical six-symmetric metal contact electrodes consisting of 10 nm Ti and 90 nm Au, through the processes of laser direct writing (LDW) and electron beam evaporation (see Experimental section for details). The utilization of a lock-in amplifier (LIA) alternating current (AC) technique was implemented to measure the nonlinear transport characteristics of the device, with the primary objectives of noise suppression and acquisition of higher order signals. To study the nonlinear Hall effect, a low-frequency (ω = 7.777 Hz) alternating voltages \({V}_{\parallel }^{\omega }\) was applied to the device along the longitudinal direction under zero magnetic field, the direction transverse voltages \({V}_{\perp }^{n\omega }\) with the second-harmonic 2ω and third-harmonic 3ω frequencies can be measured by a lock-in amplifier in a phase-sensitive way (Fig. 3b and inset of Fig. 3c). Before monitoring nonlinear Hall signals, it is important to eliminate any spurious signals caused by errors. Our devices demonstrate good ohmic contacts between the material and electrodes (Figure S11), suggesting that the potential errors, such as the Schottky rectification effect, will not impact any measured nonlinear Hall signals. In addition, nonlinear signals from drive currents at different frequencies are examined to detect and remove artifacts caused by capacitive coupling, as shown in Figure S12. During measurements, the first-, second-, and third-order nonlinear signals were acquired by monitoring the lock-in amplifier’s phase near 180°, 90°, and 180°, respectively (Figure S13). This study tested numerous Fe5GeTe2 Hall devices to confirm the presence of third-order nonlinear Hall signals (Figure S14), providing further evidence that these signals are not random. While earlier research33,34,35 has found that time-reversal symmetry breaking is needed for the first-order response, leading to an anomalous Hall effect without an external magnetic, recent advances10,23,24 reveal that such responses can also arise from intrinsic resistive anisotropy in materials. Fe5GeTe2 was tested for its first-order response (Figure S15), but due to its specific symmetry, the cause of this response was not analyzed in detail. The transverse response voltage (\({V}_{\perp }^{\omega }\)) is linearly related to the longitudinal excitation voltage (\({V}_{\parallel }^{\omega }\)) under fundamental frequency conditions, indicating good ohmic contact.
Fig. 3: Observation of nonlinear transport in Fe5GeTe2.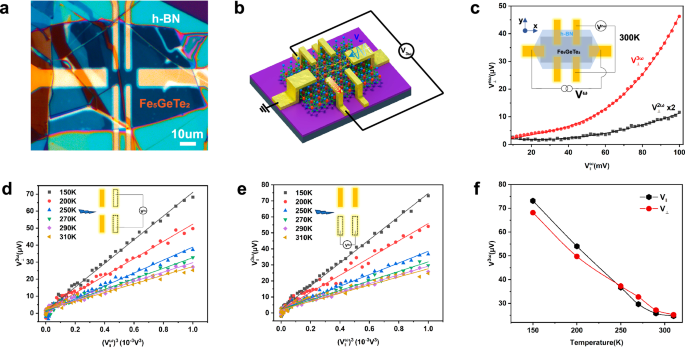
a The optical image shows a Fe5GeTe2 Hall device with six electrodes, which are protected by h-BN at 100X magnification. b The schematic view of the Fe5GeTe2 Hall device. The nonlinear signals are measured in the direction indicated. c Second and third order signal \({V}_{\perp }^{n\omega }\) as a function of \({V}_{\parallel }^{\omega }\) when the driving field is applied along a specific direction at room temperature. Inset: schematic diagram of second and third order signal measurements. d The \({V}_{\perp }^{3\omega }\) signal as a function of the \({({V}_{\parallel }^{\omega })}^{3}\) at different temperatures from 150 to 310 K. Inset: Schematic representation of the direction of the applied excitation voltage and the direction of the detected signal. e The \({V}_{\parallel }^{3\omega }\) signal as a function of the \({({V}_{\parallel }^{\omega })}^{3}\) at different temperatures from 150 to 310 K. Inset: Schematic representation of the direction of the applied excitation voltage and the direction of the detected signal. f The relationship between \({V}_{\perp }^{3\omega }\) and \({V}_{\parallel }^{3\omega }\) with temperature is shown when \({V}_{\parallel }^{\omega }\) = 0.1 V.
We detected second- and third-order nonlinear Hall effects in the device, with the third-order signal being ten times stronger than the second-order signal, indicating the dominance of the third-order effect in Fe5GeTe2. This trend was consistent across all devices (Figure S16). Theoretical analysis of crystal physics was utilized to derive the second-order and third-order currents in Fe5GeTe2 (see Experimental section for details). It was found that all second and third-order currents in the R3m space group can appear in the a-b plane, but third-order currents are not allowed in the out-of-plane direction. The third-order nonlinear current in the crystal must satisfy symmetry constraints23, with the third-harmonic response exhibiting a twofold angular dependence relative to θ (Figure S17). The crystal axis determined through this fitting procedure shows perfect alignment with the C3v point group of the space group R3m (see Experimental section for details). The excellent agreement between the theoretical calculations and experimental data further confirms that the nonlinear transport behavior in Fe5GeTe2 is intrinsically governed by its C3v symmetry even in the magnetically ordered state, thereby robustly validating the reliability of our experimental results. It is of significance that a strong third-order signal was detected at room temperature (300 K), a rarity within the realm of third-order nonlinear Hall effect research (Fig. 3c).
Subsequently, we investigated the third-order nonlinear Hall response in Fe5GeTe2. In the context of symmetry, the first-order Hall response requires the broken time-reversal symmetry, the second-order Hall response requires the broken inversion symmetry14,15,36, and the third-order Hall response requires the maintenance of time-reversal symmetry while simultaneously breaking the inversion symmetry10,23. Fe5GeTe2 does not follow the same rules as other materials because its time-reversal (T) and inversion (P) symmetries are broken, but the nonlinear Hall response can still occur with breaking time-reversal symmetry. Recent studies17,20,21 have demonstrated that quantum geometry can be segmented into two components: a real part referred to as the quantum metric, and an imaginary part known as the Berry curvature. Both factors play a role in nonlinear transport. The three-fold rotational symmetry intrinsic to Fe5GeTe2 suppresses BCD contributions21, which may allow the QMD to emerge as the dominant intrinsic mechanism for the nonlinear Hall response. Data in Fig. 3 were collected from #Device 4 with samples thicker than 100 nm to increase the ferromagnetic transition temperature above room temperature (Tc = 310 K)27, making it easier to observe the third-order nonlinear transport of the quantum metric contribution at room temperature. When an excitation voltage is applied to the Hall device, third-order signals are produced and can be measured in both longitudinal and transverse directions (Fig. 3d, e). When the excitation voltage (\({V}_{\parallel }^{\omega }\)) is constant, \({V}_{\parallel }^{3\omega }\) and \({V}_{\perp }^{3\omega }\) have similar intensities. As temperature decreases, their magnitudes gradually increase (Fig. 3f). The nonlinear Hall effect caused by the BCD exclusively generates a transverse nonlinear response (perpendicular to the excitation current)14,15. In contrast, the QMD enables both transverse and longitudinal nonlinear transport20,21. In experiments, we observed a decrease in signal strength at high temperatures above the Curie temperature, but small third-order signals were still detectable (Figure S18). The observed phenomena may be attributed to disorder-induced scattering mechanisms. Recent studies37,38,39,40,41 highlight that extrinsic scattering (e.g., skew scattering and side-jump) plays a critical role in nonlinear Hall effects, even dominating their behavior in certain regimes. Consequently, a rigorous analysis of scattering contributions in Fe5GeTe2 is essential.
As previously discussed, nonlinear Hall effects can be attributed to the BCD, the QMD, or scattering (non-intrinsic origin). To examine the specific microscopic mechanism of the third-order nonlinear response in Fe5GeTe2, we are investigating the correlation between the third-order response and the scattering time (τ). Due to its metallic nature, the longitudinal conductance of Fe5GeTe2 remains unaffected by the application of an external gate voltage. Therefore, the scattering time can be altered by adjusting the sample temperature. Liquid helium (He) was utilized as a cooling agent to examine the relationship between scattering time and third-order signals in challenging environments. Among these, the device in Fig. 4 (labeled #Device3, 50 nm thickness) was a representative example of this analysis. The resistance was quantified utilizing the four-terminal technique, with conductivity calculated using the formula \(\sigma \,=\,\frac{{GL}}{S}\), where L represents the distance between opposing electrodes and S denotes the cross-sectional area of the channel. Fe5GeTe2 demonstrates metallic transport properties, as illustrated in Fig. 4a. The relationship between temperature and conductivity is found to be insignificant above 100 K, with σ (300 K) ≈ 0.5σ (30 K), consistent with previous reports27. Consistent with previous findings at temperatures ranging from 150 to 300 K, the variable \({V}_{\perp }^{3\omega }\) exhibits a linear dependence on \({({V}_{\parallel }^{\omega })}^{3}\) at all temperatures, as depicted in Fig. 4b. The linear relationship exhibits a marked deviation when the temperature is reduced below 100 K, and this anomalous behavior cannot be attributed to Berry curvature or scattering mechanisms10,23 as the dominant contributions to the third-order signal, as discussed in detail below.
Fig. 4: Temperature-dependence third-order nonlinear Hall effect measurement results for the Fe5GeTe2.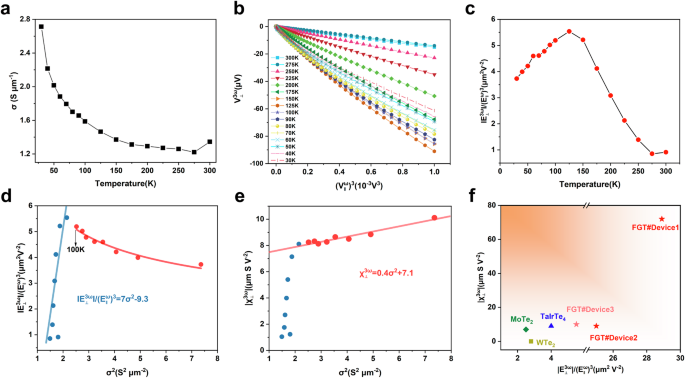
a The longitudinal conductivity σ as a function of temperature. b The dependence of \({V}_{\perp }^{3\omega }\) on the cubic of \({V}_{\parallel }^{\omega }\) is linear within the temperature range of 30 to 300 K. c The \(| {E}_{\perp }^{3\omega }| /{({E}_{\parallel }^{\omega })}^{3}\) as a function of temperature. d\(\,| {E}_{\perp }^{3\omega }| /{({E}_{\parallel }^{\omega })}^{3}\) as a function of \({\sigma }^{2}\) in Fe5GeTe2 but at various temperature intervals, \(| {E}_{\perp }^{3\omega }| /{({E}_{\parallel }^{\omega })}^{3}\) exhibits distinct functional relationships with \({\sigma }^{2}\). e The scaling relationship between the third-order nonlinear conductivity \({\chi }_{\perp }^{3\omega }\) and the square of the linear longitudinal conductivity \({\sigma }^{2}\) The scaling is performed within the temperature range of 30–100 K. f Comparison of the third-order conductivity (\({\chi }_{\perp }^{3\omega }\)) and third-order current conversion ratio (\(| {E}_{\perp }^{3\omega }| /{({E}_{\parallel }^{\omega })}^{3}\)) of Fe5GeTe2 with other materials.
Since \({V}_{\perp }^{3\omega }\) cannot be accurately compared under identical conditions, we instead compare the slopes of the linear relationship between \({V}_{\perp }^{3\omega }\) and \({({V}_{\parallel }^{\omega })}^{3}\). The relationship between voltage and electric field can be quantified using the equations \({E}_{\perp }^{3\omega }\,=\,\frac{{V}_{\perp }^{3\omega }}{{L}_{\perp }}\) and \({E}_{\parallel }^{\omega }\,=\,\frac{{V}_{\parallel }^{\omega }}{{L}_{\parallel }}\), where \({L}_{\parallel }\) and \({L}_{\perp }\) represent the distances between the electrodes in the transverse and longitudinal orientations, respectively. The temperature-dependent scaling relationship between the third-order nonlinear Hall component \({V}_{\perp }^{3\omega }\) and the cubic power of the linear excitation \({({V}_{\parallel }^{\omega })}^{3}\), characterized by the dimensionless ratio \(\frac{| {V}_{\perp }^{3\omega }| }{{({V}_{\parallel }^{\omega })}^{3}}\,=\,\frac{{L}_{\perp }}{{L}_{\parallel }^{3}}\frac{| {E}_{\perp }^{3\omega }| }{{({E}_{\parallel }^{\omega })}^{3}}\), exhibits distinct thermal evolution across different regimes. Above 100 K, this scaling coefficient demonstrates a progressive temperature-dependent suppression that becomes particularly pronounced near the Curie temperature (TC ≈ 290 K). However, the correlation between these voltage components shows a notable decoupling in the low-temperature phase below 100 K, suggesting a fundamental change in the underlying dominant contributions (Fig. 4c). The temperature dependence of the scattering time (τ) in Fe5GeTe2 is found to be significant below 100 K, as illustrated in Fig. 4a, due to the linear relationship between the conductivity (σ) and scattering time (τ). The analysis rigorously investigates the relationship between \(\frac{| {E}_{\perp }^{3\omega }| }{{({E}_{\parallel }^{\omega })}^{3}}\) and σ2 across a temperature range of 30 K to 300 K. A linear relationship is seen between \(\frac{| {E}_{\perp }^{3\omega }| }{{({E}_{\parallel }^{\omega })}^{3}}\) and σ2 at temperatures above 100 K, confirming the scaling relationship:
$$\frac{| {E}_{\perp }^{3\omega }| }{{({E}_{{||}}^{\omega })}^{3}}=\xi {\sigma }^{2}+\eta$$
(1)
where ξ and η are constants. The left-hand expression can be rewritten as the ratio of the third-order nonlinear Hall conductivity to the longitudinal conductivity (\(\frac{| {E}_{\perp }^{3\omega }| }{{({E}_{\parallel }^{\omega })}^{3}}\,\approx \,\frac{{\chi }_{\perp }^{3\omega }}{\sigma }\)), \({\chi }_{\perp }^{3\omega }\) is represented as a third-order nonlinear Hall conductivity. The left side can be rewritten as a ratio of two terms, approximately equal to \({\chi }_{\perp }^{3\omega }\)/σ. By analyzing the scaling law relationship between nonlinear response current and relaxation time, it is feasible to determine the predominant contribution21,37. Typically, τ0 represent QMD contributions, τ signifies the proportion of BCD and side-jump contributions, whereas τ3 denotes the ratio of skew scattering contributions. As shown by the pronounced linear dependence observed in the experimental (blue data points in Fig. 4d) demonstrates that QMD contributions become obscured within this temperature regime (T > 100 K). This suppression primarily arises from the disruption of magnetic domain ordering combined with the competition contributions. Additionally, the BCD in Fe5GeTe2 is suppressed by its inherent C3v symmetry. As a result, under this symmetry constraints, the dominant contributions to the system are governed by Eqs. (2) and (3).
$$\left\{\begin{array}{c}{{J}}_{{side}-{jump}}^{3{{\omega }}}{{\propto }}\,{{\rm{\tau }}}\,{{{\propto }}\,{{\rm{\sigma }}}}\\ {{J}}_{{skew scattering}}^{3{{\omega }}}\,{{\propto }}\,{{\tau }}^{3}\,{{\propto }}\,{{{\sigma }}}^{3}\end{array}\right.$$
(2)
$${{\chi }}_{\perp }^{3{{\rm{\omega }}}}=\xi {{{\rm{\sigma }}}}^{3}+\eta {{\rm{\sigma }}}={{{\rm{\chi }}}}_{{skew scattering}}^{3{{\omega }}}\,+\,{{{\rm{\chi }}}}_{{side}-{jump}}^{3{{\omega }}}$$
(3)
Equations (5) and (6) show that skew scattering and side-jump contributions are \(\xi\) = 7.0 μm4·A−2 and \(\eta\) = −9.3 μm2·V−2. The ultrahigh conductivity of Fe5GeTe2 (σ ~ 104 S·cm−1 at 300 K) establishes skew scattering as the dominant mechanism underlying third-order nonlinear transport above 100 K. Higher temperatures weaken the QMD due to changes in the ordering of magnetic moments in domains. When the temperature rises above the Curie point, the ferromagnetic material loses its magnetism and becomes paramagnetic as the domains disintegrate, and the average magnetic moment becomes zero. The manifestation of QMD contributions becomes increasingly challenging to resolve experimentally as the temperature rises, where thermal fluctuations begin to dominate the nonlinear response characteristics.
Notably, the third-order signal appears to be minimally impacted by the scattering time at temperatures below 100 K, as shown in Fig. 4d (red curve), and exhibits a nonlinear relationship with σ2. An abrupt change in the correlation between \(\frac{| {E}_{\perp }^{3\omega }| }{{({E}_{\parallel }^{\omega })}^{3}}\) and σ2 is observed, contrasting significantly with the behavior arising from the Berry-connection polarizability tensor in TaIrTe410. According to the preceding analysis, it seems that QMD may have a substantial impact on the third-order nonlinear transport in Fe5GeTe2. To confirm the influence of the quantum metric, an examination of the \({\chi }_{\perp }^{3\omega }\) as a function of σ2 (depicted by the blue curve in Fig. 4e) is presented at temperatures ranging from 30 K to 100 K. By expanding the QMD formula21, we can deduce the scaling law:
$${\chi }_{\perp }^{3\omega }\,=\,{\eta }_{2}{{{\rm{\sigma }}}}^{2}+{\eta }_{0}$$
(4)
Similarly to Eq. (1−3), \({\eta }_{2}\) represent non-intrinsic Drude scattering, whereas \({\eta }_{0}\) signifies the normalized QMD in Eq. (4). By fitting the curve, it was determined that \({\eta }_{2}\) = 0.4 μm3·S−1·V−2 and \({\eta }_{0}\) = 7.1 μm·S·V−2, indicating that the contributions of QMD and Drude scattering to third-order nonlinear transport in 50 nm-Fe5GeTe2 sample are comparable in magnitude. Notably, comparable thickness samples (labeled #Device1, 40 nm thickness) exhibit analogous scaling behavior in third-order nonlinear response (Figure S19), further confirming the validity of our result. The magnetic state requirement for QMD generation is emphasized, while the intrinsic layer-dependent exchange interactions in Fe5GeTe2 induce thickness-enhanced ferromagnetic ordering, manifested by a rising Curie temperature with increasing sample thickness. To probe the competition between QMD contributions and scattering contributions at elevated temperatures, a sample with a thickness of over 100 nm (labeled #Device2), closer to a Curie temperature of 310 K, was tested (Figure S20). Experimental results suggest that the relationship between \({\chi }_{\perp }^{3\omega }\) and σ2 is expected to be linear within a temperature range of 1.6 K to 300 K, indicating that scattering dominates the nonlinear response. Thicker samples may lead to an increase in lattice disorder and impurities42,43 (Note S19), resulting in transverse asymmetric scattering due to effective spin-orbit coupling of electrons or impurities, which can account for this phenomenon. Moreover, non-intrinsic Drude scattering predominantly governs third-order transport, rendering the QMD contributions unobservable.
The nonlinear response in Fe5GeTe2 reveals a nuanced interplay between scattering dynamics and quantum geometric effects, where cooperative yet competing contributions from non-intrinsic Drude scattering and emergent QMD collectively govern the third-order transport characteristics. To highlight the robustness of the third-order signal in Fe5GeTe2, we compare its third-order conductivity (\({\chi }_{\perp }^{3\omega }\)) and third-order current conversion ratio (\(| {E}_{\perp }^{3\omega }| /{({E}_{\parallel }^{\omega })}^{3}\)) with those of previously reported materials10,23,24 and selected Hall devices fabricated in this work (Fig. 4f). Because of its unique electron spin properties, Fe5GeTe2 can function at room temperature. The material has a high third-order conductivity of 72 μm·S·V−2, nearly ten times greater than other materials. All device metrics surpass the highest reported values to date suggesting superior third-order current conversion efficiency. This makes Fe5GeTe2 a promising candidate for future room-temperature nonlinear devices in new quantum materials.