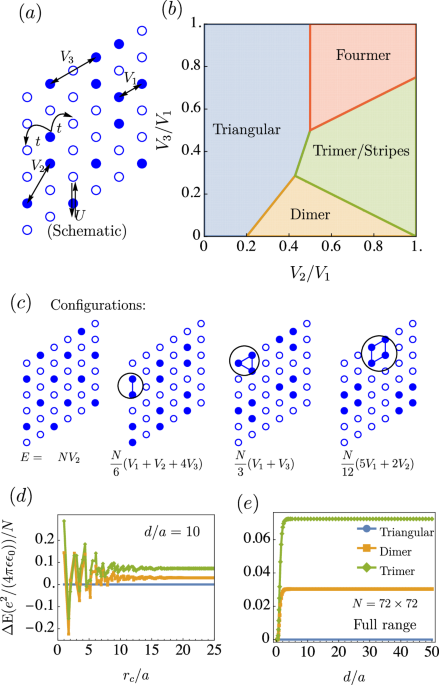
Classical phase diagram and competing charge-ordered states
To develop an intuition for the GWC problem, we first construct the classical ground state phase-competition diagram (t = 0 and U → ∞) for n = 1/3 of the Hamiltonian in Eq. (1) by exactly enumerating all states on a 6 × 6 lattice with periodic boundary conditions and picking the ground state(s). This calculation serves as a helpful starting point for further analyses, as the leading energy scale of the problem is the Coulomb interaction between electrons trapped in deep moiré potential wells14—a point to which we return later. We consider nearest (NN, strength V1 = 1), next-nearest (NNN, strength V2) and next-to-next nearest neighbor interactions (NNNN, strength V3); our results are summarized in Fig. 1b, c. No double occupancy is allowed, i.e., U → ∞, and spin is irrelevant. The n = 2/3 results can be obtained by swapping the roles of particles and holes. (For systems larger than 6 × 6, we have carried out additional low temperature classical Monte Carlo calculations to navigate the low energy landscape. We have observed the existence of regions of phase space where the configurations reported in Fig. 1b, c do not strictly correspond to the true ground state, just low energy states.)
For small V2, V3 the \(\sqrt{3}\times \sqrt{3}\) triangular GWC is stable, as the total charge configuration completely avoids the V1 and V3 costs at the expense of a V2 cost. However, other phases are favored for modest V2/V1 and V3/V1. For example, for V3 = 0, 0.2 ≤ V2/V1 ≤ 1 stabilizes a “dimer” crystal, the state that arises out of a compromise – the system pays some V1, V2 and V3 costs by pairing up into dimers, as shown in Fig. 1c. Interestingly, on the 6 × 6 torus, this arrangement is found to be degenerate with 3707 other states (degeneracies include those beyond those arising from translation and different orientations of the dimer crystal) suggesting a high amount of “charge frustration”. This degeneracy persists for V3 = 0 for all V2/V1 as long as the system is in the dimer phase. (On larger system sizes, we observe a finite residual entropy per site from integration of the specific heat from classical Monte Carlo, suggesting this number is exponential with system size). On adding small, but finite, V3 > 0, the dimer (and symmetry related states) are favored, and this large degeneracy is lifted.
At much larger V3, a crystal is formed out of a cluster of three charges, which we refer to as a “trimer”. This state pays no V2 cost but pays some V3 costs between trimers. It is exactly degenerate with a period-3 “stripe” state, a periodic arrangement of one-dimensional lines of charges. In the case of this state, which will feature in Fig. 2, all V1 and V3 costs are paid within each one-dimensional stripe. (On larger sizes we have observed the existence of lower energy amorphous states, featuring short stripes and trimers.) Then, when V2 and V3 are both large, a “fourmer” crystal, shown in Fig. 1c, is stabilized. In general, we note that at low density the system avoids energy penalties by clustering particles, even in the absence of any attractive interactions—reminiscent of a pairing mechanism discussed in ref. 41 and recent reports of “bubble phases” in Landau levels42.
Fig. 2: Charge ordered quantum phases for a series of extended Hubbard models.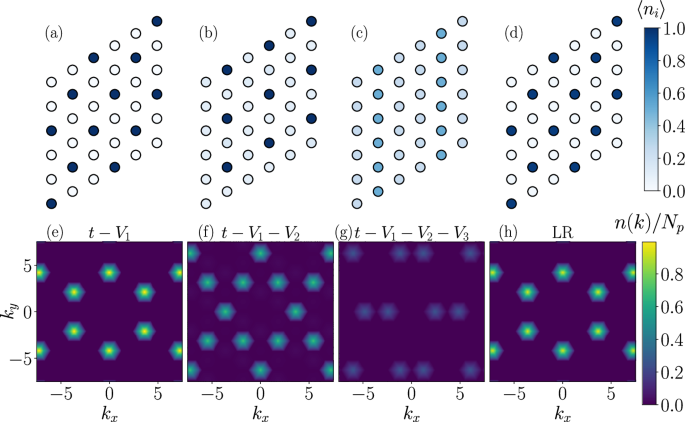
(a–d) show the expectation value of the local charge density 〈ni〉 on every site i of a 6 × 6 torus for n = 1/3, computed in the quantum ground state (obtained from DMRG) for a series of models. These models were obtained by truncating the LR model (model 3 in Table 1) to various ranges (a) model 4 but with V2 = V3 = 0 (b) model 4 with V3 = 0 (c) model 4 (d) model 3. The y axis is vertical and the x axis is horizontal. (e–h) show the corresponding absolute value of the Fourier transform of the charge distribution in momentum space; \(n(\overrightarrow{k})\) is defined as \(\left\vert \right.\sum _{i}\left(\langle {n}_{i}\rangle -\frac{1}{3}\right){e}^{i{\bf{k}}\cdot {{\bf{r}}}_{{\bf{i}}}}\left\vert \right.\) and Np is the number of particles (i.e. N/3). The DMRG simulations utilized a maximum bond dimension of up to 10000 and were carried out in the Sz = 0 sector.
We now ask where in the phase-competition diagram of Fig. 1b are typical moiré TMD materials expected to be. To answer that question, it is necessary to compute the extended Vij Hubbard parameters. Following ref. 6, we consider a double-gate screened Coulomb interaction
$$V(\overrightarrow{r})=\frac{{e}^{2}}{4\pi \epsilon {\epsilon }_{0}a}\mathop{\sum }\limits_{k = -\infty }^{k = \infty }\frac{{(-1)}^{k}}{\sqrt{{\left(\frac{kd}{a}\right)}^{2}+{\left(\frac{| \overrightarrow{r}| }{a}\right)}^{2}}},$$
(2)
where a is the moiré lattice constant, d is the separation between gates, ϵ is the dimensionless dielectric constant, ϵ0 is the vacuum permittivity, and \(\overrightarrow{r}\) refers to the vector connecting the two moiré lattice sites. The above form of the Coulomb interaction assumes two gates symmetrically located (above and below) at a distance d/2 from the moiré system, as relevant for the experiment of ref. 6, however our conclusions should generalize, with appropriate quantitative modifications, to other gate configurations7. In the above calculation of \({V}_{ij}\equiv V({\overrightarrow{r}}_{i}-{\overrightarrow{r}}_{j})\) parameters, we also assume that the Wannier functions are localized on a length scale much smaller than the moiré lattice constant (which is expected for this topologically trivial system14,28). In such a case it is reasonable to approximate the interactions as those between point charges—we employ this approximation throughout this work. We clarify that, in principle, the Wannier function overlap can be incorporated (e.g. see ref. 13,14,25) into estimating the on-site Hubbard U and extended Vij. While this treatment is expected to only provide a small correction to the extended Vij parameters, it is essential for the estimation of the Hubbard U e.g., as discussed in ref. 36. However, since our work focuses on fillings away from one electron per moiré cell, our results are not significantly influenced by the precise value of U- all that is important for our conclusions is that U is large enough to prevent any appreciable double occupancy on a site.
As is explained in Supplementary Note 1, we treat the LR nature of the interaction by tiling the finite size cluster (the fundamental unit cell) multiple times to cover all of space, and then use the arrangement to calculate the effective interaction between any two sites (including the site with itself) in the fundamental unit cell. This effective Hamiltonian is simulated with classical and quantum methods. We note that the exponential decay of the potential with distance guarantees rapid convergence of the procedure with increasing the number of tiles. We also clarify that these effective interactions must not be confused with the renormalization of the NN interaction due to the LR tails that we discuss later in the paper.
To highlight how the competition between ground states is sensitive to the range of truncation, we consider a sequence of models with increasing range rc (the distance at which the interaction is truncated) i.e., increasing number of non-zero Vij extended Hubbard model terms in Eq. (1). Specifically, we take \(V(\overrightarrow{r})\) to have the form in Eq.(2) for \(r\equiv | \overrightarrow{r}| \le {r}_{c}\) and \(V(\overrightarrow{r})=0\) for r > rc. In Fig. 1d, we plot, for d/a = 10, the energy difference (per site) of each of the competing states we found in Fig. 1b with respect to the energy of the triangular crystal. For NN interactions, indeed, the triangular \(\sqrt{3}\times \sqrt{3}\) crystal is the ground state, however, truncating to NNN yields the dimer crystal and truncating to higher neighbor interactions generically gives more complex ground states. Figure 1e shows the competition between ground states for the LR interaction (i.e., rc→∞) as a function of d/a. When the LR interaction is considered, we find that the \(\sqrt{3}\times \sqrt{3}\) GWC is always the ground state for any gate distance d/a ≳ 1.
Quantum treatment, “pinball phase”, and state selection
The small energy differences between competing classical states, particularly when the interactions are long-ranged, as in Fig. 1d, highlight the need to account for quantum effects accurately. To do so, we consider the simplest possible kinetic term, the NN hopping, which was estimated to be much larger than other hoppings (see Table 1). In principle, in analogy to the Vij Hubbard terms in Eq. (1), the kinetic term could have contributions beyond NN hopping. However, since kinetic energy is significantly suppressed in GWCs and largely acts as a perturbation to ground states selected by the Coulomb interactions, we argue that it is sufficient to consider just the dominant NN term to capture the relevant charge physics we discuss in this work. In future work, it would be interesting to study the role of extended hoppings, especially in parts of the phase diagram where multiple charge or magnetic orders compete closely13,36.
Table 1 Summary of parameter sets employed in this work, which we refer to as models 1–4
We obtain the quantum mechanical ground state on finite clusters using matrix product state (MPS) based DMRG calculations43,44. We work with fixed particle number and total Sz = 0. On a given system size, DMRG is limited only by finite bond dimension, when this is inadequate DMRG favors low entanglement states such as those with broken translational symmetry. Given the 1-D nature of the MPS which is used to “snake through” a 2-D system, the accuracy of DMRG is typically limited on systems with periodic boundaries (torus in 2D) or those with long correlation lengths45. On the other hand, the torus geometry has the advantage of having no boundary effects and so is possibly more representative of the thermodynamic limit. Thus we interpret the results of our bond dimension-limited runs on tori, that favor symmetry-broken states with low entanglement, to be genuinely representative of the underlying physics, despite them not being exact eigenstates. To supplement these results and build confidence in our results, we have carried out additional DMRG calculations on cylinders. The quasi-1D nature of the cylinders, while conducive for DMRG, is known to affect the physics especially if the length of the cylinder is taken to be much larger than its width46. Despite these caveats, we arrive at similar qualitative conclusions on cylinders, see additional results and discussion in Supplementary Note 2.
The representative results for n = 1/3 for a sequence of FR and LR Hubbard models on a 6 × 6 torus (computed with a maximum bond dimension of 10000) are shown in Fig. 2a–d. All the finite-range models discussed in this section are obtained by combining the parameters from ref. 6 and ref. 36 (i.e. model 3 with ϵ = 3.9 and d/a = 10, see Table 1) and then setting all Vij beyond a certain range to zero. (Note that when model 3 is truncated to V1, V2, V3 it yields model 4.) We plot the charge density (〈ni〉) on every lattice site and also show the Fourier transform of the density correlation function, Fig. 2e–h. As expected, we find that for the NN model (V1/t = 22.1) the \(\sqrt{3}\times \sqrt{3}\) triangular crystal seen classically is stable to the introduction of a hopping i.e. quantum effects, see Fig. 2a. The charge density is sharply localized on the sites of the \(\sqrt{3}\times \sqrt{3}\) crystal, c.f. Fourier transform in Fig. 2e, confirming the identification of this charge density wave ground state with that of a GWC.
However, the ground state of the NNN model (t−V1−V2 model, i.e. model 4 with V3 = 0) is strikingly distinct from the classical expectation—we find no evidence of stabilization of a dimer crystal or any of the other classically degenerate ground states. Instead, we see the appearance of charge centers (with 〈ni〉 ≈ 1) at sites of a triangular crystal with a spacing of two (moiré) lattice constants, Fig. 2b, f. This emergent 2 × 2 triangular crystal accounts only for 1/4 filling, and the remaining 1/3−1/4 = 1/12 charge density was found to be delocalized on the other sites. This “partially melted” GWC arises out of a compromise – the system avoids paying both V1 and V2 costs between the charges on the “pinned” sites and also benefits from kinetic energy delocalization of the remaining charges. There is also a Coulomb energy cost associated with the delocalized charges interacting with the pinned charges, but overall, the first two effects dominate, leading to the stabilization of such a crystal. We envisage that while this NNN model does not govern the realistic moiré TMD system, the phase we have found here could be potentially realized in other platforms such as cold atoms23,47. We also note that previous theoretical work established a “pinball liquid phase”48,49 at a different density n = 1/2 (quarter filling) and in an extended Hubbard model on the triangular lattice with only V1 interactions i.e. V2 = 0. For n = 1/2 the pins are arranged on a \(\sqrt{3}\times \sqrt{3}\) triangular crystal (in contrast to the 2 × 2 cell seen here), but the essential physics of coexisting insulating and delocalized degrees of freedom appears to be similar.
The NNNN model (t − V1 − V2 − V3 model for the parameter set in Table 1 i.e. model 4) yields a period-3 stripe ground state, resembling its classical counterpart—see Fig. 2c. Here, one of three equivalent directions of the triangular lattice is spontaneously selected. Unlike the classical result, however, charge localization is weakened in strength due to quantum effects, leading to smaller peaks in the Fourier transform of the charge density profile, see Fig. 2g. It is interesting to observe that extended stripes are favored over local trimers—a possible mechanism is “order by disorder” which dictates how quantum state selection occurs among a collection of classically degenerate states50,51 and which has also been shown to be relevant for other materials with charge order52.
Most importantly, we find that the LR model (i.e. model 3) stabilizes a \(\sqrt{3}\times \sqrt{3}\) triangular GWC, see Fig. 2d. The resulting charge density localization is identical to the NN model, with only minor quantitative differences in the densities on the GWC sites, c.f. Fig. 2e, h. This result suggests that the NN model, with appropriate renormalization of the extended interaction V1, may capture the essential physics of GWC melting at finite temperature, which we will explore next.
Finite temperature properties of GWC
We now proceed to analyze the finite temperature properties of the GWCs. We begin by considering the classical case first (t = 0, U → ∞ in Eq.(1)). Figure 3a shows the specific heat per site Cv/N as a function of temperature for the LR and truncated NN classical models for the case of d/a = 10 i.e. model 2, and model 2 with only V1 ≠ 0, respectively. Calculations were done with classical Metropolis Monte Carlo for n = 1/3 for a range of system sizes; the n = 2/3 results are identical due to particle-hole symmetry. While finite size effects are naturally expected, we observe that the location of Tc for system sizes as small as N = 27 sites is broadly consistent with much larger sizes (to within 10%). Importantly, we find that despite both models having the same classical ground state, the charge ordering temperature Tc of the LR model is a factor of ≈ 3.6 smaller than that of the NN model; indicating that the long-range tail significantly renormalizes the NN interaction. We will revisit this finding soon and also provide an explanation for it.
Fig. 3: Specific heat per site (Cv/N) as a function of temperature (T), for various models considered in this work.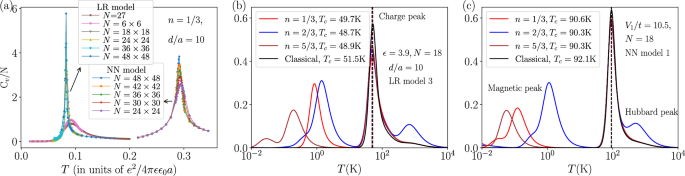
a Cv(T)/N for the LR model (model 2 in Table 1) and the NN model (model 2 but truncated to have only V1 non-zero) computed with classical Metropolis Monte Carlo for multiple system sizes. The classical model with t = 0, U → ∞ is particle-hole symmetric, so the results for n = 1/3 and n = 2/3 are identical. (b, c) show Cv(T)/N for the quantum models obtained from exact diagonalization for N = 18 sites (see Supplementary Note 3) for three densities n = 1/3, 2/3 and 5/3. (b) Cv(T)/N for the LR quantum model (model 3) and (c) Cv(T)/N for a NN (model 1). Additionally, in panels (b) and (c) we show the “classical” result for n = 1/3 for the same system size, obtained by setting t = 0 but not changing the other parameters (i.e. keeping U large, but finite).
With an expectation of the classical melting behavior in place, we now consider a quantum mechanical finite-temperature study of the Hamiltonian in Eq. (1), specifically for model 1 and 3 in Table 1, using ED (full diagonalization) and the finite temperature Lanczos method (FTLM)53,54, see the Methods section. Since spin has an important role to play in the quantum simulations, we have also shown results for the n = 5/3 case; this density is a spinful particle-hole partner of the n = 1/3 case, its Hamiltonian is equivalent to that of n = 1/3, but with t → − t.
Given that meaningful conclusions and trends can be drawn from small clusters, we compute the quantum mechanical specific heat for the N = 18 system (see Supplementary Note 3 for cluster shape and symmetries used and Supplementary Note 4 for simulations on more sizes). We also consider (using the same ED procedure) the “classical” case with t = 0 but with otherwise identical parameters, i.e., U large but finite. Our results are shown in Fig. 3b, c on a log temperature scale for the LR (model 3) and NN (model 1) case, respectively. The NN interaction strength in model 1 is in the ballpark of that studied in ref. 36 where ϵ was chosen to be 10.
The differences in the choices of ϵ (see for example work of ref. 6 and ref. 36) followed by truncation (or lack of it) can potentially reconcile parameter sets that otherwise look very different. In particular, two effects compete with one another: increasing ϵ has the effect of decreasing the overall strength of Coulomb interactions and hence lowering the ordering temperature, and truncating the LR interaction eliminates the overall renormalization that comes from the LR tail, in turn increasing the ordering temperature. The end result is that the effective V1/t used in the NN model is approximately 10.536. We find that this, in turn, results in the GWC temperature melting temperature that is a factor of roughly two higher (see Fig. 3c) than that measured in experiment and reproduced by classical Monte Carlo with the full LR model with ϵ = 3.96.
The quantum-mechanical finite-temperature simulations show that the entropy is released in multiple steps for both LR and NN models. For example, for n = 2/3 there are at least three prominent and distinct temperature scales associated with either a crossover or transition. The highest scale is associated with the large Hubbard U, as has been noted previously in ref. 19 in the context of the on-site Hubbard model. The intermediate scale corresponds to the melting of the charge order and has been accessed experimentally6. The low-temperature bump (crossover) corresponds to the destruction of finite-range magnetic correlations (there is no true long order at finite temperature due to the Mermin-Wagner theorem55). For n = 1/3 and n = 5/3, the Hubbard feature, while present, is greatly suppressed. The charge ordering scales are similar, but not exactly the same, and the magnetic scales are different from one another and the n = 2/3 case. As magnetic correlations are quantum mechanical in nature, they are completely absent in the classical calculations. (We also note the presence of an additional ultra-low temperature feature which is expected to emerge from small but finite size gaps, and hence we ignore its presence for the discussion here).
The suppression of kinetic energy in the GWC means that its melting is essentially, but not completely, classical in origin. This is true for both the NN and LR models. For the NN model with V1/t = 10.5 (model 1), we find a small difference (within ≈ 0.3 K) in the locations of Tc for n = 1/3, 2/3 and 5/3, and an approximately 2 K difference with the “classical” case where n = 1/3 and t = 0, while all other parameters were kept fixed (i.e. U was kept finite). We attribute these observations to the small amount of quantum melting of the ground states and the kinetic energy term on the triangular lattice breaking the particle-hole symmetry of the t = 0 model. The LR model (model 3) has effectively weaker NN interactions which results in a lower Tc. Importantly, for this model the difference between the n = 1/3 and 2/3 cases is bigger i.e. approximately 1 K, which is in the ballpark of the experimental findings6.
As mentioned previously, the difference between n = 1/3, 2/3, 5/3 manifests itself even more prominently in the low-temperature magnetic features, which remain to be experimentally explored, c.f. Fig. 3b. Our calculations predict the magnetic crossover temperatures in the range approximately 0.2–1 K. These magnetic crossover scales are potentially within an experimentally realizable range, suggesting that future experiments sensitive to spin texture (e.g., NV center scanning techniques, spin-polarized scanning tunneling microscopy or nanoSQUID) could resolve the nature of the various spin ground states13,16,37,38,39,40.
Predictions for quantum and thermal melting of GWC
We now study the possible quantum mechanical melting of the GWC charge order by controlling the screening environment by tuning d/a. Smaller d corresponds to stronger screening, manifesting in a shorter length scale over which the LR Coulomb interaction becomes suppressed by the gate. This suppression of the effective LR Coulomb interaction range with decreasing d/a should eventually drive the system to metallicity despite U being large because of the low density of particles or holes. This is quantitatively established in Fig. 4a, which shows the value of the order parameter computed on the N = 27 site cluster (see Supplementary Note 3) from ED using the Lanczos method for both n = 1/3 and 2/3. (The order parameter corresponds to the Fourier component of the density-density correlation function at the K points.) At large d/a, its value is approximately constant, in contrast, on lowering d/a, its value rapidly decreases for d/a ≲ 1. We note in passing that given that a ≈ 8 nm, achieving ratio d/a ≲ 1 is within experimental range of the hBN dielectric thicknesses56,57.
Fig. 4: Dependence of effective ground state and finite temperature properties of GWCs on gate distance.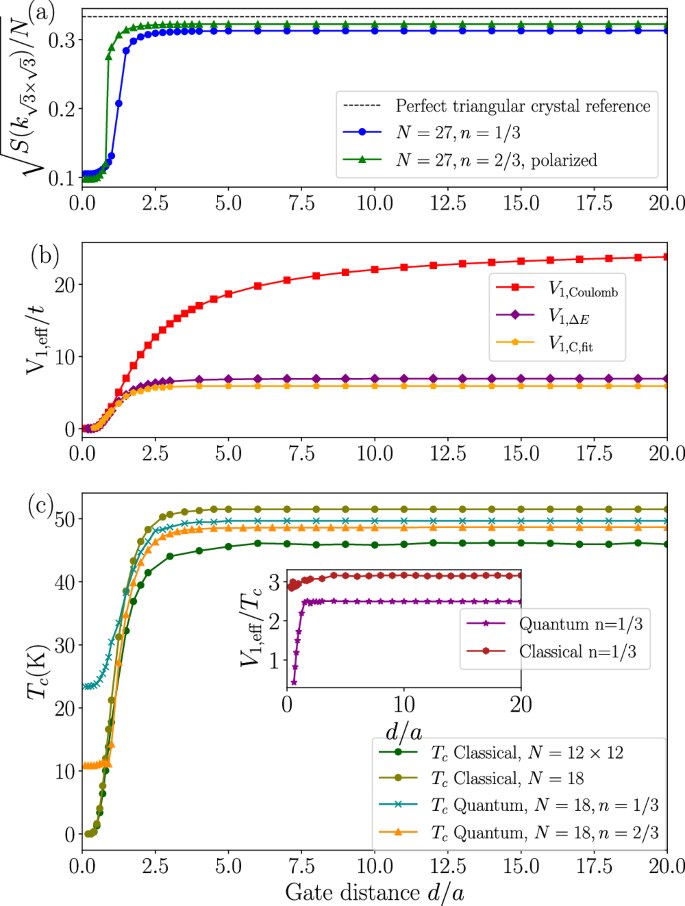
a Order parameter (defined in terms of the charge structure factor, \(S({\bf{k}})\equiv \frac{1}{N}\sum _{i,j}\langle {n}_{i}{n}_{j}\rangle {e}^{i{\bf{k}}\cdot ({{\bf{r}}}_{i}-{{\bf{r}}}_{j})}\) computed at a representative momentum point \({k}_{\sqrt{3}\times \sqrt{3}}\) that shows a peak for the \(\sqrt{3}\times \sqrt{3}\) triangular charge order) in the quantum ground state, as a function of d/a. Calculations were carried out in the momentum (0,0) sector for N = 27 and n = 1/3 (in the Sz = 1/2 sector) and n = 2/3 (in the maximally polarized Sz sector). The parameters correspond to model 3 (Table 1) for variable d/a. The dotted line represents the reference value for a perfect \(\sqrt{3}\times \sqrt{3}\) triangular charge order. b Effective NN V1,eff/t interaction as a function of d/a obtained from: the bare interaction potential (V1,Coulomb ≡ V(r = a), see Eq. (2)), one defect energy (V1,ΔE), and from fitting the specific heat curve of the LR model (model 3 with variable d) and NN model (V1,C,fit). c The critical temperature Tc corresponds to charge order melting transition for three cases: classical, quantum n = 1/3, and n = 2/3, as a function of d/a. (Inset) Ratio of the V1,eff to Tc using V1,ΔE (classical) and V1,C,fit (quantum) from (b).
The dependence of the screened Coulomb interaction from Eq. (2) as a function of d/a does not immediately reveal why the order parameter should be essentially constant for large d/a. For example, V1 grows (albeit slowly) with increasing d/a, see Fig. 4b (red, V1,Coulomb curve), and the tail decays rapidly with decreasing d/a, see Supplementary Note 1. We propose that the origin of the relative independence of the order parameter with d/a stems from the “cancellations” of the LR tail which yield an effective NN strength. This NN strength is much smaller than V1,Coulomb, confirming the expectation we had from the classical specific heat analysis.
We verify this hypothesis in two complementary ways, as shown in Fig. 4b. First, at the purely classical level in the LR model (model 2 but with variable d), we calculate the energy to create a “defect”, by moving one charge in the triangular GWC to a neighboring unoccupied site of the triangular lattice. Both the GWC and representative defect configuration are shown in Fig. 5. For a given d/a, the energy difference between the two configurations was computed and defined to be 2V1,ΔE – this is the energy cost of a defect in the effective NN model. V1,ΔE/t is found to be roughly 6.9 and is essentially independent of d/a (purple curve in Fig. 4b). Figure 5 also graphically depicts the Coulomb energy contributions associated with both configurations. The corresponding expression suggests that their subtraction leads to effective cancellations of the long range tail. It is this cancellation that leads to an energy difference that is (almost) independent of d/a.
Fig. 5: Schematic of energetic contributions arising from a single defect in the triangular GWC.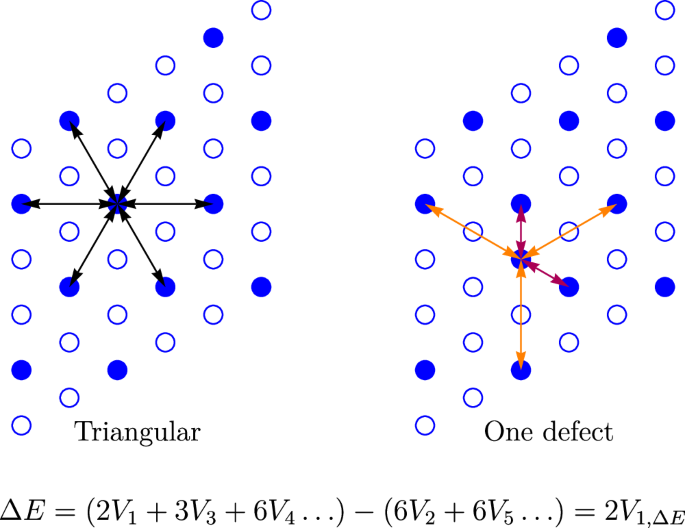
The left panel shows the \(\sqrt{3}\times \sqrt{3}\) triangular GWC and the underlying original moiré triangular lattice. The right panel corresponds to the configuration where a single charge in this GWC is moved to a vacant nearest neighbor site, creating a “defect” in the GWC. In both cases some (not all) of the non-zero contributions to the Coulomb energy are highlighted, the expression shown corresponds to the energy difference between the two configurations, which is thus the energy of a single defect 2V1,ΔE in the effective nearest neighbor model. Vn corresponds to the potential energy arising from the nth nearest neighbors.
In the second method, we vary V1 in the NN model such that its specific heat profile most closely matches that of the LR quantum model. We refer to this optimal value of V1 as V1,C,fit. For this purpose, we define a cost function (see Supplementary Note 5), and we find that this procedure reproduces well both the magnetic bump and charge peak. We find that this value is in the same ballpark, V1,C,fit/t ≈ 5.9, and importantly, it is essentially independent of d/a confirming our hypothesis (orange curve in Fig 4b). We collectively refer to both these values as V1,eff with the understanding that it refers to V1,ΔE in the classical case and V1,C,fit in the quantum case. We note that both these values of V1,eff/t place the material on the insulating side of the metal-insulator transition (MIT) for n = 1/3 (VMIT/t ≈ 458), but this value of V1,eff/t is considerably lower than what has been reported for these moiré materials (e.g. ref. 36). The transition between metal to insulator is also expected to be first order58. This closeness to a phase boundary suggests that local disorder may stabilize pockets of insulating (charge-ordered) and metallic regions. We conjecture that this proximity to the MIT transition potentially lies at the origins of the real-space signal variation of what should be a pristine \(\sqrt{3}\times \sqrt{3}\) GWC in the STM maps of ref. 7.
The impact of the renormalization of the NN interaction is also confirmed by plotting the Tc of the classical and quantum models as a function of d/a in Fig. 4c. As expected, Tc follows V1,eff from either method rather than V1,Coulomb, which we also check by plotting the ratio of V1,eff/Tc in the inset. (We remark that similar observations for Tc were made for specific values of d/a for the classical model in ref. 6, but the origin of this effect was not explained.) Based on our calculations we predict that Tc must not change appreciably for large d/a but at and below d/a ≈ 1 − 2 the GWC becomes unstable and melts to give a Fermi liquid.
Magnetic interactions of GWC for n = 1/3
We conclude by addressing briefly the question of magnetism of GWCs in the moiré TMDs, which remains an active area of research. We present some estimates of the GWC melting (crossover) temperature (which we refer to as Tm) for n = 1/3 as a function of V1/t in the NN model. Strictly speaking, there is no true long-range magnetic order in two dimensions at finite temperature, so there is no sharp peak in the specific heat at low temperature, and we associate Tm with the location of the local maximum.
For V1/t large (and assuming U ≫ V1), where the charge order corresponds to the \(\sqrt{3}\times \sqrt{3}\) triangular crystal, the magnetic exchange between two particles with opposite spins is generated (to lowest order) by an exchange process that involves four hops (two hops for each particle) on the underlying triangular lattice, shown in Fig. 6b. This gives rise to a magnetic exchange scale that is expected to scale as \({t}^{4}/{V}_{1}^{3}\). We see evidence of this scale indirectly in Tm which scales as the same power of V1 (see Fig. 6a). We plot physical estimates for Tm in Kelvin, incorporating the overall scale factor coming from t, which clarifies what temperatures should be probed in future experiments. More work is needed to ascertain detailed properties in the context of LR interactions and beyond NN hoppings, along with higher order spin exchange effects.
Fig. 6: Magnetism in the triangular GWC at n = 1/3.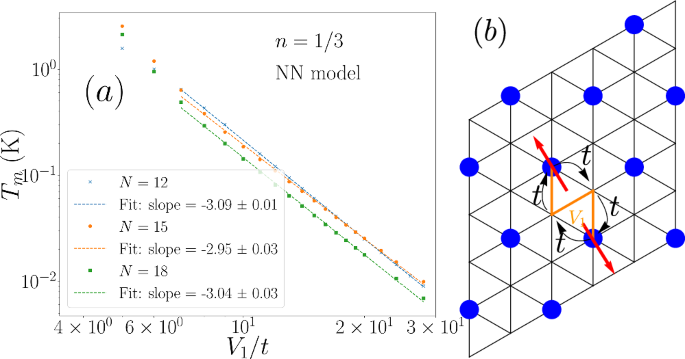
a Magnetic crossover scale Tm as a function of NN interaction V1/t on a log-log scale for three system sizes N = 12, 15, 18 for n = 1/3. The overall factor of t = 1.81 meV is incorporated in Tm to connect to physical temperature scales. The straight line fit, biased towards larger V1/t, shows the approximate \({V}_{1}^{-3}\) dependence. b A schematic for the exchange process of two particles with opposite spin involving four hops, that gives rise to the effective magnetic interaction. The orange solid lines show the NN interaction V1 which occurs during the hopping process.