Our goal in this part is to get the next form of solutions for Eq. (1):
$$\begin{aligned} R(x,y,z,t)=R(\xi ) e^{i(\omega ~t-\nu _1~ x-\nu _2~ y-\nu _3~ z+\theta )},~ \xi =\eta _1~x+\eta _2~y+\eta _3~z-\gamma ~t, \end{aligned}$$
(7)
in which \(\gamma\) denotes the velocity of the solitonn along the x, y, and z axes, while the wave numbers are symbolized by \(\nu _1\), \(\nu _2\), and \(\nu _3\). Additionally, \(\theta\) stands for phase constant, and \(\omega\) represents the soliton frequency. Substituting by Eq. (7) into Eq. (1) then separating into real and imaginary parts, we have:
The real component:
$$\begin{aligned} & s_1~ R(\xi )^{1-n}+s_2~ R(\xi )^{1-2n}+s_3~ R(\xi )^{1-3n} +s_4~ R(\xi )^{1-4n}+w_1~ R(\xi )^{1+n}+w_2~ R(\xi )^{1+2n}+w_3~ R(\xi )^{1+3n}\nonumber \\ & \quad +w_4~ R(\xi )^{1+4n}+(-\omega +m_1~ \nu _1^2+2m_4~ \nu _1 ~ \nu _2-2m_6~\nu _3~\nu _2+m_2~ \nu _2^2-2m_5~\nu _3~\nu _1+m_3~ \nu _3^2)~R(\xi )\nonumber \\ & \quad -R”(\xi )~(m_1~ \eta _1^2+2m_4~ \eta _1~\eta _2-2m_6~\eta _3~\eta _2+m_2~\eta _2^2-2m_5~\eta _1~\eta _3 +m_3~\eta _3^2)=0. \end{aligned}$$
(8)
The imaginary component:
$$\begin{aligned} & \gamma -2m_1~\nu _1~\eta _1+2m_6~\nu _2~\eta _3+2m_5~\nu _3~\eta _1+2m_6~\nu _1~\eta _2-2m_2~\nu _2~\eta _2\nonumber \\ & \quad -2m_4~(\nu _2~\eta _1+\nu _1~\eta _2)+2m_5~\nu _1~\eta _3-2m_3~\nu _3~\eta _3=0. \end{aligned}$$
(9)
Equalizing the coefficient of Eq. (9) to zero provides
$$\begin{aligned} \gamma =2\eta ~(m_1~\nu _1+m_4~\nu _2-m_5~\nu _3)+2\eta _2~(-m_6~\nu _1+m_2~\nu _2+m_4~\nu _2)+2\eta _3~(m_3~\nu _3-m_5~\nu _1-m_6~\nu _2). \end{aligned}$$
(10)
To implement the IMETF scheme on the real portion, the balance principle has to applied to get the integer k, by comparing the highest-order linear derivative term with the leading-order nonlinear term.
According to Eq. (9), the chain rule applied to the function \(R(\xi ) = \sum _{i=-N}^{N} \alpha _{i} W(\xi )^{i}\) results in terms with dominant behavior of order \(\mathbf {W^{N+2}}\) from the second derivative \(R”\). Conversely, terms of leading order \(\mathbf {W^{2N}}\) are produced by the nonlinear term \(\mathbf {R^{1+4n}}\).
By equating the dominant powers of \(W(\xi )\) in both terms, we get:
$$\begin{aligned} k+2=(1+4n)~k\quad \implies \quad k=\frac{1}{2n}. \end{aligned}$$
, so the following transformation can be applied on the real part to get an integer value for k:
$$\begin{aligned} R(\xi ) =U(\xi )^{\frac{1}{2n}}. \end{aligned}$$
(11)
Eq. (8) becomes:
$$\begin{aligned} & 4n^2~s_4+4n^2~s_2~U(\xi )+4n^2~(\Pi _2-\omega )~U(\xi )^2+4n^2~w_2~U(\xi )^3+4n^2~w_4~U(\xi )^4+(1-2n)~\Pi _1~U'(\xi )^2\nonumber \\ & \quad +2n~\Pi _1~U”(\xi )~U(\xi )=0, \end{aligned}$$
(12)
Where
$$\begin{aligned} & \Pi _1=-(m_1~\eta _1^2+2m_4~\eta _1~\eta _2+m_2~\eta _2^2-2m_5~\eta _1~\eta _3-2m_6~\eta _2~\eta _3+m_3~\eta _3^2), \end{aligned}$$
(13)
$$\begin{aligned} & \Pi _2= m_1~\nu _1^2+2m_4~\nu _1~\nu _2+m_2~\nu _2^2-2m_5~\nu _1~\nu _3-2m_6~\nu _2~\nu _3+m_3~\nu _3^2. \end{aligned}$$
(14)
Balancing \(U(\xi )^4\) with \(U”(\xi )~U(\xi )\), we get \(k=1\) by the balancing procedure that was previously mentioned, \(4k=k+2+k\). According to the proposed approach, the solution of Eq.(12) will be declared into the next form
$$\begin{aligned} U(\xi )=h_0+h_1 \rho (\xi )+j_1 \rho (\xi )^{-1}. \end{aligned}$$
(15)
Substituting by Eq. (15) and its Riccati equation Eq. (6) into Eq. (12) then equating all the coefficients of \(\rho ^i\) to zero, a system of non-linear equations will be resulted that can be resolved using mathematica packages. The results will be as follow:
Case 1. \(q_0=q_1=q_3=0\)
Result(1)
$$q_2=\frac{q_4~(\omega +2n~\omega +6w_4~h_0^2-\Pi _2 -2n\Pi _2 )}{w_4~h_1^2},~ q_4=\frac{-4n^2~w_4~h_1^2}{(1+2n)\Pi _1},~ j_1=0, ~h_0 =\frac{-(1+2n)w_2}{4(1+n)w_4},$$
$${-22em} s_2=\frac{2(-1+n)~w_4~h_0~(2q_4~h_0^2+q_2~h_1^2)}{(1+2n)~q_4}.$$
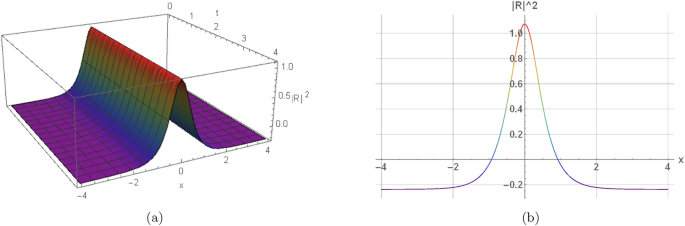
The next bright soliton solution can then be elevated
$$\begin{aligned} R(x,y,z,t)= & \left[ -\frac{(1+2n)w_2}{4(1+n)w_4}+\sqrt{\frac{\frac{3(1+2n)^2~w_2^2}{8(1+n)^2~w_4}+(1+2n)(\omega -\Pi _2)}{w_4}}\right. \nonumber \\ & \left. \quad \operatorname {sech}\left( 2(\eta _1~x+\eta _2~y+\eta _3~z-\gamma ~t) \sqrt{\frac{n^2\left( \frac{3(1+2n)^2~w_2^2}{8(1+n)^2~w_4}+(1+2n)(\omega -\Pi _2)\right) }{(1+2n)~\Pi _1}}\right) \right] ^{\frac{1}{2n}}\nonumber \\ & \times e^{i(t \omega +\theta -\nu _1 x-\nu _2 y-\nu _3 z)} \nonumber \\ & ,{\frac{\frac{3(1+2n)^2~w_2^2}{8(1+n)^2~w_4}+(1+2n)(\omega -\Pi _2)}{w_4}>0,~ \frac{n^2\left( \frac{3(1+2n)^2~w_2^2}{8(1+n)^2~w_4}+(1+2n)(\omega -\Pi _2)\right) }{(1+2n)~\Pi _1}>0.} \end{aligned}$$
(16)
The next singular periodic solution can then be elevated
$$\begin{aligned} R(x,y,z,t)= & \left[ \frac{-(1+2n)~w_2}{4(1+n)~w_4}+\sqrt{\frac{\frac{3(1+2n)^2~w_2^2}{8(1+n)^2~w_4}+(1+2n)(\omega -\Pi _2)}{w_4}}\right. \nonumber \\ & \left. \times \sec \left( (\eta _1~x+\eta _2~y+\eta _3~z-\gamma ~t)~\sqrt{\frac{-n^2\left( \frac{3(1+2n)^2~w_2^2}{8(1+n)^2~w_4} +(1+2n)(\omega -\Pi _2)\right) }{(1+2n)~\Pi _1}}\right) \right] ^{\frac{1}{2n}}\nonumber \\ & \times e^{i(t \omega +\theta -\nu _1~ x-\nu _2~y-\nu _3~z)},\nonumber \\ & {\frac{\frac{3(1+2n)^2~w_2^2}{8(1+n)^2~w_4}+(1+2n)(\omega -\Pi _2)}{w_4}>0,~\frac{n^2 \left( \frac{3(1+2n)^2~w_2^2}{8(1+n)^2~w_4}+(1+2n)(\omega -\Pi _2)\right) }{(1+2n)~\Pi _1}
(17)
Case 2. \(q_1=q_3=0\)
Result(1)
$$h_1=0,~h_0=\frac{-(1+2n)~w_2}{4~(1+n)~w_4},~q_2=\frac{n^2~((-1+n)~(1+2n)^2~w_2^3+16~(1+n)^3~s_2~w_4^2)}{2~(1+n)^2~(-1-n+2~n^2)~w_2~w_4~\Pi _1},~q_4=\frac{-(1+2n)~q_2^2~\Pi _1}{16~n^2~w_4~j_1^2}.$$
The next singular soliton is then elevated
$$\begin{aligned} R(x,y,z,t)= & \frac{1}{4}\left[ -\frac{(1+2n)w_2}{(1+n)w_4}\right. \nonumber \\ & \left. + \frac{\coth \left( \frac{1}{2}(\eta _1 x+\eta _2 y+\eta _3 z-\gamma t)\sqrt{-\frac{n^2((-1+n)(1+2n)^2w_2^3+16(1+n)^3s_2w_4^2)}{(1+n)^2(-1-n+2n^2)w_2w_4\Pi _1}}\right) }{\sqrt{\frac{(-1+n)(1+n)^2w_2w_4^2}{(-1+n)(1+2n)^2w_2^3+16(1+n)^3s_2w_4^2}}}\right] ^{\frac{1}{2n}}\nonumber \\ & \times e^{i(t \omega +\theta -\nu _1 x-\nu _2 y-\nu _3 z)}, \quad q_0=\frac{q_2^2}{4q_4} {,~\frac{n^2((-1+n)(1+2n)^2w_2^3+16(1+n)^3s_2w_4^2)}{(1+n)^2(-1-n+2n^2)w_2w_4\Pi _1}0.} \end{aligned}$$
(18)
The next singular periodic solution is then elevated
$$\begin{aligned} R(x,y,z,t)= & \frac{1}{4}~\left[ -\frac{(1+2n)~w_2}{(1+n)~w_4}+\frac{\cot \left[ \frac{1}{2}~(\eta _1~x+\eta _2~y+\eta _3~z-\gamma ~t)~\sqrt{\frac{n^2~((-1+n)~(1+2n)^2~w_2^3+16~(1+n)^3~s_2~w_4^2)}{(1+n)^2~(-1-n+2~n^2)~w_2~w_4~\Pi _1}}\right] }{\sqrt{-\frac{(-1+n)~(1+n)^2~w_2~w_4^2}{(-1+n)~(1+2n)^2~w_2^3+16~(1+n)^3~s_2~w_4^2}}}\right] ^{\frac{1}{2n}}\nonumber \\ & \times e^{i(t \omega +\theta -\nu _1 x-\nu _2 y-\nu _3 z)},~q_0=\frac{q_2^2}{4~q_4} {,~\frac{n^2~((-1+n)~(1+2n)^2~w_2^3+16~(1+n)^3~s_2~w_4^2)}{(1+n)^2~(-1-n+2~n^2)~w_2~w_4~\Pi _1}>0}\nonumber \\ & {,~\frac{(-1+n)~(1+n)^2~w_2~w_4^2}{(-1+n)~(1+2n)^2~w_2^3+16~(1+n)^3~s_2~w_4^2}
(19)
The next Jacobi elliptic solutions can then be elevated
$$\begin{aligned} R(x,y,z,t)= & \frac{1}{8}~\left[ -~\frac{2~(1+2~n)~w_2}{(1+n)~w_4}+\right. \nonumber \\ & \left. \frac{\sqrt{2}~ j_1}{{{\,\textrm{cn}\,}}\left[ \frac{(\eta _1~x+\eta _2~y+\eta _3~z-\gamma ~t)~\sqrt{\frac{n^2~\left( (-1+n)~(1+2n)^2~w_2^3+16~(1+n)^3~s_2~w_4^2\right) }{(1+n)^2~(-1-n+2~n^2)~(-1+2p^2)~w_2~w_4~\Pi _1}}}{\sqrt{2}},p\right] ~\sqrt{\frac{(-1+n)~(1+n)^2~p^2~w_2~w_4^2~j_1}{(-1+2p^2)~\left( (-1+n)~(1+2n)^2~w_2^3+16~(1+n)^3~s_2~w_4^2\right) }}}\right] ^{\frac{1}{2n}}\nonumber \\ & \times e^{i(t \omega +\theta -\nu _1 x-\nu _2 y-\nu _3 z)},~q_0=\frac{q_2^2~p^2~(1-p^2)}{q_4~(2p^2-1)^2} {,~\frac{n^2~\left( (-1+n)~(1+2n)^2~w_2^3+16~(1+n)^3~s_2~w_4^2\right) }{(1+n)^2~(-1-n+2~n^2)~(-1+2p^2)~w_2~w_4~\Pi _1}>0}\nonumber \\ & {,~\frac{(-1+n)~(1+n)^2~p^2~w_2~w_4^2~j_1}{(-1+2p^2)~\left( (-1+n)~(1+2n)^2~w_2^3+16~(1+n)^3~s_2~w_4^2\right) }>0.} \end{aligned}$$
(20)
$$\begin{aligned} R(x,y,z,t)= & \frac{1}{8}~\left[ -\frac{2~(1+2~n)~w_2}{(1+n)~w_4}+\frac{j_1}{{{\,\textrm{dn}\,}}\left[ \frac{(\eta _1~x+\eta _2~y+\eta _3~z-\gamma ~t)~\sqrt{-\frac{n^2~((-1+n)~(1+2n)^2~w_2^3+16~(1+n)^3~s_2~w_4^2)}{(1+n)^2~(-1-n+2~n^2)~(-2+p^2)~w_2~w_4~\Pi _1}}}{\sqrt{2}},p\right] }\right. \nonumber \\ & \left. \sqrt{-\frac{(-1+n)^2~(1+n)^4~(1+2n)~p^2~w_2^2~w_4^3~j_1^2~\Pi _1}{n^2~(-2+p^2)((-1+n)~(1+2n)^2~w_2^3+16~(1+n)^3~s_2~w_4^2)^2}}\right] ^{\frac{1}{2n}}\nonumber \\ & \times e^{i(t \omega +\theta -\nu _1 x-\nu _2 y-\nu _3 z)},~q_0=\frac{q_2^2~(1-p^2)}{q_4~(2-p^2)^2}\nonumber \\ & {,~\frac{n^2~((-1+n)~(1+2n)^2~w_2^3+16~(1+n)^3~s_2~w_4^2)}{(1+n)^2~(-1-n+2~n^2)~(-2+p^2)~w_2~w_4~\Pi _1}
(21)
$$\begin{aligned} R(x,y,z,t)= & \frac{1}{8}~\left[ -\frac{2~(1+2~n)~w_2}{(1+n)~w_4}+\frac{\sqrt{2}~j_1}{{{\,\textrm{sn}\,}}\left[ \frac{(\eta _1~x+\eta _2~y+\eta _3~z-\gamma ~t)~\sqrt{-\frac{n^2~((-1+n)~(1+2n)^2~w_2^3+16~(1+n)^3~s_2~w_4^2)}{(1+n)^2~(-1-n+2~n^2)~(1+p^2)~w_2~w_4~\Pi _1}}}{\sqrt{2}},p\right] }\right. \nonumber \\ & \left. \sqrt{\frac{(-1+n)~(1+n)^2~p^2~w_2~w_4^2~j_1^2}{(1+p^2)((-1+n)~(1+2n)^2~w_2^3+16~(1+n)^3~s_2~w_4^2)}}\right] ^{\frac{1}{2n}}\nonumber \\ & \times e^{i(t \omega +\theta -\nu _1 x-\nu _2 y-\nu _3 z)},~q_0=\frac{q_2^2~p^2}{q_4~(p^2+1)^2}\nonumber \\ & {,~\frac{n^2~((-1+n)~(1+2n)^2~w_2^3+16~(1+n)^3~s_2~w_4^2)}{(1+n)^2~(-1-n+2~n^2)~(1+p^2)~w_2~w_4~\Pi _1}0} \end{aligned}$$
(22)
Result(2)
$$j_1=0,~q_4=\frac{-4~n^2~w_4~h_1^2}{(1+2n)~\Pi _1},~h_0=\frac{-(1+2n)~w_2}{4~(1+n)~w_4},~q_2=\frac{q_4~(s_2+2~n~s_2+4~w_4~h_0^3-4~n~w_4~h_0^3}{2~(-1+n)~w_4~h_0~h_1^2}.$$
The next dark soliton solution is then elevated
$$\begin{aligned} R(x,y,z,t)= & \left[ \frac{-(1+2n)~w_2}{4~(1+n)~w_4}+\sqrt{\frac{(1+n)~\left( (s_2+2~n~s_2-\frac{(1+2n)^3~w_2^3}{16~(1+n)^3~w_4^2}+\frac{n~(1+2n)^3~w_2^3}{16~(1+n)^3~w_4^2}\right) }{(-1+n)~(1+2n)~w_2}} \right. \nonumber \\ & \left. \tanh \left( 2~(\eta _1~x+\eta _2~y+\eta _3~z-\gamma ~t)~\sqrt{-\frac{n^2~(1+n)~\left( s_2+2~n~s_2-\frac{(1+2n)^3~w_2~3}{16~(1+n)^3~w_4^2}+\frac{n~(1+2n)^3~w_2^3}{16~(1+n)^3~w_4^2}\right) ~w_4}{(-1+n)~(1+2n)~w_2~\Pi _1}}\right) \right] ^{\frac{1}{2n}} \nonumber \\ & \times e^{i(t \omega +\theta -\nu _1 x-\nu _2 y-\nu _3 z)},~q_0=\frac{q_2^2}{4~q_4} {,~\frac{(1+n)~\left( (s_2+2~n~s_2-\frac{(1+2n)^3~w_2^3}{16~(1+n)^3~w_4^2}+\frac{n~(1+2n)^3~w_2^3}{16~(1+n)^3~w_4^2}\right) }{(-1+n)~(1+2n)~w_2}>0}\nonumber \\ & \quad {,~\frac{n^2~(1+n)~\left( s_2+2~n~s_2-\frac{(1+2n)^3~w_2~3}{16~(1+n)^3~w_4^2}+\frac{n~(1+2n)^3~w_2^3}{16~(1+n)^3~w_4^2}\right) ~w_4}{(-1+n)~(1+2n)~w_2~\Pi _1}
(23)
The next singular periodic solution is then elevated
$$\begin{aligned} R(x,y,z,t)= & \left[ \frac{-(1+2n)~w_2}{4~(1+n)~w_4}+\sqrt{-\frac{(1+n)~\left( (s_2+2~n~s_2-\frac{(1+2n)^3~w_2^3}{16~(1+n)^3~w_4^2}+\frac{n~(1+2n)^3~w_2^3}{16~(1+n)^3~w_4^2}\right) }{(-1+n)~(1+2n)~w_2}} \right. \nonumber \\ & \left. \tan \left( 2~(\eta _1~x+\eta _2~y+\eta _3~z-\gamma ~t)~\sqrt{\frac{n^2~(1+n)~\left( s_2+2~n~s_2-\frac{(1+2n)^3~w_2~3}{16~(1+n)^3~w_4^2}+\frac{n~(1+2n)^3~w_2^3}{16~(1+n)^3~w_4^2}\right) ~w_4}{(-1+n)~(1+2n)~w_2~\Pi _1}}\right) \right] ^{\frac{1}{2n}} \nonumber \\ & \times e^{i(t \omega +\theta -\nu _1 x-\nu _2 y-\nu _3 z)},~q_0=\frac{q_2^2}{4~q_4}{,~\frac{(1+n)~\left( (s_2+2~n~s_2-\frac{(1+2n)^3~w_2^3}{16~(1+n)^3~w_4^2}+\frac{n~(1+2n)^3~w_2^3}{16~(1+n)^3~w_4^2}\right) }{(-1+n)~(1+2n)~w_2}0.} \end{aligned}$$
(24)
The next Jacobi elliptic solutions can then be elevated
$$\begin{aligned} R(x,y,z,t)= & \left[ \frac{-(1+2n)~w_2}{4~(1+n)~w_4}+\sqrt{2}~{{\,\textrm{cn}\,}}\left[ 2~\sqrt{2}~(\eta _1~x+\eta _2~y+\eta _3~z-\gamma ~t)\right. \right. \nonumber \\ & \left. \left. \sqrt{\frac{n^2~(1+n)~\left( s_2+2~n~s_2-\frac{(1+2n)^3~w_2^3}{16~(1+n)^3~w_4^2}+\frac{n~(1+2n)^3~w_2^3}{16~(1+n)^3~w_4^2}\right) ~w_4}{(-1+n)~(1+2~n)^2~(-1+2~p^2)~w_2~\Pi _1}},p\right] \right. \nonumber \\ & \left. \sqrt{\frac{(1+n)~p^2~\left( (s_2+2~n~s_2-\frac{(1+2n)^3~w_2^3}{16~(1+n)^3~w_4^2}+\frac{n~(1+2n)^3~w_2^3}{16~(1+n)^3~w_4^2}\right) }{(-1+n)~(1+2n)~(-1+2p^2)~w_2~h_1^2}}~h_1 \right] ^{\frac{1}{2n}} \nonumber \\ & \times e^{i(t \omega +\theta -\nu _1 x-\nu _2 y-\nu _3 z)}, ~q_0=\frac{q_2^2~p^2~(1-p^2)}{q_4~(2p^2-1)^2}{,~\frac{n^2~(1+n)~\left( s_2+2~n~s_2-\frac{(1+2n)^3~w_2^3}{16~(1+n)^3~w_4^2}+\frac{n~(1+2n)^3~w_2^3}{16~(1+n)^3~w_4^2}\right) ~w_4}{(-1+n)~(1+2~n)^2~(-1+2~p^2)~w_2~\Pi _1}>0}\nonumber \\ & {,~\frac{(1+n)~p^2~\left( (s_2+2~n~s_2-\frac{(1+2n)^3~w_2^3}{16~(1+n)^3~w_4^2}+\frac{n~(1+2n)^3~w_2^3}{16~(1+n)^3~w_4^2}\right) }{(-1+n)~(1+2n)~(-1+2p^2)~w_2~h_1^2}>0.} \end{aligned}$$
(25)
$$\begin{aligned} R(x,y,z,t)= & \left[ \frac{-(1+2n)~w_2}{4~(1+n)~w_4}+\frac{1}{2}~{{\,\textrm{dn}\,}}\left[ 2~\sqrt{2}~(\eta _1~x+\eta _2~y+\eta _3~z-\gamma ~t)\right. \right. \nonumber \\ & \left. \left. \sqrt{\frac{n^2~(1+n)~\left( s_2+2~n~s_2-\frac{(1+2n)^3~w_2^3}{16~(1+n)^3~w_4^2}+\frac{n~(1+2n)^3~w_2^3}{16~(1+n)^3~w_4^2}\right) ~w_4}{(-1+n)~(1+2~n)^2~(2-p^2)~w_2~\Pi _1}},p\right] \right. \nonumber \\ & \left. \sqrt{\frac{(1+2n)~p^2~\Pi _1}{n^2~(2-p^2)~w_4~h_1^2}}~h_1\right] ^{\frac{1}{2n}} \nonumber \\ & \times e^{i(t \omega +\theta -\nu _1 x-\nu _2 y-\nu _3 z)}, ~q_0=\frac{q_2^2~(1-p^2)}{q_4~(2-p^2)^2} {,~\frac{n^2~(1+n)~\left( s_2+2~n~s_2-\frac{(1+2n)^3~w_2^3}{16~(1+n)^3~w_4^2} +\frac{n~(1+2n)^3~w_2^3}{16~(1+n)^3~w_4^2}\right) ~w_4}{(-1+n)~(1+2~n)^2~(2-p^2)~w_2~\Pi _1}>0}\nonumber \\ & {\frac{(1+2n)~p^2~\Pi _1}{n^2~(2-p^2)~w_4~h_1^2}>0} \end{aligned}$$
(26)
$$\begin{aligned} R(x,y,z,t)= & \left[ \frac{-(1+2n)~w_2}{4~(1+n)~w_4}+\sqrt{2}~{{\,\textrm{sn}\,}}\left[ 2~\sqrt{2}~(\eta _1~x+\eta _2~y+\eta _3~z-\gamma ~t)\right. \right. \nonumber \\ & \left. \left. \sqrt{\frac{-n^2~(1+n)~\left( s_2+2~n~s_2-\frac{(1+2n)^3~w_2^3}{16~(1+n)^3~w_4^2}+\frac{n~(1+2n)^3~w_2^3}{16~(1+n)^3~w_4^2}\right) ~w_4}{(-1+n)~(1+2~n)^2~(1+p^2)~w_2~\Pi _1}},p\right] \right. \nonumber \\ & \left. \sqrt{\frac{(1+n)~p^2~\left( (s_2+2~n~s_2-\frac{(1+2n)^3~w_2^3}{16~(1+n)^3~w_4^2}+\frac{n~(1+2n)^3~w_2^3}{16~(1+n)^3~w_4^2} \right) }{(-1+n)~(1+2n)~(1+p^2)~w_2~h_1^2}}~h_1\right] ^{\frac{1}{2n}} \nonumber \\ & \times e^{i(t \omega +\theta -\nu _1 x-\nu _2 y-\nu _3 z)},~q_0=\frac{q_2^2~p^2}{q_4~(p^2+1)^2} {,~\frac{n^2~(1+n)~\left( s_2+2~n~s_2-\frac{(1+2n)^3~w_2^3}{16~(1+n)^3~w_4^2}+\frac{n~(1+2n)^3~w_2^3}{16~(1+n)^3~w_4^2}\right) ~w_4}{(-1+n)~(1+2~n)^2~(1+p^2)~w_2~\Pi _1}0.} \end{aligned}$$
(27)
Case 3. \(q_2=q_4=0\), \(q_0\ne 0\), \(q_1\ne 0\), \(q_3>0.\)
Result(1)
$$q_0=\frac{-4n^2~w_4~j_1^2}{(1+2n)~\Pi _1},~ q_1=\frac{4~q_0~h_0}{j_1}-\frac{4n^2~w_2~j_1}{(1+n)~\Pi _1},~ q_3=\frac{h_0^2~(-3~q_1~j_1+4~q_0~h_0)}{j_1^3}+\frac{4n^2~s_2}{(-1+n)~j_1~\Pi _1},$$
$$h_0=\frac{1}{12}~\left( \frac{6-3(1+2n)~w_2}{(1+n)~c_4}+\sqrt{\frac{\left( -\frac{3}{1+n}\right) ^2~w_2^2+24(1+2n)~w_4~(\omega -\Pi _2 )}{w_4^2}}\right) .$$
The next Weierstrass elliptic doubly periodic function is elevated for Eq. (1)
$$\begin{aligned} R(x,y,z,t)= & \left[ \frac{1}{12}~\left( \frac{-3~(1+2n)~w_2}{(1+n)~w_4}+\tau \right) +j_1~/~\wp \left[ \frac{1}{12\sqrt{3}}~(\eta _1~x+\eta _2~y+\eta _3~z-\gamma ~t)~\sqrt{\frac{n^2}{j_1~\Pi _1}~\delta }\right. \right. \nonumber \\ & \left. \left. ,~\{\left( 576~w_4~j_1^2~\tau \right) ~/~((1+2n)~\delta ~)~,~(1728~w_4~j_1^2)~/~((1+2n)~\delta ~)\}~\right] +\right. \nonumber \\ & \left. h_1~ \wp \left[ \frac{1}{12\sqrt{3}}~(\eta _1~x+\eta _2~y+\eta _3~z-\gamma ~t)~\sqrt{\frac{n^2}{j_1~\Pi _1}~\delta }~,\right. \right. \nonumber \\ & \left. \left. \{\left( 576~w_4~j_1^2~\tau \right) ~/~((1+2n)~\delta ~)~,~(1728~w_4~j_1^2)~/~((1+2n)~\delta ~)\}~\right] \right] ^{\frac{1}{2n}}\nonumber \\ & \times e^{i(t \omega +\theta -\nu _1 x-\nu _2 y-\nu _3 z)}, q_0\ne 0, ~q_1\ne 0{,~\Pi _1>0.}, \end{aligned}$$
(28)
where
$$\tau = \sqrt{\frac{\left( 6-\frac{3}{1+n}\right) ^2~w_2^2+24(1+2n)~w_4~(\omega -\Pi _2 )}{w_4^2}}$$
$$\delta = \left( \frac{432~s_2}{-1+n}+\frac{1}{(1+n)^3~(1+2n)~w_4^2}~\left( -3~(1+2n)~w_2+(1+n)~w_4~\tau \right) ^2~(3~(1+2n)~w_2+2~(1+n)~w_4~\tau )~\right) .$$
Case 4. \(q_0=q_1=q_2=0\)
Result(1)
$$\begin{aligned} Q&= (1+n-2n^2)^3~w_2^3 \\&\quad +8\left( -4~(-1+n)^2~(1+n)^3~(1+2n)~s_2~w_4^2\right. \\&\quad \left. +\sqrt{(-1+n)^4~(1+n)^3~(1+2n)^2~s_2~w_4^2((-1+n)~(1+2n)^2~w_2^3+16~(1+n)^3~s_2~w_4^2)} \right) . \end{aligned}$$
$$\begin{aligned} h_0= & (w_2^2+2~n~w_2^2-3~n^2~w_2^2-4~n^3~w_2^2+4~n^4~w_2^2\\ & +w_2~Q^{1/3}+n~w_2~Q^{1/3}-2~n^2~w_2~Q^{1/3}+\frac{Q^{2/3}}{8~(-1+n)~(1+n)~w_4~Q^{1/3}}, \end{aligned}$$
$$j_1=0,~q_4=-\frac{4~n^2~w_4~h_1^2}{(1+2n)~\Pi _1}, q_3=-\frac{q_4~(s_2+2~n~s_2+4~w_4~h_0^3-4~n~w_4~h_0^3)}{3~(-1+n)~w_4~h_0^2~h_1}.$$
The next rational solution is elevated
$$\begin{aligned} R(x,y,z,t)= & \left[ \frac{A}{-8(1-n^2)w_4 Q^{1/3}} \right. \nonumber \\ & \left. + \frac{1}{12288 (1+2n) A^2 \Pi _1 \left( \frac{-8(1+n)n^2 Q^{1/3} (s_2(1+2n)-A)^3}{(1-n^2)^2} + \frac{n A^3}{128(1-n^2)^3 w_4^2 Q} \right) (\eta _1 x+\eta _2 y+\eta _3 z-\gamma t)^2} + \frac{16 n^2 w_4 h_1^2}{\Pi _1(1+2n)} \right] ^{\frac{1}{2n}}\nonumber \\ & \times e^{i(t \omega +\theta -\nu _1 x-\nu _2 y-\nu _3 z)},~q_4 \ne 0 {,(-1+n)^4~(1+n)^3~(1+2n)^2~ s_2~w_4^2((-1+n)~(1+2n)^2~w_2^3+16~(1+n)^3~s_2~w_4^2)>0}. \end{aligned}$$
(29)
The next exponential functions can be elevated
$$\begin{aligned} R(x,y,z,t)= & \left[ 3 (-1+n) \left( A\right) ^3+2 e^{\frac{64 (-1+n) n^2 (1+n)^2 w_4^2 Q^{2/3} \left( s_2+2 n~ s_2-\frac{\left( A\right) ^3}{B}\right) ~ s_1~ (\eta _1 x+\eta _2 y+\eta _3 z-\gamma t)}{3 (1+2 n)~ \left( A\right) ^2 ~\Pi _1 \sqrt{\frac{n^2~ w_4 ~s_1^2}{\Pi _1+2 n ~\Pi _1}}}} \left( 128 \left( 1-n^2\right) ^3~ s_2 ~w_4^2~Q+\right. \right. \nonumber \\ & \left. \left. n ~\left( 1-n^2\right) ^3~ s_2~ w_4^2 ~Q-\left( A\right) ^3+n~ \left( A\right) ^3\right) /\left( 24 (-1+n)^2~ (1+n) ~w_4~ Q^{1/3} ~\left( A\right) ^2 \right) \right] ^{\frac{1}{2n}} \nonumber \\ & \times e^{i(t \omega +\theta -\nu _1 x-\nu _2 y-\nu _3 z)},~q_4
(30)
where:
$$A = w_2^2~(1 + 2n – 3n^2 – 4n^3 + 4n^4) + w_2 ~Q^{1/3}~(1 + n – 2n^2) + Q^{2/3},$$
$$\begin{aligned} B&= 128(1 – n^2)^3~ w_4^2 \left( -(1 + n – 2n^2)^3 ~w_2^3 + 32(-1 + n)^2~ (1 + n)^3 ~(1 + 2n)~ s_2~ w_4^2 \right. \\&\quad \left. – 8 \sqrt{(-1 + n)^4~ (1 + n)^3 ~(1 + 2n)^2~ s_2~ w_4^2~ \left( (-1 + n)~(1 + 2n)^2~ w_2^3 + 16(1 + n)^3 ~s_2~ w_4^2 \right) } \right) . \end{aligned}$$
Case 5. \(q_3=q_4=0\)
Result(1)
$$h_1=0,~q_0=-\frac{4 n^2~ w_4~ j_1^2}{(1+2 n) ~\Pi _1},~q_2=\frac{n^2~ \left( (1+2 n)^2~ w_2^3+\frac{16 (1+n)^3~ s_2~ w_4^2}{-1+n}\right) }{2 (1+n)^2 ~(1+2 n)~ w_2~ w_4~\Pi _1},~h_0=-\frac{(1+2 n)~ w_2}{4 (1+n)~ w_4}.$$
The next singular periodic solution is elevated
$$\begin{aligned} R(x,y,z,t)= & \left[ \frac{1}{4}~ \left( -\frac{(1+2 n)~ w_2}{(1+n)~ w_4}+\frac{\csc \left( \frac{(\eta _1 x+\eta _2 y+\eta _3 z-\gamma t) ~\sqrt{-\frac{n^2 \left( (1+2 n)^2~ w_2^3+\frac{16 (1+n)^3~s_2~ w_4^2}{-1+n}\right) }{(1+n)^2 ~(1+2 n)~ w_2~ w_4 ~\Pi _1}}}{\sqrt{2}}\right) }{\sqrt{\frac{(-1+n)~ (1+n)^2 ~w_2 ~w_4^2}{\left( -2-6 n+8 n^3\right) ~ w_2^3+32 (1+n)^3 ~s_2 ~w_4^2}}}\right) \right] ^{\frac{1}{2n}} \nonumber \\ & \times e^{i(t \omega +\theta -\nu _1 x-\nu _2 y-\nu _3 z)},~q_1=0 {,~\frac{n^2 \left( (1+2 n)^2~ w_2^3+\frac{16 (1+n)^3~s_2~ w_4^2}{-1+n}\right) }{(1+n)^2 ~(1+2 n)~ w_2~ w_4 ~\Pi _1}0} \end{aligned}$$
(31)
The next singular soliton is elevated
$$\begin{aligned} R(x,y,z,t)= & \left[ \frac{1}{4} ~\left( -\frac{(1+2 n)~ w_2}{(1+n)~ w_4}+\frac{\sqrt{2} {{\,\textrm{csch}\,}}\left( \frac{(\eta _1 x+\eta _2 y+\eta _3 z-\gamma t)~ \sqrt{\frac{n^2 ~\left( (1+2 n)^2~ w_2^3+\frac{16 (1+n)^3~ s_2~ w_4^2}{-1+n}\right) }{(1+n)^2~ (1+2 n)~ w_2~ w_4 ~\Pi _1}}}{\sqrt{2}}\right] }{\sqrt{-\frac{(1+n)^2~w_2~ w_4^2 }{(1+2 n)^2 ~w_2^3+\frac{16 (1+n)^3 ~s_2 w_4^2}{-1+n}}}}\right) \right] ^{\frac{1}{2n}} \nonumber \\ & \times e^{i(t \omega +\theta -\nu _1 x-\nu _2 y-\nu _3 z)},~q_1=0{,~\frac{n^2 ~\left( (1+2 n)^2~ w_2^3+\frac{16 (1+n)^3~ s_2~ w_4^2}{-1+n}\right) }{(1+n)^2~ (1+2 n)~ w_2~ w_4 ~\Pi _1}>0} {,~\frac{(1+n)^2~w_2~ w_4^2 }{(1+2 n)^2 ~w_2^3+\frac{16 (1+n)^3 ~s_2 w_4^2}{-1+n}}
(32)
Case 6. \(q_0=q_1=0, ~q_4>0\)
Result(1)
$$j_1=0, h_0=\frac{h_1 ~\left( 4 n^2~ w_2~ h_1+q_3 ~\Pi _1+n~ q_3 ~\Pi _1\right) }{4 (1+n) ~q_4~ \Pi _1}, q_2=\frac{4 n^2~ \omega ~ h_1^2-6 q_4 ~h_0^2~ \Pi _1+3 q_3 ~h_0~ h_1~ \Pi _1-4 n^2~ h_1^2 ~\Pi _2}{h_1^2~ \Pi _1},$$
$$q_4=-\frac{4 n^2 ~w_4~ h_1^2}{(1+2 n)~ \Pi _1},~q_3=2\sqrt{q_2~ q_4}.$$
The next singular periodic solution is elevated The next dark soliton solution is elevated
$$\begin{aligned} R(x,y,z,t)= & \left[ \frac{1}{16 n ~\sqrt{w_4} ~\sqrt{q_4}~ \sqrt{\Pi _1}} ~ \sqrt{-1-2 n}~ \left( \frac{4 ~ n ~\sqrt{-1-2 n}~ w_2 ~\sqrt{q_4} \sqrt{\Pi _1}}{(1+n) ~\sqrt{w_4}}+2 q_3 ~\Pi _1+q_4 ~\Pi _1 \right. \right. \nonumber \\ & \left. \left. \sqrt{\frac{24 n^2 ~(1+2 n)~ w_2^2~ q_4+2 (1+n)^2~ w_4 ~(3 q_3^2 ~\Pi _1+32 n^2 ~q_4 (\omega -\Pi _2))}{(1+n)^2~ w_4~ q_4^2~ \Pi _1}} \left( 1 \right. \right. \right. \nonumber \\ & \left. \left. \left. +\tanh \left( \frac{(\eta _1 x+\eta _2 y+\eta _3 z-\gamma t)~ \sqrt{\frac{\frac{12 n^2 ~(1+2 n)~ w_2^2}{(1+n)^2~ w_4}+\frac{3 q_3^2~ \Pi _1}{q_4}+32 n^2~ (\omega -\Pi _2)}{\Pi _1}}}{4 \sqrt{2}}\right) \right) \right) \right] ^{\frac{1}{2n}} \nonumber \\ & \times e^{i(t \omega +\theta -\nu _1 x-\nu _2 y-\nu _3 z)}, ~w_40 {,~n0}\nonumber \\ & {\frac{\frac{12 n^2 ~(1+2 n)~ w_2^2}{(1+n)^2~ w_4}+\frac{3 q_3^2~ \Pi _1}{q_4}+32 n^2~ (\omega -\Pi _2)}{\Pi _1}>0.} \end{aligned}$$
(33)