Optimizing healthcare supply chain capacity planning during disasters using fuzzy AHP and TOPSIS methods

Fuzzy MCDM has been extensively applied across diverse research domains; however, this discussion is particularly dedicated to elucidating the theoretical underpinnings of the suggested approach. Fuzzy set theory becomes instrumental in scenarios where assigning exact performance ratings and weights proves challenging, thereby encapsulating the uncertainty in evaluations. This scenario is commonly classified as fuzzy MCDM. The foundational work by Bellman and Zadeh in 197055 amalgamated fuzzy set theory with MCDM, enhancing the handling of the ambiguity and imprecision typical of human decision processes.

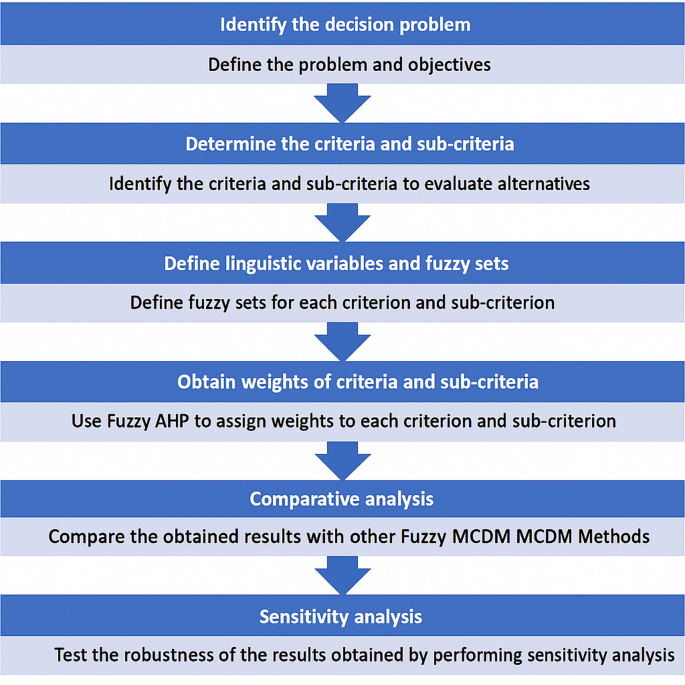
The application of this framework in the management of the capacity of healthcare supply chain networks via Fuzzy AHP and Fuzzy TOPSIS comprises the following steps, described in Fig. 1:

Fig. 1

Steps in the Multi-Criteria Decision-Making Approach for Healthcare Supply Chain Network Capacity Planning under Disaster Conditions.

• Step 1: Formulation of the Decision Problem: Begin by articulating the capacity planning issue within the healthcare supply chain network that requires resolution. It is crucial to delineate the problem comprehensively and define the objectives that must be met.

• Step 2: Establishment of Criteria and Sub-Criteria: Proceed by selecting the criteria and sub-criteria that will guide the evaluation of various alternatives. These should be chosen based on the established framework, which includes elements such as patient demand, availability of resources, cost implications, and quality of care, and should be tailored to address the specific issue at hand.

• Step 3: Development of Linguistic Variables and Fuzzy Sets: For each criterion and sub-criterion, establish linguistic variables and corresponding fuzzy sets. For instance, the criterion “resource availability” may be categorized into fuzzy sets such as “very low,” “low,” “medium,” “high,” and “very high.”

• Step 4: Determination of Weights for Criteria and Sub-Criteria: Ascertain the weights of each criterion and sub-criterion using the Fuzzy AHP. This method involves gathering input from stakeholders to allocate weights, reflecting the relative significance of each criterion and sub-criterion. Fuzzy AHP is particularly useful for accommodating the imprecision and uncertainty characteristic of decision-makers’ assessments.

• Step 5: Alternative Evaluation: Apply Fuzzy TOPSIS to assess the alternatives. Fuzzy TOPSIS evaluates alternatives based on their proximity to the ideal solution, taking into account the uncertainty and ambiguity inherent in the decision-making process.

• Step 6: Sensitivity Analysis: Conduct a sensitivity analysis to examine the stability of the outcomes. This analysis tests how changes in the weights assigned to criteria and sub-criteria influence the final rankings, thereby assessing the robustness of the decision-making process.

Applied MCDM methods under uncertaintyFuzzy sets and fuzzy numbers

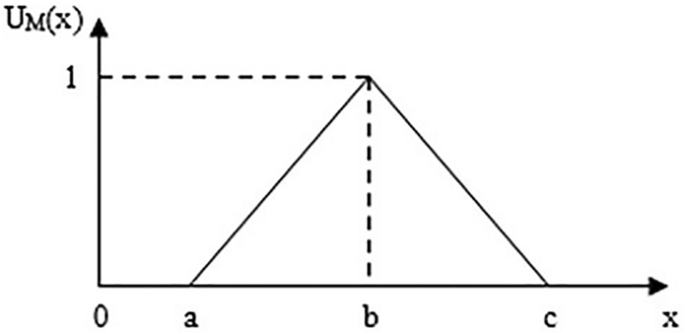
Fuzzy set theory represents an extension of classical set theory, offering a valuable methodological approach for decision-making processes. Initially proposed by Zadeh56, this framework is specifically designed to manage the inherent uncertainties and imprecise characteristics of information. Within academic discourse, various forms of fuzzy numbers, including trapezoidal and triangular types, are utilized to articulate the indeterminacies of parameters pertinent to specific subjects. For the current study, triangular fuzzy numbers (TFNs) are used. Specifically, a triangular fuzzy number \({\bar{e}} (a, b, c)\) is used to account for the fuzziness of57,58. The membership function \(\mu _{\bar{e}}(x)\) of the triangular fuzzy number is described in Fig. 2.

Fig. 2

Triangular fuzzy number (TFN).

$$\begin{aligned} \mu _{\tilde{e}}(x)= {\left\{ \begin{array}{ll}0, & x \le a \\ \frac{x-a}{b=a}, & ac\end{array}\right. } \end{aligned}$$

The fuzzy set theory’s forward, which was applied in this work, is as follows: Let \({\bar{e}}_1 (a_1, b_1, c_1)\) and \({\bar{e}}_2 (a_2, b_2, c_2)\) be two TFNs.

Definition 1 states how to use the vertex technique to determine the distance between them as:

$$\begin{aligned} d\left( \tilde{e}_1, \tilde{e}_2\right) =\sqrt{\frac{1}{3}\left[ \left( a_1-a_2\right) ^2+\left( b_1-b_2\right) ^2+\left( c_1-c_2\right) ^2\right] } \end{aligned}$$

Definition 2 The following are the principal operations on TFNs:

$$\begin{aligned} \begin{aligned}&\tilde{e}_1 \oplus \tilde{e}_2=\left( a_1+a_2, \quad b_1+b_2, \quad c_1+c_2\right) \\&\tilde{e}_1-\tilde{e}_2=\left( a_1-a_2, \quad b_1-b_2, \quad c_1-c_2\right) \\&\tilde{e}_1 \otimes \tilde{e}_2 \approx \left( a_1 \times a_2, \quad b_1 \times b_2, \quad c_1 \times c_2\right) \\&\frac{\tilde{e}_1}{\tilde{e}_2} \approx \left( \frac{a_1}{c_2}, \frac{b_1}{b_2}, \frac{c_1}{a_2}\right) \\&\tilde{e}_1 \otimes k=\left( a_1 \times k, \quad b_1 \times k, \quad c_1 \times k\right) \\&\end{aligned} \end{aligned}$$

Fuzzy AHP

Saaty’s AHP59 is a widely recognized technique for addressing complex decision-making issues that involve multiple criteria, frequently applied in practical situations. It has been demonstrated in various studies to be an effective methodology for optimizing healthcare supply chain networks60,61. Nevertheless, real-world applications often suffer from a lack of precise data, as human judgments tend to be inherently vague. To address the shortcomings of the traditional AHP approach, Van Laarhoven and Pedrycz (1983) introduced the concept of fuzzy AHP, integrating the principles of the Analytic Hierarchy Process with fuzzy logic62. This adaptation permits the use of linguistic evaluations in determining the weights of criteria, thus accommodating ranges rather than precise values. This method facilitates interval judgments over absolute ratings by decision-makers. Balli (2009) highlighted that incorporating fuzziness into AHP helps to capture and articulate imprecise and ambiguous data63.

The literature presents a variety of methodologies for establishing weights within the framework of fuzzy AHP. Bozbura et al.64 offer a succinct overview and comparative analysis of several of these methodologies, each characterized by distinct advantages and Limitations. In this research, the extent analysis method introduced by Chang in 199265, which employs Triangular Fuzzy Numbers (TFNs) to manage fuzzy AHP, is adopted for deriving the fuzzy weights applicable to the selected criteria58,66. Notably, critiques of this method, such as those discussed by Wang67, highlight potential flaws, including the risk of irrationally assigning a zero weight to specific decision criteria and sub-criteria, which may lead to misapplications. The procedural steps of Chang’s extent analysis method for fuzzy AHP are delineated subsequently.

Phase 1: Calculating the fuzzy synthetic extent

$$\begin{aligned} S_i=\sum _{j=1}^m M_{g_i}^j \otimes \left[ \sum _{i=1}^n \sum _{j=1}^m M_{g i}^j\right] ^{-1} \end{aligned}$$

To calculate the sum \(\displaystyle \sum _{j=1}^m M_{g i}^j\), the procedure involves the aggregation of \(\textrm{m}\) values from an extent analysis for a given matrix, which can be articulated as:

$$\begin{aligned} \sum _{j=1}^m M_{g i}^j = \left( \sum _{j=1}^m a_j, \sum _{j=1}^m b_j, \sum _{j=1}^m c_j\right) = (\tilde{a}_i, \tilde{b}_i, \tilde{c}_i) \end{aligned}$$

Furthermore, the computation of \(\displaystyle \left[ \sum _{i=1}^n \sum _{j=1}^m M_{g i}^j\right] ^{-1}\) requires the execution of the fuzzy addition of the matrix elements \(M_{g i}^j\) across the indices \(j = 1, 2, \ldots , m\), performed in such a manner:

$$\begin{aligned} \sum _{i=1}^n \sum _{j=1}^m M_{g i}^j=\left( \sum _{i=1}^n \tilde{a}_i, \quad \sum _{i=1}^n \tilde{b}_i, \quad \sum _{i=1}^n \tilde{c}_i\right) \end{aligned}$$

And then compute the inverse of the vector such that

$$\begin{aligned} \left[ \sum _{i=1}^n \sum _{j=1}^m M_{g_i}^j\right] ^{-1}=\left( \frac{1}{\displaystyle \sum _{i=1}^n \tilde{c}_i}, \quad \frac{1}{\displaystyle \sum _{i=1}^n \tilde{b}_i}, \quad \frac{1}{\displaystyle \sum _{i=1}^n \tilde{a}_i}\right) \end{aligned}$$

Phase 2: Comparing Fuzzy values

The degree of possibility refers to the extent of belief that a particular fuzzy proposition is true. To define the degree of possibility between two different TFNs, use the following function:

$$\begin{aligned} V\left( M_2 \ge M_1\right) =\left\{ \begin{array}{cc} 1 & \text{ if } b_2>b_1 \\ 0 & \text{ if } a_1 \ge c_2 \\ \frac{a_1-c_2}{\left( b_2-c_2\right) -\left( b_1-a_1\right) }, & \text{ Otherwise } \end{array}\right. \end{aligned}$$

Then, compute also \(V\left( M_1 \ge M_2\right)\) to give the complete comparison between \(M_1\) and \(M_2\).

Phase 3: Calculating priority weight

In the case of convex fuzzy numbers CFNs, which is the matter here, the degree of possibility for a CFN M to be greater than k different CFNs means that it is greater than the minimum value of all of them. This can be expressed as:

$$\begin{aligned} V\left( M \ge M_1, M_2, \ldots , M_k\right) =\min _{1\le j\le k} V\left( M \ge M_j\right) . \end{aligned}$$

Let’s denote:

$$\begin{aligned} m\left( P_i\right) =\min \limits _{\begin{array}{c} 1\le i\le n \\ i\ne k \end{array}} V\left( M_i \ge M_k\right) . \end{aligned}$$

Therefore, the weight vector of n elements is denoted by

$$\begin{aligned} W_p =\left( m(P_1), m(P_2), \ldots , m(P_n) \right) ^T. \end{aligned}$$

Phase 4: Normalizing priority weight

The vector obtained by normalizing the last priority weight is a non-fuzzy number called:

$$\begin{aligned} W =\left( W(P_1), W(P_2), \ldots , W(P_n) \right) ^T. \end{aligned}$$

Phase 5: Filling the fuzzy decision matrix

To construct the decision matrix, denoted as \(\tilde{D}\), it is essential to gather assessments from each decision-maker concerning alternatives in relation to criteria. These assessments are to be collected using the fuzzy TOPSIS methodology. The aggregation of these evaluations will be elaborated in the subsequent section. This matrix is given as

$$\begin{aligned} \tilde{D}=\left[ \begin{array}{cccc} \tilde{x}_{11} & \tilde{x}_{12} & \ldots & \tilde{x}_{1 n} \\ \tilde{x}_{21} & \tilde{x}_{22} & \ldots & \tilde{x}_{2 n} \\ \vdots & \vdots & & \ \vdots \\ \tilde{x}_{m 1} & \tilde{x}_{m 2} & \ldots & \tilde{x}_{m n} \end{array}\right] \end{aligned}$$

where,

$$\begin{aligned} \tilde{x}_{i j}=\left( a_{i j}, b_{i j}, c_{i j}\right) \text{, } \quad i=1,2, \ldots , m\quad \text{ and } \quad j=1,2, \ldots , n . \end{aligned}$$

are positive triangular fuzzy numbers.

Phase 6: Normalizing the fuzzy decision matrix

This phase involves converting a fuzzy decision matrix \(\tilde{D}\) into another matrix called \(\bar{R}\). This transformation standardizes the matrix values to a common scale, which is crucial in multi-criteria decision making (MCDM) methods, such as those discussed in the referenced literature by Chen (2000)68.

$$\begin{aligned} \bar{R}=\left[ \bar{r}_{ij}\right] , \quad i=1,2, \ldots , m \quad \text{ and } \quad j=1,2 \ldots , n \end{aligned}$$

such that

$$\begin{aligned} \bar{r}_{j j}=\left( \frac{a_{ij}}{c_j^+}, \frac{b_{i j}}{c_j^+}, \frac{c_{i j}}{c_j^+}\right) \end{aligned}$$

with

$$\begin{aligned} c_j^{+}=\max _{1\le i \le m} c_{ij} \end{aligned}$$

Phase 7: Computing weighted normalized fuzzy decision matrix

Every criterion has a specific weight decided by decision makers. To take them under consideration, let denote the weighted normalized fuzzy decision matrix by

$$\begin{aligned} R=\left[ \bar{r}_{ij} W\right] \quad i=1,2, \ldots , m \quad \text{ and } \quad j=1,2, \ldots , n \end{aligned}$$

and \(W=[\tilde{w}_j]\) is the weighted vector of each criterion that is a TFN such that

$$\begin{aligned} {w}_j= ({w}_{j 1}, {w}_{j 2}, {w}_{j 3}\rangle \end{aligned}$$

Phase 8: Calculating the ranking parameters

These parameters are two, the fuzzy positive ideal solution (FPIS) denoted \(A^*\) and the fuzzy negative ideal solution (IDNS) denoted \(A^-\). Their expressions are taken from68,69 and given by

$$\begin{aligned} \begin{aligned} A^*=\left( R_1^*, R_2^*, R_3^*, \ldots \ldots , R_{n}^*\right) \\ A^{-}=\left( R_1^{-}, R_2^{-}, R_3^{-}, \ldots \ldots , R_n^{-}\right) \end{aligned} \end{aligned}$$

where

$$\begin{aligned} R_j^*=\max _{1\le i \le m}\left\{ r_{ij}\right\} , \quad j=1,2, \ldots , n. \\ R_j^-=\min _{1\le i \le m}\left\{ r_{ij}\right\} , \quad j=1,2, \ldots , n. \end{aligned}$$

Phase 9: Computing the distance to ranking parameters

Referring to68,69, the distance of all alternatives to positive and negative ideal solutions are

$$\begin{aligned} \begin{aligned} d_i^*=\sum _{j=1}^n d_v\left( \tilde{r}_{i j} * R_j^*\right) ; \quad i=1,2, \ldots , m \\ d_i^{-}=\sum _{j=1}^n d_v\left( \tilde{r}_{i j} * R_j^{-}\right) ; \quad i=1,2, \ldots , m \end{aligned} \end{aligned}$$

Phase 10: Ranking alternatives

This is the last phase in the process of decision making. It is concerned with the determination of the closest alternative to the positive ideal solution far from the negative ideal solution by computing the following index:

$$\begin{aligned} CC_i=\frac{d_i^-}{d_i^- + d_i^*}, \qquad i=1,2, \ldots , m. \end{aligned}$$

Fuzzy TOPSIS

The TOPSIS methodology, a technique within the realm of Multiple Criteria Decision Making (MCDM), was initially delineated by Hwang and Yoon in 198170. Subsequently, Chen and Hwang expanded this framework by introducing the fuzzy TOPSIS variant in 199265. Central to the concept of fuzzy TOPSIS is the idea of determining an optimal alternative based on its proximity to the fuzzy positive ideal solution (FPIS) and its remoteness from the fuzzy negative ideal solution (FNIS). The FPIS is characterized by the maximization of advantageous criteria and minimization of detrimental criteria, whereas the FNIS is defined by the converse, maximizing detrimental and minimizing advantageous criteria57,58. The distinctive feature of the fuzzy TOPSIS approach is its utilization of Linguistic variables, represented through fuzzy numbers, to assign weights to criteria and rate alternatives. This adaptation allows for the integration of uncertain or imprecise data into the decision-making process, as evidenced in Table 371,72.

This study employs fuzzy AHP and fuzzy TOPSIS methodologies to ascertain the primary criteria priorities and to sequence the alternatives, respectively. The procedural steps for the fuzzy TOPSIS approach are illustrated in Fig. 1. The algorithm comprises the following stages:

Phase 1: Constitution of a panel of decision-makers assigned to evaluate the alternatives.

Phase 2: Determination of the evaluation criteria.

Phase 3: Adoption of suitable linguistic variables for the ranking of alternatives.

Phase 4: Computation of the cumulative weights for each alternative across all criteria, assuming that the fuzzy evaluations by all decision-makers are represented as triangular fuzzy numbers (TFNs). The calculation of these weights is carried out using the methodology proposed by73.

In this context, for the committee with K experts, the calculations for the minimum, average, and maximum values are given, respectively, by

\(a=\displaystyle \min _k(a_k)\), \(b=\displaystyle \frac{1}{K} \sum _{k=1}^K b_k\), and \(c=\displaystyle \max _k(c_k)\).

These values facilitate the determination of the aggregated fuzzy rating

$$\begin{aligned} R=(a, b, c), \quad k=1,2, \ldots , K \end{aligned}$$

Phase 5: Construct the fuzzy decision matrix as follows:

$$\begin{aligned} \tilde{D}=\left[ \begin{array}{cccc} \tilde{x}_{11} & \tilde{x}_{12} & \ldots \ldots & \tilde{x}_{1 n} \\ \tilde{x}_{21} & \tilde{x}_{22} & \ldots \ldots & \tilde{x}_{2 n} \\ \vdots & \vdots & \vdots & \vdots \\ \tilde{x}_{m 1} & \tilde{x}_{m 2} & \ldots \ldots & \tilde{x}_{m n} \end{array}\right] \end{aligned}$$

(1)

Phase 6: The term ’Z’ denotes the normalized fuzzy decision matrix, as described below.

Phase 7: Formation of the weighted normalized fuzzy decision matrix. This matrix is constructed by integrating the different priority values assigned to each criterion and is outlined as follows:

Phase 8: Execute the calculations necessary to ascertain the fuzzy positive ideal solution (FPIS, A*) and the fuzzy negative ideal solution (FNIS, A-).

Phase 9: Compute the distance from each alternative to both FPIS and FNIS.

Phase 10: Calculate the Closeness Coefficient (CCi) for each alternative. The CCi quantifies the proximity to both FPIS and FNIS, facilitating the ranking of alternatives in descending order, as described by Chen (2000)68.

In recent years, the fuzzy TOPSIS methodology has been employed across a broad spectrum of practical domains.

Expert team set up

In any decision-making process, it is important to have a diverse and knowledgeable team of experts to provide insights and perspectives from different areas of expertise. In the context of evaluating criteria for capacity planning in healthcare supply chain management, the decision-making team may include individuals with a range of backgrounds, such as healthcare providers, supply chain managers, financial analysts, and patient advocates. Each member of the decision-making team contributes a distinct array of skills and experiences, enhancing the capacity to incorporate all pertinent considerations, thereby ensuring that the final decision is both well-informed and robust.

For a comprehensive evaluation of the experts constituting the decision-making team, it is beneficial to consider their respective job titles, years of professional experience, and specific areas of expertise. Such information facilitates a clear comprehension of the team’s composition and its collective capability to influence the decision-making process. Ultimately, the involvement of a diverse cadre of specialists enables the team to render more informed and efficacious decisions, adeptly navigating the complexities and uncertainties inherent in healthcare supply chain capacity planning.

Table 2 provides a description of the experts who participated in the decision-making team.

Table 2 Description of experts participating in the decision-making team.Identify the decision problem

The challenge in capacity planning within healthcare supply chain networks is to guarantee the availability of essential resources–namely personnel, equipment, and materials–to meet the demand of patients in healthcare facilities. This task aims to refine capacity planning decisions, thereby enhancing patient care and increasing operational efficiency across the supply network. It necessitates the assessment and prioritization of various factors influencing these decisions, including patient demand, resource availability, cost implications, care quality, and the preferences of stakeholders. The overarching goal is to optimize the capacity of healthcare facilities to provide exemplary patient care while simultaneously minimizing costs and improving operational effectiveness.

Determine the criteria and sub-criteria

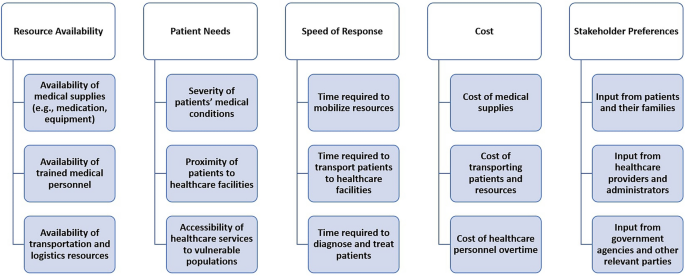
In the domain of healthcare supply chain network capacity planning, the identification and establishment of criteria and sub-criteria for evaluating various alternatives is fundamental. These criteria and sub-criteria form the cornerstone of decision-making processes and are imperative for aligning the selected alternative with the strategic objectives of the healthcare organization and addressing the expectations of its stakeholders. This discussion will concentrate on elucidating the methodology for defining and prioritizing these criteria and sub-criteria, emphasizing their significance and applicability to organizational goals. The Fig. 3 displays the identified criteria and sub-criteria.

Fig. 3

Criteria and Sub-Criteria for Healthcare Supply Chain Network Capacity Planning.

A detailed description of the criteria and sub-criteria is presented below:

1. 1

   Resource Availability : This criterion refers to the availability of resources necessary for providing healthcare services during disaster situations. It takes into account the availability of medical supplies, trained medical personnel, and transportation and logistics resources. The allocation of weight to this criterion reflects its significance in the decision-making framework.

   • Availability of Medical Supplies (e.g., Medication, Equipment): This sub-criterion evaluates the presence of critical medical supplies, including medications, equipment, and personal protective equipment (PPE). The accessibility of these resources is essential for the delivery of efficient healthcare services in emergency scenarios74,75.

   • Availability of trained medical personnel: This sub-criterion considers the availability of trained medical personnel, including doctors, nurses, and other healthcare professionals. The availability of trained medical personnel is essential in providing quality healthcare services during disaster situations76.

   • Availability of transportation and logistics resources: This sub-criterion considers the availability of transportation and logistics resources necessary for delivering medical supplies and personnel to healthcare facilities. It includes factors such as the availability of ambulances, helicopters, and other vehicles, as well as the logistics infrastructure needed to support the delivery of supplies and personnel. The availability of these resources is critical to ensuring that healthcare services can be delivered effectively during disaster situations77.

2. 2

   Patient Needs: This criterion considers the needs of patients who require healthcare services during disaster situations. It takes into account the severity of their medical conditions, their proximity to healthcare facilities, and the accessibility of healthcare services to vulnerable populations. The weighting of this criterion reflects its significance within the decision-making framework.

   • Severity of patients’ medical conditions: This sub-criterion evaluates the severity of patients’ medical conditions, encompassing the intricacy and immediacy of their healthcare requirements. The gravity of medical conditions plays a pivotal role in the distribution of healthcare resources in the context of disaster scenarios78.

   • Proximity of patients to healthcare facilities: This sub-criterion considers the proximity of patients to healthcare facilities. It takes into account factors such as the distance patients must travel to receive medical care, transportation infrastructure, and the location of healthcare facilities. The proximity of patients to healthcare facilities is a crucial factor in determining the allocation of healthcare resources during disaster situations79.

   • Accessibility of healthcare services to vulnerable populations: This sub-criterion considers the accessibility of healthcare services to vulnerable populations, such as the elderly, disabled, and low-income groups. This assessment incorporates variables such as linguistic obstacles, cultural factors, and socio-economic conditions. Ensuring that healthcare services are accessible to vulnerable groups is essential for achieving equitable healthcare access during emergencies and disastrous situations80,81,82.

3. 3

   Speed of Response: This criterion considers the speed of response in delivering healthcare services during disaster situations. This criterion considers the necessary duration for resource mobilization, patient transportation to medical facilities, and the diagnosis and treatment of patients. The emphasis placed on this criterion reflects its significance in the decision-making framework.

   • Time required to mobilize resources: This sub-criterion considers the time required to mobilize healthcare resources, including medical personnel, supplies, and equipment. The faster the resources can be mobilized, the more efficient and effective the response will be to meet the healthcare needs of disaster victims83.

   • Duration for Patient Transfer to Medical Centers: This parameter evaluates the temporal aspect of conveying patients to healthcare institutions. It encompasses the accessibility of transport networks, the geographic distances that patients must navigate, and prevailing traffic dynamics. The faster patients can be transported to healthcare facilities, the higher the chances of survival and recovery84.

   • Time frame for Diagnosis and Treatment: This sub-criterion evaluates the duration necessary for the diagnosis and treatment of patients. It encompasses the accessibility of healthcare staff and medical equipment, as well as the efficacy of the medical processes involved. The faster patients can be diagnosed and treated, the higher the chances of survival and recovery85,86.

4. 4

   Cost: This criterion considers the costs associated with providing healthcare services during disaster situations. It takes into account the cost of medical supplies, the cost of transporting patients and resources, and the cost of healthcare personnel overtime. The significance attributed to this criterion reflects its relative priority within the decision-making framework.

   • Cost of medical supplies: This sub-criterion considers the cost of medical supplies such as medication, medical equipment, and consumables. The cost of these supplies can increase significantly during disaster situations due to shortages or high demand. The significance attributed to this criterion reflects its relative priority within the decision-making framework87.

   • Cost of transporting patients and resources: This sub-criterion considers the cost of transporting patients and resources to and from healthcare facilities. This includes the cost of transportation infrastructure, fuel, and maintenance. The significance attributed to this criterion reflects its relative priority within the decision-making framework88,89.

   • Cost of healthcare personnel overtime: This sub-criterion considers the cost of healthcare personnel overtime. During disaster situations, healthcare personnel may need to work longer hours or be called in for emergency shifts, which can result in higher labor costs. The weight assigned to this sub-criterion indicates its relative importance in the decision-making process86.

5. 5

   The Stakeholder Preferences criterion refers to the input and preferences of stakeholders involved in the healthcare supply chain network during capacity planning under disaster conditions. The significance attributed to this criterion reflects the relative priority of stakeholder preferences within the decision-making framework.

   • Input from patients and their families: This sub-criterion reflects the preferences and needs of patients and their families, such as the type of medical care they require and their preferred healthcare facilities. The significance attributed to this criterion reflects the relative priority of patient and family input in decision-making90,91.

   • Input from healthcare providers and administrators: This sub-criterion refers to the input and preferences of healthcare providers and administrators, including their knowledge and experience in dealing with disaster situations. The significance attributed to this criterion reflects the relative priority of the expertise and input of healthcare professionals and administrators in decision-making92.

   • Input from government agencies and other relevant parties: This sub-criterion reflects the input and preferences of relevant government agencies and other parties involved in disaster response and recovery efforts, such as non-governmental organizations and community groups. The significance attributed to this criterion reflects the relative priority of the input and expertise of external stakeholders in decision-making93.

Define linguistic variables and fuzzy sets

To address the inherent uncertainties in evaluating criteria within healthcare supply chains during disasters, this study establishes linguistic variables and fuzzy sets corresponding to scales of importance in the multi-criteria decision-making framework. This strategy enables the transformation of qualitative evaluations into quantitative data, which is essential for implementing fuzzy MCDM techniques.

The importance levels are expressed through linguistic terms, each linked to distinct triangular fuzzy numbers. These numbers effectively encapsulate the ambiguity and subjective nature of human assessments. A detailed exposition of these linguistic scales and their respective triangular fuzzy scales is delineated in Table 3.

Table 3 Linguistic Terms and the Corresponding Triangular Fuzzy Number.

Fuzzy numbers are utilized within the context of the fuzzy AHP to determine the relative importance of criteria and sub-criteria in the capacity planning of healthcare supply chain networks. The adoption of fuzzy sets in the decision-making process enables the effective handling and interpretation of uncertainties inherent in expert assessments and preferences. This is essential for developing a robust and resilient healthcare supply chain system, particularly in scenarios complicated by disasters.

In subsequent stages, these fuzzy scales will be utilized to develop pairwise comparison matrices, essential for determining the relative significance of the criteria and sub-criteria through fuzzy AHP. The results provide a clear, quantitative framework for decision-makers, facilitating more informed and precise strategic planning in uncertain conditions.

Obtain weights of criteria and sub-criteria

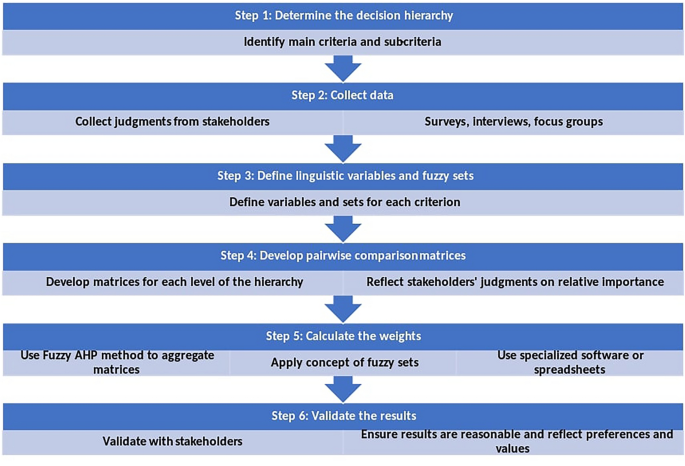
To make effective decisions in healthcare care, it is necessary to follow a structured approach. Figure 4 outlines the six main steps involved in using the Fuzzy AHP to make decisions. The initial phase involves establishing the decision hierarchy by delineating the primary and secondary criteria essential for the decision-making framework. Subsequently, the second phase entails gathering empirical data from relevant stakeholders, such as patients, healthcare providers, and administrators, regarding their assessments of the comparative significance of these criteria and sub-criteria. This can be achieved through surveys, interviews, or focus groups. Next, the third step involves defining linguistic variables and fuzzy sets for each criterion and sub-criterion. For example, “resource availability” can be defined with fuzzy sets such as “very low,” “low,” “medium,” “high,” and “very high.” The fourth phase entails constructing pairwise comparison matrices at each hierarchical level of decision-making, encapsulating stakeholder evaluations regarding the relative significance of both criteria and sub-criteria. Subsequently, the fifth phase involves the computation of weights through the application of the Fuzzy AHP method. This method consolidates the pairwise comparison matrices and integrates the principles of fuzzy sets. This step can be done using specialized software or spreadsheets. Finally, the results must be validated with stakeholders to ensure that they are reasonable and reflect their preferences and values.

Fig. 4

Steps in Fuzzy AHP Decision-Making Process for Healthcare Planning.

The Table 4 meticulously outlines the criteria and sub-criteria identified for strategic capacity planning within healthcare supply chain networks. These elements are fundamental to the decision-making process, guiding healthcare organizations in optimizing their operational strategies and resource allocations. The criteria include essential operational aspects such as resource availability, patient needs, speed of response, cost considerations, and stakeholder preferences. Each criterion within this set is further delineated into narrower sub-criteria, establishing a comprehensive schema for examination.

For each criterion and its associated sub-criteria, specific weights are assigned, reflecting their importance and relevance to the overarching goals of the organization. The assignment of these weights is based on a systematic analysis which considers factors like the frequency of demand for certain resources, the critical nature of certain patient needs, and the potential impact of rapid response capabilities on patient outcomes.

Each criterion within this set is further delineated into narrower sub-criteria, establishing a comprehensive schema for examination. This matrix aids in visually articulating the interdependencies and relative significance of various factors, thus facilitating a more informed decision-making process.

Table 4 Comparison Matrix of Criteria with Weights.

Table 5 provides further granularity by focusing on the sub-criteria within ’Patient Needs’. This table assigns weights to elements such as ’Severity of patients’ medical conditions’, emphasizing their critical impact on decision-making in resource allocation and emergency response planning. This detailed breakdown assists in prioritizing interventions and resources in a manner that is directly aligned with patient-centric outcomes.

Table 5 Fuzzy aggregation matrix for the C2.

Table 6 presents a consolidated analysis through the application of the Fuzzy AHP, computing both local and global weights for each criterion and sub-criterion. This evaluation methodologically underscores the significance of specific sub-criteria, for example, ’Availability of medical supplies’, and elucidates their aggregated effect on overarching strategic decisions. The global weights delineate the comprehensive impact of each criterion on the decision-making framework, facilitating decisions that are both quantitatively grounded and strategically coherent.

Table 6 Calculating of local and global weights of all criteria and sub-criteria using Fuzzy AHP.Evaluation of alternatives

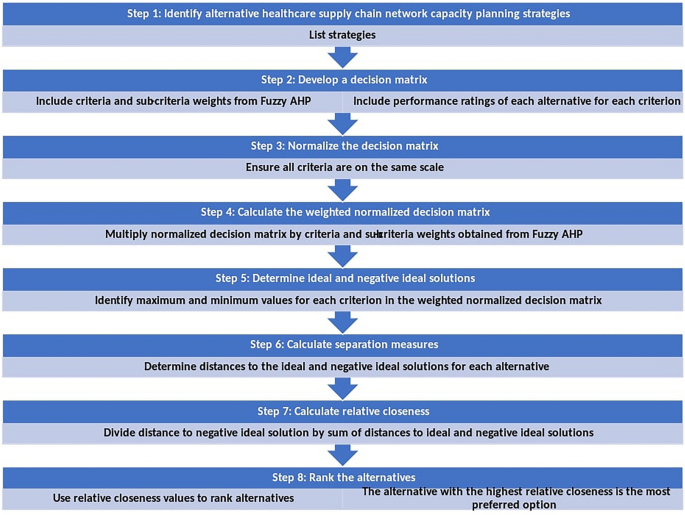
In the domain of healthcare supply chain network capacity planning, adopting a structured methodology is essential. As depicted in Fig. 5, the process encompasses eight critical stages, utilizing the fuzzy TOPSIS method to ascertain the optimal strategy. The initial stage entails the delineation and enumeration of prospective strategies for healthcare supply chain network capacity planning. Subsequently, a decision matrix is constructed, incorporating both the weights of criteria and sub-criteria derived from Fuzzy AHP and the performance scores of each strategy against these criteria. The third phase involves the normalization of the decision matrix to standardize the criteria scales. Following this, the fourth stage requires the calculation of a weighted normalized decision matrix by applying the weights from Fuzzy AHP to the normalized values. The fifth stage is dedicated to identifying the ideal and the negative ideal solutions, which are established by pinpointing the maximal and minimal values for each criterion within the weighted normalized matrix. The sixth stage comprises the computation of separation measures for each strategy, assessing their distances from both the ideal and negative ideal solutions. In the penultimate step, the relative proximity of each strategy to the ideal solution is quantified by dividing the distance to the negative ideal solution by the aggregate distances to both the ideal and negative ideal solutions. The final stage involves ranking the strategies based on their relative closeness indices, with preference given to the strategy that exhibits the highest relative closeness.

Fig. 5

Steps for Evaluating Healthcare Supply Chain Network Capacity Planning Strategies.