CoFe\(_2\)O\(_4\)–-Pr:SrTiO\(_3\) thick film preparation
Cobalt acetate (Co(CH\(_3\)CO\(_2)_2\).4H\(_2\)O, Sigma Aldrich), Iron nitrate (Fe(NO\(_3)_3\).9H\(_2\)O, Sigma Aldrich), Titanium isopropoxide (C\(_{12}\)H\(_{28}\)O\(_4\)Ti, Sigma Aldrich), Praseodymium nitrate hexahydrate (Pr(NO\(_3)_3\).6H\(_2\)O), Acetyl acetone (C\(_5\)H\(_8\)O\(_2\), Sigma Aldrich), Ethylene glycol (C\(_2\)H\(_6\)O\(_2\), Sigma Aldrich), Strontium acetate (C\(_4\)H\(_6\)O\(_4\)Sr, Sigma Aldrich), 2-Methoxy ethanol (2-MOE, Sigma Aldrich) and Diethanolamine (DEA, Sigma Aldrich) were used as the starting materials.
About 0.02 mol of (Co(CH\(_3\)CO\(_2\))\(_2\).4H\(_2\)O and 0.01 mol of (Fe(NO\(_3\))\(_3\).9H\(_2\)O were mixed in 2-MOE and DEA in a round bottomed flask, using an ultra sonicator. Vigorous sonication was performed for 2 h till a uniform mixture of precursor was obtained. This solution was kept in an oil bath at 70\(^\circ\)C and continued heating for 12 h under constant stirring with refluxing in order to avoid evaporation of the solvents. After 12 h, the solution was allowed to dry. The dried powder was then taken for further characterizations.
The Pr doped strontium titanate was synthesized using a sol-gel synthesis route. For this, C\(_{12}\)H\(_{28}\)O\(_4\)Ti was added to C\(_5\)H\(_8\)O\(_2\) in a round bottom (RB) flask at 120\(^\circ\)C under constant stirring. After 30 minutes C\(_2\)H\(_6\)O\(_2\) was added to the solution. At the same time, in another RB, sufficient quantity of C\(_4\)H\(_6\)O\(_4\)Sr and Pr(NO\(_3)_3\).6H\(_2\)O (Sr:Pr= 0.925:0.075) were dissolved in ethylene glycol, C\(_2\)H\(_6\)O\(_2\), and were kept at 120\(^\circ\)C kept under constant stirring. After 1 h of mixing, both these solutions were mixed together and allowed to stir at 120\(^\circ\)C. After 4 h of mixing, 3 ml deionized water was added to the above mixture to form the stable solution of Pr:STO. The solution was then air dried at 100\(^\circ\)C and the obtained powder was ground well, calcined and qualified for ink preparation.
After the phase formation of Pr:STO and CFO were confirmed and powders were qualified, our next aim was to develop a viscous ink out of the developed powder. The solvents chosen here is a binary solvent system consisting of xylene and ethanol, Triton X-100 as dispersant and ethyl cellulose as binder. A screen printable ink usually consists of filler, solvent, binder as well as dispersant. Here, the fillers are the perovskite oxides Pr:STO and CFO. Binary solutions having equal volumes of xylene and ethanol were chosen as solvents in order to facilitate fast curing for the proposed inks.
-
(i)
In the first step, Triton X-100, the dispersant, was dissolved in solvent mixture for 30 min in an ultrasonic bath.
-
(ii)
Respective fillers (Pr:STO and CFO) was added to the solution and stirred continuously for 4 h in a magnetic stirrer.
-
(iii)
Ethyl cellulose (binder) was added and stirred for another 24 h to get a homogenous ink with desired viscosity.
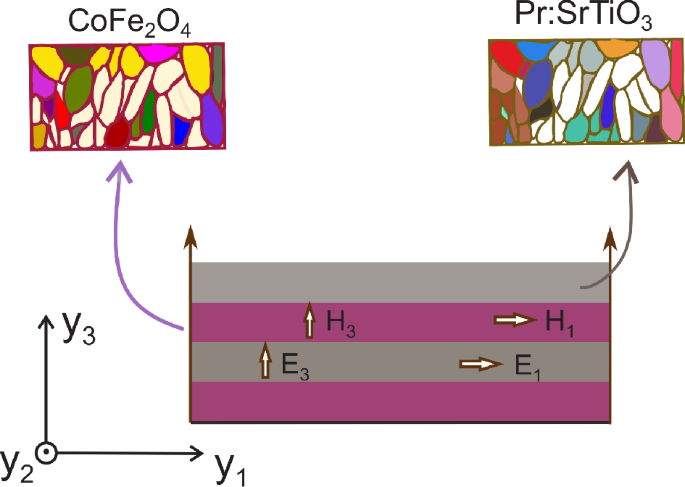
For the production of hybrid ME composites, these inks were screen printed on desired substrates (preferably, Si(100)/SiO\(_2\)/TiO\(_2\)/Pt substrates) one over other and was kept at 100\(^\circ\)C for 24 h in an oven.
Characterization
TG/DTA was performed using a thermo gravimetric analyzer from room temperature upto 1000\(^\circ\)C in oxygen atmosphere (TGA/DTA instruments, Shimadzu, Japan). Phase purity of calcined powder was confirmed using X-ray diffraction technique with \(Cu K\alpha\) radiation (X’Pert PRO diffractometer, PANalytical, Almelo, The Netherlands). High resolution TEM was used for analyzing the particle size of developed CFO powder (FEI Tecnai G2 30S-TWIN, FEI Co., Hillsboro, OR, USA). The rheological behavior of the ink was done using Rheo plus32 rheometer (Anton Paar, Ashland, VA, USA). The screen printing of ink on different substrates were performed using XPRT2 semiautomatic screen-printer (EKRA, Germany). Scanning electron microscopy was used for the microstructural analysis of printed films using JSM 5600LV model (JEOL, Tokyo, Japan). Surface roughness of thick film was estimated with the help of atomic force microscopy (AFM) in tapping mode (Multimode, Bruker, Germany). Magnetic measurements were performed using an oven setup attached to the physical property measurement system (PPMS, Quantum Design, USA). ME measurements were carried out in ac as well as dc magnetic fields. The ac magnetic field was applied with the help of a pair of Helmholtz coils using which, a suitable magnetic field was applied across the sample and the ME output voltage was estimated by recording the induced polarization (P). The working principle is that the electric dipoles inside the sample align themselves with the ac magnetic field, resulting a drop in ac voltage across the sample which is measured via Faraday Effect. Thus it is clear that the apparent output voltage is purely due to the ME coupling effect. For measuring the dc field dependence of ME coupling, a setup consisting of dc electromagnet having bipolar power supply with GPIB integrated gauss meter. Both these fields were applied along the direction of thickness of the printed heterostructure. The data acquisition was performed using LabVIEW software. Now, the electric as well as magnetic inductions in a ME laminate can be expressed as,
$$\begin{aligned} P_i=\dfrac{\partial F}{\partial E_{0i}}&=P_{Si} +\epsilon _0 \sum _j\chi _{ij}^e E_{0j} +\dfrac{1}{\mu _0}\sum _j\alpha _{ij} B_{0j}+\cdots \\ M_i=\dfrac{\partial F}{\partial B_{0i}}&=M_{Si} +\dfrac{1}{\mu _0}\sum _j\chi _{ij}^m B_{0j} +\dfrac{1}{\mu _0}\sum _j\alpha _{ij} E_{0j}+\cdots \end{aligned}$$
From these two equations, it is clear that, there is a component for cross polarization irrespective of spontaneous and induced terms. The linear ME effect is given by, \(\alpha _{ij}=\dfrac{\partial P_i }{\partial B_{0j}}= \mu _0 \dfrac{\partial M_i}{\partial E_{0j}}\) For an isotropic material, \(\alpha ^2=\epsilon _0\mu _0 \chi ^e \chi ^m\). This suggests that, large ME coupling can be observed in materials with large electric and magnetic susceptibility values.
Simulation using homogenization
The equivalent material properties of a periodic multiferroic magnetoelectric composite at equilibrium are determined using a two-scale asymptotic homogenization analysis29. The equivalent ME coupling thus obtained is given by
$$\begin{aligned} & \widetilde{\alpha }_{im}= \frac{1}{\left| Y \right| }\int _Y \Big [ e_{pkl}(\textbf{x,y}) \frac{\partial \Gamma ^{m}_k}{\partial y_l}- \kappa ^{\epsilon H}_{pj}(\textbf{x,y})\frac{\partial \Psi ^{m}}{\partial y_j} \nonumber \\ & -\alpha _{pj}(\textbf{x,y})\Big (\delta _{jm}+ \frac{\partial Q^{m}}{\partial y_{j}} \Big )\Big ] \nonumber \\ & \times \Big (\delta _{ip}+\frac{\partial R^i}{\partial y_p}\Big )\mathrm d Y \end{aligned}$$
(2)
Here R and Q are characteristic electric and magnetic displacements. \(\mathbf {\Gamma },\) and \(\Psi\) are characteristic coupled functions satisfying a set of microscopic equations29. These characteristic functions appear in the microscopic displacement, electric and magnetic field perturbations, viz., \(\mathbf {u^1(x,y)}\), \(\varphi ^1\mathbf {(x,y)}\) and \(\psi ^1\mathbf {(x,y)}\) respectively (given in Supplementary material), due to the microstructure heterogeneity. The spacial derivatives of the macroscopic displacement, electric and magnetic fields viz., \(\mathbf {u^0(x,y)}\), \(\varphi ^0\mathbf {(x,y)}\) and \(\psi ^0\mathbf {(x,y)}\) can bridge the macroscale and the microscale through the characteristic functions mentioned above. \(e_{pkl}\) and \(\kappa _{pj}^{\epsilon H}\) are the piezoelectric coefficient and dielectric permittivity at constant strain \(\epsilon\) and magnetic field vector \(\textbf{H}\) respectively. \(i, j, k, l, \dots = 1,2,3\) are the 3–dimensional coordinate indices, and \(\delta _{ij}\) are the Kronecker delta symbol. Here we assume Einstein convention on summation about repeated indices. (Here the \(\sim\) over Greek or Latin letters represents homogenized values). We consider the ME composite as a heterogeneous body obtained by the translation of microstructure of size Y. For the homogenized ME composite laminate, the physical properties do not depend on \(\textbf{x}\), the global frame of reference. Instead, if the material is heterogeneous, the magneto-electro-mechanical properties effectively depend on \(\textbf{x}\) such that \(\mathbf \kappa ^{\epsilon H} \equiv \mathbf \kappa ^{\epsilon H}(\textbf{x}), ~ \textbf{e}\equiv \textbf{e}(\textbf{x}), \dots\) etc. The material properties \(\mathbf \kappa ^{\epsilon H}\), \(\textbf{e}\), \(\mathbf \alpha\), etc as well as the characteristic functions \(R, Q, \mathbf {\Gamma }\), and \(\Psi\) are Y–periodic functions depending on the microscopic coordinates \(\textbf{y}\).
The equivalence of the average stress and homogenised stress can easily be expressed by applying the average operator \(\langle \centerdot \rangle\) denoting \((\frac{1}{\left| Y \right| }\int _Y \centerdot dY)\), where Y is the domain size. Hence the average fields are computed to be
$$\begin{aligned} \langle \sigma _{ij}\rangle= & \widetilde{C}^{EH}_{ijkl}\Bigg (\frac{\partial u^0_k(\textbf{x})}{\partial x_l}\Bigg ) +\widetilde{e}_{kij}\Bigg (\frac{\partial \varphi ^0(\textbf{x})}{\partial x_k}\Bigg )+\widetilde{e}^{~M}_{kij} \Bigg (\frac{\partial \psi ^0(\textbf{x})}{\partial x_k}\Bigg ) \end{aligned}$$
(3)
$$\begin{aligned} \langle D_{i}\rangle= & \widetilde{e}_{ijk}\Bigg (\frac{\partial u^0_j(\textbf{x})}{\partial x_k}\Bigg )- \widetilde{\kappa }^{\epsilon H}_{ij}\Bigg (\frac{\partial \varphi ^0(\textbf{x})}{\partial x_j}\Bigg )-\widetilde{\alpha }_{ij}\Bigg (\frac{\partial \psi ^0(\textbf{x})}{\partial x_j}\Bigg ) \end{aligned}$$
(4)
$$\begin{aligned} \langle B_{i}\rangle= & \widetilde{e}^{~M}_{ijk}\Bigg (\frac{\partial u^0_j(\textbf{x})}{\partial x_k}\Bigg )- \widetilde{\alpha }_{ji}\Bigg (\frac{\partial \varphi ^0(\textbf{x})}{\partial x_j}\Bigg )-\widetilde{\mu }^{\epsilon E}_{ij} \Bigg (\frac{\partial \psi ^0(\textbf{x})}{\partial x_j}\Bigg ) \end{aligned}$$
(5)
These macroscopic equations (i.e. they do not contain \(\textrm{y}\)) can be computed once the homogenized solution for \(\textbf{u}^0\), \(\varphi ^0\) and \(\psi ^0\) and that of the corresponding fields viz., \(\frac{\partial u^0_j(\textbf{x})}{\partial x_k}\), \(\frac{\partial \varphi ^0(\textbf{x})}{\partial x_j}\) and \(\frac{\partial \psi ^0(\textbf{x})}{\partial x_j}\) are prescribed. This postulate is equally applicable for the case with the microscopic fields and for the microscopic stress, electrical displacement and flux densities.
Both the constituents of the system of 2–2 magnetoelectric composite consisting of layer of FE material (STO) glued into a laminae with a layer of FM material (CFO) are of equal volume. We use, single crystalline data for STO (from Ref. 32) and polycrystalline data for CFO (from Ref. 40).
The numerical implementation is based on the software POSTMAT(material postprocessing) developed by Guedes and Kikuchi39, which is explained in Supplementary material.